如下所示:
a = np.arange(1, 5).reshape(2, 2) b = np.arange(2, 6).reshape(2, 2) c = a * b dot = np.dot(a, b) print(a) print(b) print(c) print(dot)
打印出a
[[1 2]
[3 4]]
打印出b
[[2 3]
[4 5]]
a * b 每个相对位置的数值相乘1*2=2,2*3=6,3*4=12,4*5=20.比较简单,自己脑补一下
[[ 2 6]
[12 20]]
a.dot(b)也可以下成下面的那种形式,看你喜欢了.关键是算法
np.dot(a,b)
[[10 13]
[22 29]]
10=1*2+2*4 a[1][1]*b[1][1]+a[1][2]*b[2][1]
13=1*3+2*5
22=3*2+4*4
29=3*3+4*5 a[2][1]*b[1][2]+a[2][2]*b[2][2]
就这样了,规律自己找~
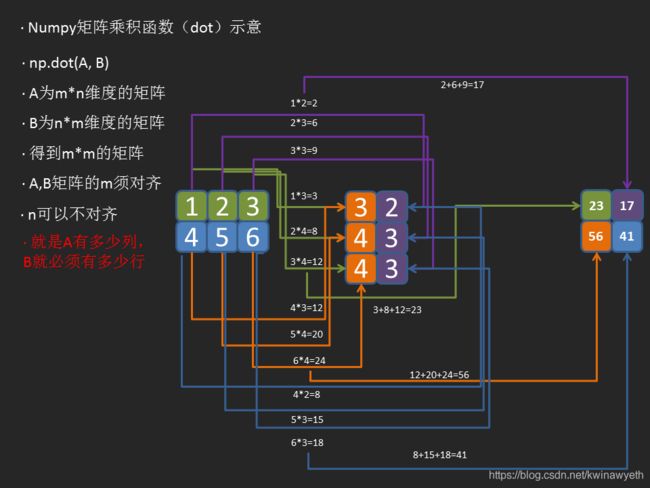
补充:Numpy矩阵乘积函数(dot)运算规则解析
np.dot(A, B)
A为二维m*n的举证,B必须为n*l的矩阵,l两个矩阵的n必须一致,也就是说A有多少列,B就必须有多少行,否则无法运算。结果得到m*l的矩阵
m*l = np.dot(m*n,n*l),m n l指维度,得到m*l的矩阵
运算顺序如下图:
程序演示如下:
import numpy as np A = [[1, 2, 3], [4, 5, 6]] B = [[3, 2], [4, 3], [4, 3]] print(np.dot(A, B))
结果:
[[23 17]
[56 41]]
如果A和B的形状交换会怎么样呢?
import numpy as np A = [[1, 2, 3], [4, 5, 6]] B = [[3, 2], [4, 3], [4, 3]] print(np.dot(B, A))
结果是这样哟!不是说形状一定是变小哟
[[11 16 21]
[16 23 30]
[16 23 30]]
这是A和B的形状不一样:
import numpy as np A = [[1, 2, 3], [4, 5, 6]] B = [[3], [4], [4]] print(np.dot(A, B))
结果如下:
[[23]
[56]]
以上为个人经验,希望能给大家一个参考,也希望大家多多支持脚本之家。如有错误或未考虑完全的地方,望不吝赐教。