夜深人静写算法(一)- 搜索入门
文章目录
- 一、前言
- 二、搜索算法的原理
- 三、深度优先搜索
-
- 1、DFS
- 2、基于DFS的记忆化搜索
- 3、基于DFS的剪枝
- 4、基于DFS的A*(迭代加深,IDA*)
- 四、广度优先搜索
-
- 1、BFS
- 五、搜索题集整理
-
- 1、DFS题集
- 2、IDA*题集
- 3、BFS 题集
- 4、双向BFS 题集
一、前言
回首往事,再来看自己五年前写的这篇文章 《夜深人静写算法(一)- 搜索入门》,发现虽然标题写的是入门,但是还是有很多地方较为晦涩,而且多为文字,图片相对较少,初学者不易理解,这和我当初分享算法的初衷背道而驰。毕竟我不希望很多壮怀激烈的仁人志士因为我的文章放弃了算法这条路。因为,我的愿景是:让天下没有难学的算法。
基于这个原因,我打算重新整理《夜深人静写算法》系列,让同样和我志同道合的人积极投身到这个事业中来,将祖国的算法和技术发扬光大,背靠祖国,面向国际,强我国威,壮我河山!
这次的修订版本会持续连载,并且会从易到难重新整理规划目录,读者可以放心从前往后阅读,如果中途有涉及到一些数学、数据结构、计算机原理方面的知识,我会另外开辟章节进行详细讲解。当然,如果有遇到写的不清楚的地方,也可以给我留言,我会尽我最大的努力把它调整清晰,文章群体主要面向 中小学生以及大学生,毕竟,你们才是国家未来的栋梁之才!
二、搜索算法的原理
- 搜索算法的原理就是枚举。利用计算机的高性能,给出人类制定好的规则,枚举出所有可行的情况,找到可行解或者最优解。
- 比较常见的搜索算法是 深度优先搜索(又叫深度优先遍历) 和 广度优先搜索(又叫广度、宽度优先遍历)。各种图论的算法基本都是依靠这两者进行展开的。
- 深度优先搜索一般用来求可行解,利用剪枝进行优化,在树形结构的图上用处较多;而广度优先搜索一般用来求最优解,配合哈希表进行状态空间的标记,从而避免重复状态的计算;
三、深度优先搜索
1、DFS
1)算法原理
- 深度优先搜索(Depth First Search),是图遍历算法的一种。用一句话概括就是:“一直往下走,走不通回头,换条路再走,直到无路可走”。具体算法描述为:
选择一个起始点 u 作为 当前结点,执行如下操作:
a. 访问 当前结点,并且标记该结点已被访问,然后跳转到 b;
b. 如果存在一个和 当前结点 相邻并且尚未被访问的结点 v,则将 v 设为 当前结点,继续执行 a;
c. 如果不存在这样的 v,则进行回溯,回溯的过程就是回退 当前结点;
- 上述所说的 当前结点 需要用一个栈来维护,每次访问到的结点入栈,回溯的时候出栈(栈是数据结构中线性表的一种,我会另外开辟一个章节来仔细讲解栈的原理和应用)。
- 除了栈,另一种实现深度优先搜索的方式是递归,代码更加简单,相对好理解;
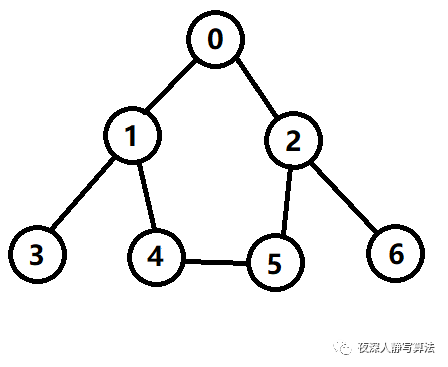
【例题1】给定一个 n 个结点的无向图,要求从 0 号结点出发遍历整个图,求输出整个过程的遍历序列。其中,遍历规则为:
1)如果和 当前结点 相邻的结点已经访问过,则不能再访问;
2)每次从和 当前结点 相邻的结点中寻找一个编号最小的没有访问的结点进行访问;
图三-1
- 如图1所示,对上图以深度优先的方式进行遍历,起点是 0;
- <1> 第一步,当前结点为 0,标记已访问,然后从相邻结点中找到编号最小的且没有访问的结点 1;
- <2> 第二步,当前结点为 1,标记已访问,然后从相邻结点中找到编号最小的且没有访问的结点 3;
- <3> 第三步,当前结点为 3,标记已访问,没有尚未访问的相邻结点,执行回溯,回到结点 1;
- <4> 第四步,当前结点为 1,从相邻结点中找到编号最小的且没有访问的结点 4;
- <5> 第五步,当前结点为 4,标记已访问,然后从相邻结点中找到编号最小的且没有访问的结点 5;
- <6> 第六步,当前结点为 5,标记已访问,然后从相邻结点中找到编号最小的且没有访问的结点 2;
- <7> 第七步,当前结点为 2,标记已访问,然后从相邻结点中找到编号最小的且没有访问的结点 6;
- <8> 第八步,当前结点为 6,标记已访问,没有尚未访问的相邻结点,执行回溯,回到结点 2;
- <9> 第九步,按照 2 => 5 => 4 => 1 => 0 的顺序一路回溯,搜索结束;
- 如 图三-2 所示,红色实箭头表示搜索路径,蓝色虚箭头表示回溯路径。
- 所以上图的遍历序列为:
0 -> 1 -> 3 -> 4 -> 5 -> 2 -> 6
2)算法实现
const int MAXN = 7;
void dfs(int u) {
if(visit[u]) {
// 1
return ;
}
visit[u] = true; // 2
dfs_add(u); // 3
for(int i = 0; i < MAXN; ++i) {
int v = i;
if(adj[u][v]) {
// 4
dfs(v); // 5
}
}
}
- 1、
visit[MAXN]数组是一个bool数组,用于标记某个节点是否已访问,初始化都为 false;这里对已访问结点执行回溯; - 2、
visit[u] = true;对未访问结点 u 标记为已访问状态; - 3、
dfs_add(u);用来将 u 存储到的访问序列中,实际函数实现如下:
void dfs_add(int u) {
ans[ansSize++] = u;
}
- 4、
adj[MAXN][MAXN]是图的邻接矩阵,用 0 或 1 来代表点是否连通,对于上面的例子,邻接矩阵表示如下:
bool adj[MAXN][MAXN] = {
{
0, 1, 1, 0, 0, 0, 0},
{
1, 0, 0, 1, 1, 0, 0},
{
1, 0, 0, 0, 0, 1, 1},
{
0, 1, 0, 0, 0, 0, 0},
{
0, 1, 0, 0, 0, 1, 0},
{
0, 0, 1, 0, 1, 0, 0},
{
0, 0, 1, 0, 0, 0, 0},
};
(adj[u][v] = 1代表 u 和 v 之间有一条有向边;adj[u][v] = 0代表没有边)
- 5、递归调用相邻结点;
3)基础应用
a. 求阶乘
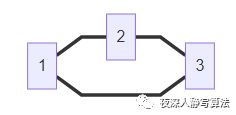
【例题2】给出 n ( n < = 10 ) n ( n <= 10 ) n(n<=10),求 n ! = n ∗ ( n − 1 ) ∗ . . . ∗ 3 ∗ 2 ∗ 1 n! = n*(n-1)*...*3*2*1 n!=n∗(n−1)∗...∗3∗2∗1;
- 令 f ( n ) = n ! f(n) = n! f(n)=n!,那么有 f ( n ) = n ∗ f ( n − 1 ) f(n) = n * f(n-1) f(n)=n∗f(n−1) ( n > 0 ) (n>0) (n>0)。由于满足递归的性质,可以认为这是一个 n + 1 n+1 n+1 个结点的图,结点 i ( i > = 1 ) i (i >= 1) i(i>=1) 到结点 i − 1 i-1 i−1 有一条权值为 i i i 的有向边,从 n n n 开始进行深度优先搜索,搜索的终点是结点 0 0 0,返回值为 1 (即 0 ! = 1 0! = 1 0!=1)。

- 如 图三-3 所示, n ! n! n! 的递归计算看成是一个深度优先搜索的过程,并且每次回溯的时候会将遍历的结果返回给上一个结点(当然,这只是一个思想,并不代表这是求 n ! n! n! 的高效算法)。
- C++ 代码实现如下:
int dfs(int n) {
return !n ? 1 : n * dfs(n-1);
}
(由于 C++ 中的 int 是 32 位整数,最大能够表示的值为 2 31 − 1 2^{31}-1 231−1,所以这里的 n 太大就会导致溢出,需要用数组来模拟实现高精度,这个也会在后面的章节来详细讲解如何实现一个高精度的四则运算)
b. 求斐波那契数列的第n项
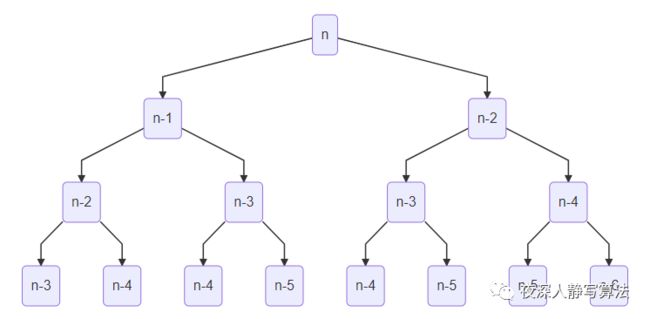
【例题3】令 g ( n ) = g ( n − 1 ) + g ( n − 2 ) g(n) = g(n-1) + g(n-2) g(n)=g(n−1)+g(n−2), ( 1 < n < 40 ) (1 < n < 40) (1<n<40),其中 g ( 0 ) = g ( 1 ) = 1 g(0) = g(1) = 1 g(0)=g(1)=1;
- 同样可以利用图论的思想,从结点 n n n 向 n − 1 n-1 n−1 和 n − 2 n-2 n−2 分别引一条权值为1的有向边,每次求 g ( n ) g(n) g(n) 就是以 n n n 作为起点,对 n n n 进行深度优先搜索,然后将 n − 1 n -1 n−1 和 n − 2 n-2 n−2 回溯的结果相加作为 n n n 结点的值,即 g ( n ) g(n) g(n)。
- C++ 代码实现如下:
int dfs(unsigned int n) {
if(n <= 1) {
return 1;
}
return dfs(n-1) + dfs(n-2);
}
- 这里会带来一个问题, g ( n ) g(n) g(n) 的计算需要用到 g ( n − 1 ) g(n-1) g(n−1) 和 g ( n − 2 ) g(n-2) g(n−2) ,而 g ( n − 1 ) g(n-1) g(n−1) 的计算需要用到 g ( n − 2 ) g(n-2) g(n−2) 和 g ( n − 3 ) g(n-3) g(n−3),所以我们发现 g ( n − 2 ) g(n-2) g(n−2) 被用到了两次,而且每个结点都存在这个问题,这样就使得整个算法的时间复杂度变成指数级了,对于斐波那契数列递归算法的时间复杂度分析,可以参考这篇文章:斐波那契数列递归时间复杂度分析
- 为了规避这个问题,下面会讲到基于深搜的记忆化搜索。
c. 求 n 个数的全排列
【例题4】给定 n n n, 按字典序输出 1 到 n n n 的所有全排列;
- 全排列的种数是 n ! n! n!,要求按照字典序输出。这是最典型的深搜问题。我们可以把 n n n 个数两两建立无向边(即任意两个结点之间都有边,也就是一个 n n n 个结点的完全图),然后对每个点作为起点,分别做一次深度优先搜索,当所有点都已经标记时,输出当前的搜索路径,就是其中一个排列;
- 这里需要注意的是,回溯的时候需要将原先标记的点的标记取消,否则只能输出一个排列。如果要按照字典序,则需要在遍历的时候保证每次遍历都是按照结点从小到大的方式进行遍历的。
- C++ 代码实现如下:
void dfs(int depth) {
// 1
if(depth == MAXN) {
// 2
dfs_print();
return;
}
for(int i = 1; i <= MAXN; ++i) {
int v = i;
if(!visit[v]) {
// 3
dfs_add(v); // 4
dfs(depth+1);
dfs_dec(v);
}
}
}
- 1)这里的
depth参数用来做计数用,表明本次遍历了多少个结点; - 2)当遍历元素达到
MAXN个的时候,输出访问的元素列表; - 3)
visit[v]用来判断 v v v 这个元素是否有访问过; - 4)
dfs_add和dfs_dec分别表示将结点从访问列表加入和删除;
void dfs_add(int u) {
visit[u] = true;
ans[ansSize] = u;
++ansSize;
}
void dfs_dec(int u) {
--ansSize;
visit[u] = false;
}
4)高级应用
a. 枚举
- 数据范围较小的的排列、组合的穷举。
b. 容斥原理
- 主要用于组合数学中的计数统计,会在后面的章节详细介绍。
c. 基于状态压缩的动态规划
- 一般解决棋盘摆放问题, k k k 进制表示状态,然后利用深搜进行状态转移,会在后面的章节详细介绍。
d.记忆化搜索
- 某个状态已经被计算出来,就将它 cache 住,利用数组或者哈希表将它的值存储下来,下次要用的时候不需要重新求,此所谓记忆化。本章节会详细讲到记忆化搜索的应用范围。
e.有向图强连通分量
- 经典的 T a r j a n Tarjan Tarjan 算法,求解 2 − s a t 2-sat 2−sat 问题的基础,会在后面的章节详细介绍。
f. 无向图割边割点和双连通分量
- 经典的 T a r j a n Tarjan Tarjan 算法,会在后面的章节详细介绍。
g. LCA 最近公共祖先
- 最近公共祖先递归求解,会在后面的章节详细介绍。
h.博弈
- 利用深搜计算SG值,会在后面的章节详细介绍。
i.二分图最大匹配
- 经典的匈牙利算法,最小顶点覆盖、最大独立集、最小值支配集 向二分图的转化,会在后面的章节详细介绍。
j.欧拉回路
- 经典的圈套圈算法,会在后面的章节详细介绍。
k.K短路
- 依赖数据,数据不卡的话可以采用2分答案 + 深搜;也可以用广搜 + A*。
l. 线段树
- 二分经典思想,配合深搜枚举左右子树,求和、最值等问题,会在后面的章节详细介绍。
m. 最大团
- 极大完全子图的优化算法,会在后面的章节详细介绍。
n. 最大流
- EK算法求任意路径中有涉及,会在后面的章节详细介绍。
o. 树形DP
- 即树形动态规划,父结点的值由各个子结点计算得出,会在后面的章节详细介绍。
2、基于DFS的记忆化搜索
1)算法原理
- 上文中已经提到记忆化搜索,其实就是类似动态规划的思想,每次将已经计算出来的状态的值存储到数组或者哈希表中,下次需要的时候直接记录的值,避免重复计算。
【例题5】如图三-7所示,图中的橙色小方块就是传说中的作者,他可以在一个 n*m 的棋盘上行走,但是只有两个方向,一个是向右,一个是向下(如绿色箭头所示),棋盘上有很多的金矿,走到格子上就能取走那里的金矿,每个格子的金矿数目不同(用蓝色数字表示金矿的数量),问作者在这样一个棋盘上最多可以拿到多少金矿。
图三-7
- 我们用函数 D F S ( i , j ) DFS(i, j) DFS(i,j) 表示从 ( 1 , 1 ) (1, 1) (1,1) 到 ( i , j ) (i, j) (i,j) 可以取得金矿的最大值,那么要到达 ( i , j ) (i, j) (i,j) 这个点,要么是从 ( i , j − 1 ) (i, j-1) (i,j−1) 过来,要么是从 ( i − 1 , j ) (i-1, j) (i−1,j) 过来,所以就有如下方程:
D F S ( i , j ) = g o l d [ i ] [ j ] + m a x { D F S ( i , j − 1 ) , D F S ( i − 1 , j ) } DFS(i, j) = gold[i][j] + max\{ DFS(i, j-1), DFS(i-1, j) \} DFS(i,j)=gold[i][j]+max{ DFS(i,j−1),DFS(i−1,j)} - 满足递归性质就可以进行深度优先搜索了,于是遇到了和求斐波那契数列一样的问题, D F S ( i , j ) DFS(i, j) DFS(i,j) 可能会被计算两次,每个结点都被计算两次的话复杂度就是指数级了。
- 所以这里我们可以利用一个二维数组,令 D [ i ] [ j ] = D F S ( i , j ) D[i][j] = DFS(i, j) D[i][j]=DFS(i,j),初始化所有的 D [ i ] [ j ] = − 1 D[i][j] = -1 D[i][j]=−1,表示尚未计算,每次搜索到 ( i , j ) (i, j) (i,j) 这个点时,检查 D [ i ] [ j ] D[i][j] D[i][j] 的值,如果为 -1,则进行计算,将计算结果赋值给 D [ i ] [ j ] D[i][j] D[i][j] ;否则直接返回 D [ i ] [ j ] D[i][j] D[i][j] 的值。
- 记忆化搜索虽然叫搜索,实际上还是一个动态规划问题,能够记忆化搜索的一般都能用动态规划求解,但是记忆化搜索的编码更加直观、易写。
2)算法实现
- C++ 代码实现如下:
int dfs(int i, int j) {
if(i == 0 && j == 0) {
// 1
return D[0][0] = gold[0][0];
}
if(i < 0 || j < 0) {
// 2
return 0;
}
if(D[i][j] != -1) {
// 3
return D[i][j];
}
return D[i][j] = gold[i][j] + max(dfs(i-1,j), dfs(i, j-1)); // 4
}
-
1)当 i i i 和 j j j 都为 0,代表起点,直接返回起点的金矿值;
-
2)当 i < 0 i < 0 i<0 或者 j < 0 j < 0 j<0 时, 代表是个不合法的点,则直接返回最小值 0;
-
3)当 D [ i ] [ j ] D[i][j] D[i][j] 不等于默认值 -1 时,说明之前已经通过其他途径遍历到 ( i , j ) (i,j) (i,j) 这个点并且已经计算过最优值,可以直接返回。
-
4)利用递归计算 ( i , j ) (i,j) (i,j) 这个点的最优值,并且赋值给 D [ i ] [ j ] D[i][j] D[i][j] 作为记忆化。
-
样例的计算结果如下:
0 0 0 1 1 1
0 0 2 2 7 7
0 3 3 8 8 8
1 3 5 8 8 8
- 关于记忆化搜索的内容,本文只作简要入门级介绍,如果不理解,问题也不大,我将会在后面的章节继续展开加强理解。
3、基于DFS的剪枝
1)算法原理
- 搜索的过程可以看作是从树根出发,遍历一棵倒置的树——搜索树的过程。而剪枝,顾名思义,就是通过某种判断,避免一些不必要的遍历过程,形象的说,就是剪去了搜索树中的某些“枝条”,故称剪枝(原话取自1999年OI国家集训队论文《搜索方法中的剪枝优化》(齐鑫))。
- 如图三-8所示,它是一棵利用深度优先搜索遍历的搜索树,可行解(或最优解)位于黄色的叶子结点,那么根结点的最左边的子树完全没有必要搜索(因为不可能出解)。如果我们在搜索的过程中能够清楚地知道哪些子树不可能出解,就没必要往下搜索了,也就是将连接不可能出解的子树的那根“枝条”剪掉,图中红色的叉对应的“枝条”都是可以剪掉的。
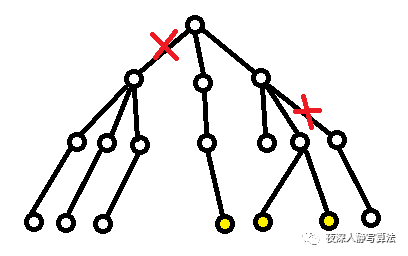
- 好的剪枝可以大大提升程序的运行效率,那么问题来了,如何进行剪枝?我们先来看剪枝需要满足什么原则:
a. 正确性
- 剪掉的子树中如果存在可行解(或最优解),那么在其它的子树中很可能搜不到解导致搜索失败,所以剪枝的前提必须是要正确;
b. 准确性
- 剪枝要“准”。所谓“准”,就是要在保证在正确的前提下,尽可能多得剪枝。
c. 高效性
- 剪枝一般是通过一个函数来判断当前搜索空间是否是一个合法空间,在每个结点都会调用到这个函数,所以这个函数的效率很重要。
- 剪枝大致可以分成两类:可行性剪枝、最优性剪枝(上下界剪枝)。
2)可行性剪枝
- 可行性剪枝一般是处理可行解的问题,如一个迷宫,问能否从起点到达目标点之类的。
【例题6】如图三-9所示,问作者能否在正好第 11 秒的时候避过各种障碍物(图中的东西一看就知道哪些是障碍物了,_)最终取得爱心,作者每秒能且只能移动一格,允许走重复的格子。
图三-9
- 仔细分析可以发现,这是永远不可能的,因为作者无论怎么走,都只能在第偶数秒的时候到达爱心的位置,这是他们的曼哈顿距离(两点的XY坐标差的绝对值之和)的奇偶性决定的,所以这里我们可以在搜索的时候做奇偶性剪枝(可行性剪枝)。
- 类似的求可行解的问题还有很多,如 N ( N < = 25 ) N (N <= 25) N(N<=25) 根长度不一的木棒,问能否选取其中几根,拼出长度为 K K K 的木棒,具体就是枚举取木棒的过程,每根木棒都有取或不取两种状态,所以总的状态数为 2 25 2^{25} 225,需要进行剪枝。用到的是剩余和不可达剪枝(随便取的名字,即当前 S S S 根木棒取了 S 1 S_1 S1 根后,剩下的 N − S N-S N−S 根木棒的总和 加上 之前取的 S 1 S_1 S1 根木棒总和如果小于 K K K,那么必然不满足,没必要继续往下搜索了),这个问题其实是个01背包,当 N N N 比较大的时候就是动态规划了。
3)最优性剪枝(上下界剪枝)
- 最优性剪枝一般是处理最优解的问题。以求两个状态之间的最小步数为例,搜索最小步数的过程:一般情况下,需要保存一个“当前最小步数”,这个最小步数就是当前解的一个下界d。在遍历到搜索树的叶子结点时,得到了一个新解,与保存的下界作比较,如果新解的步数更小,则令它成为新的下界。搜索结束后,所保存的解就是最小步数。而当我们已经搜索了k歩,如果能够通过某种方式估算出当前状态到目标状态的理论最少步数 s 时,就可以计算出起点到目标点的理论最小步数,即估价函数 h = k + s,那么当前情况下存在最优解的必要条件是h < d,否则就可以剪枝了。最优性剪枝是不断优化解空间的过程。
- 关于剪枝技巧还有很多,本文就不多展开了,后面章节会专门对剪枝技巧进行一个梳理,详细剖析每个问题。
4、基于DFS的A*(迭代加深,IDA*)
1)算法原理
- 迭代加深就是深度优先搜索加上 A* 估价函数进行剪枝,应用相对较为局限,但是对于处理某些问题有奇效,本文会举一个比较简单的例子,后面章节会详细展开来讲以加深理解。
迭代加深算法原理如下:
1、枚举深度。
2、根据限定的深度进行 dfs,并且利用估价函数进行剪枝。
- 算法原理本身很简单,难点在于估价函数的选取和实现。
2)算法实现
void IDA_Star(int startState) {
int maxDepth = 0;
while (true) {
if(dfs(startState, 0, maxDepth)) {
return ;
}
maxDepth = maxDepth + 1;
}
}
3)简单举例
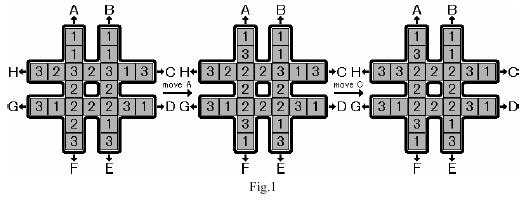
【例题7】如图三-10所示,一个“井”字形的玩具,上面有三种数字1、2、3,给出8种操作方式,A表示将第一个竖着的列循环上移一格,并且A和F是一个逆操作,B、C、D…的操作方式依此类推,初始状态给定,目标状态是中间8个数字相同。问最少的操作方式,并且要求给出操作的序列,步数一样的时候选择字典序最小的输出。图中的操作序列为AC。
图三-10
- 大致分析一下,一共24个格子,每个格子三种情况,所以最坏情况状态总数为 3 24 3^{24} 324,但实际上,我们可以分三种情况讨论,先确定中间的8个数字的值,假设为1的话,2和3就可以看成是一样的,于是状态数变成了 2 24 2^{24} 224。
- 对三种情况分别进行迭代加深搜索,令当前需要搜索的中间8个数字为k,首先枚举本次搜索的最大深度 maxDepth(即需要的步数),从初始状态进行状态扩展,每次扩展 8 个结点,当搜索到深度为depth的时候,那么剩下可以移动的步数为 maxDepth - depth,我们发现每次移动,中间的 8 个格子最多多一个 k,所以如果当前状态下中间 8 个格子有 sum 个 k,那么需要的剩余步数的理想最小值 s = 8 - sum,那么估价函数:
h = d e p t h + ( 8 − s u m ) h = depth + (8 - sum) h=depth+(8−sum) - 当 h > m a x D e p t h h > maxDepth h>maxDepth 时,表明在当前这种状态下,不可能在 maxDepth 歩以内达成目标,直接回溯。
- 当某个深度maxDepth至少有一个可行解时,整个算法也就结束了,可以设定一个标记,直接回溯到最上层,或者在DFS的返回值给定,对于某个搜索树,只要该子树下有解就返回 1,否则返回 0。
- 迭代加深适合深度不是很深,但是每次扩展的结点数很多的搜索问题。
四、广度优先搜索
1、BFS
1)算法原理
- 广度优先搜索即Breadth First Search,也是图遍历算法的一种。用一句话概括就是:“我会分身我怕谁?!”。BFS的具体算法描述为:
选择一个起始点 u 放入一个先进先出的队列中,执行如下操作:
a. 如果队列不为空,弹出一个队列首元素,记为 当前结点,执行b;否则算法结束;
b. 将与 当前结点 相邻并且尚未被访问的结点的信息进行更新,并且全部放入队列中,继续执行a;
- 维护广搜的数据结构是队列和哈希表,也就是很多数据结构书上所说的 o p e n − c l o s e open-close open−close 表,哈希表主要是用来标记状态的,比如某个状态并不是一个整数,可能是一个字符串,就需要用字符串映射到一个整数,可以自己写个散列哈希表,不建议用STL的map,效率奇低。
- 广搜最基础的应用是用来求图的最短路。
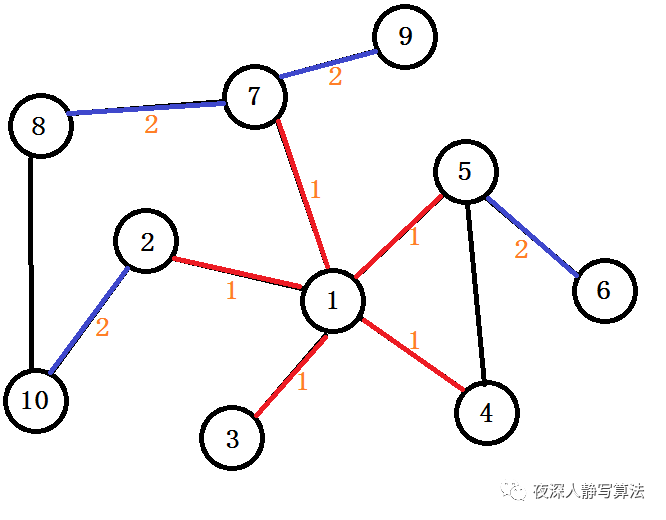
【例题8】给定一个无向连通图,如果两个结点间有直接的边那么权值就是1,求从1号结点出发,到所有点的最短距离。
图四-1
- 如图四-1所示,对以下图进行广度优先搜索;
- 1)起点为1,将它放入队列后。那么第一次从队列中弹出的一定是1,将和1相邻未被访问的结点继续按顺序放入队列中,分别是2、3、4、5、7,并且记录下它们距离起点的距离dis[x] = dis[1] + 1 (x 属于集合 {2, 3, 4, 5, 7});
- 2)然后弹出的元素是2,和2相邻未被访问的结点是10,将它也放入队列中,记录dis[10] = dis[2] + 1;
- 3)接着弹出5,放入6(4由于已经被访问过,所以不需要再放入队列中);
- 4)弹出7,放入8、9。队列为空后结束搜索,搜索完毕后,dis 数组就记录了起点1到各个点的最短距离;
2)算法实现
const int inf = -1;
void bfs(int u) {
queue <int> q;
memset(dis, inf, sizeof(dis)); // 1
dis[u] = 0;
q.push(u);
while(!q.empty()) {
u = q.front(); // 2
q.pop();
for(int v = 1; v <= n; ++v) {
if(!adj[u][v]) continue; // 3
if(dis[v] != inf) continue; // 4
dis[v] = dis[u] + 1; // 5
q.push(v);
}
}
}
- 1)
dis[u]数组用来标记从起点到 u 的最短距离,初始化为 -1 代表无限远; - 2)每次从队列中弹出一个元素,这里队列采用 STL 的动态队列;
- 3)
adj[u][v]=0代表不连通,则直接跳过; - 4)
dis[v] != inf代表 v 这个结点已经访问过,则直接跳过; - 5)扩展下一个结点,并且放入队列中,等待下次弹出;
3)基础应用
a. 最短路
- bellman-ford最短路的优化算法SPFA,主体是利用BFS实现的,会在后面的章节详细介绍。
- 绝大部分四向、八向迷宫的最短路问题。
b. 拓扑排序
- 首先找入度为0的点入队,弹出元素执行“减度”操作,继续将减完度后入度为0的点入队,循环操作,直到队列为空,经典BFS操作,会在后面的章节详细介绍。
c. FloodFill
- 经典洪水灌溉算法。
4)高级应用
a. 差分约束
- 数形结合的经典算法,利用SPFA来求解不等式组,会在后面的章节详细介绍。
b. 稳定婚姻
- 二分图的稳定匹配问题,试问没有稳定的婚姻,如何有心思学习算法,所以一定要学好BFS啊。
c. AC自动机
- 字典树 + KMP + BFS,在设定失败指针的时候需要用到BFS。
- 详细算法参见:http://www.cppblog.com/menjitianya/archive/2014/07/10/207604.html
d. 矩阵二分
- 矩阵乘法的状态转移图的构建可以采用BFS,会在后面的章节详细介绍。
e. 基于k进制的状态压缩搜索
- 这里的k一般为2的幂,状态压缩就是将原本多维的状态压缩到一个k进制的整数中,便于存储在一个一维数组中,往往可以大大地节省空间,又由于k为2的幂,所以状态转移可以采用位运算进行加速,HDU1813 和 HDU3278 以及 HDU3900 都是很好的例子。
f. 基于A*的广度优先搜索
- 在搜索的时候,结点信息要用堆(优先队列)维护大小,即能更快到达目标的结点优先弹出。
- 对于 A*算法,会在后面的章节详细介绍。
g.双向广搜
- 适用于 起始状态 和 结束状态 都已知的情况,能够将状态空间进行开根号。
- 关于双向广搜的内容,会在后面的章节详细介绍。
本文所有示例代码均可在以下 github 上找到:github.com/WhereIsHeroFrom/模板/图论
![]()
五、搜索题集整理
1、DFS题集
| 题目链接 | 难度 | 解法 |
|---|---|---|
| Red and Black | ★☆☆☆☆ | FloodFill |
| The Game | ★☆☆☆☆ | FloodFill |
| Frogger | ★☆☆☆☆ | 二分枚举答案 + FloodFill |
| Nearest Common Ancestors | ★☆☆☆☆ | 最近公共祖先 |
| Robot Motion | ★☆☆☆☆ | 递归模拟 |
| Dessert | ★☆☆☆☆ | 枚举 |
| Matrix | ★☆☆☆☆ | 枚举 |
| Frame Stacking | ★☆☆☆☆ | 枚举 |
| Transportation | ★☆☆☆☆ | 枚举 |
| Pairs of Integers | ★★☆☆☆ | 枚举 |
| 方程的解数 | ★★☆☆☆ | 枚举 + 散列HASH |
| Maze | ★★☆☆☆ | 建完图后FloodFill |
| Trees Made to Order | ★★☆☆☆ | 递归构造解 |
| Cycles of Lanes | ★★☆☆☆ | 简单图最长环 |
| The Settlers of Catan | ★★☆☆☆ | 简单图最长链 |
| Parity game | ★★☆☆☆ | 简单图判奇环(交错染色) |
| Increasing Sequences | ★★☆☆☆ | 枚举 |
| Necklace Decomposition | ★★☆☆☆ | 枚举 |
| Rikka with Tree | ★★☆☆☆ | 统计 |
| Mahjong tree | ★★★☆☆ | 统计 |
| Machine Schedule | ★★★☆☆ | 二分图最大匹配 |
| Chessboard | ★★★☆☆ | 棋盘覆盖问题 |
| Air Raid | ★★★☆☆ | DAG图 最小路径覆盖 |
| Entropy | ★★★☆☆ | 枚举 + 适当剪枝 |
| Dropping the stones | ★★★☆☆ | 枚举 + 适当剪枝 |
| Dreisam Equations | ★★★☆☆ | 表达式求值 |
| Firefighters | ★★★☆☆ | 表达式求值 |
| Cartesian Tree | ★★★☆☆ | 笛卡尔树的构造 |
| Binary Stirling Numbers | ★★★☆☆ | 分形 |
| Obfuscation | ★★★☆☆ | 字符串匹配 |
| Graph Coloring | ★★★☆☆ | 最大团 |
| Pusher | ★★★☆☆ | 暴力搜索 |
| Self-Replicating Numbers | ★★★★☆ | 枚举 |
| Last Digits | ★★★★☆ | DFS + 欧拉函数 |
| Secret Code | ★★★★☆ | 实复数进制转化 |
| Anniversary Cake | ★★★★☆ | 矩形填充 |
| A Puzzling Problem | ★★★★☆ | 枚举摆放 |
| Vase collection | ★★★★☆ | 图的完美匹配 |
| Packing Rectangles | ★★★★☆ | 枚举摆放 |
| Missing Piece 2001 | ★★★★☆ | N*N-1 数码问题,强剪枝 |
2、IDA*题集
| 题目链接 | 难度 | 解法 |
|---|---|---|
| Addition Chains | ★★☆☆☆ | |
| DNA sequence | ★★☆☆☆ | |
| Booksort | ★★★☆☆ | |
| The Rotation Game | ★★★☆☆ | 迭代加深的公认经典题,理解“最少剩余步数” |
| Paint on a Wall | ★★★☆☆ | The Rotation Game 的简单变形 |
| Escape from Tetris | ★★★★☆ | |
| Maze | ★★★★☆ | |
| Rubik 2×2×2 | ★★★★★ | 编码麻烦的魔方题 |
3、BFS 题集
| 题目链接 | 难度 | 解法 |
|---|---|---|
| Pushing Boxes | ★☆☆☆☆ | 经典广搜 - 推箱子 |
| Jugs | ★☆☆☆☆ | 经典广搜 - 倒水问题 |
| Space Station Shielding | ★☆☆☆☆ | FloodFill |
| Knight Moves | ★☆☆☆☆ | 棋盘搜索 |
| Knight Moves | ★☆☆☆☆ | 棋盘搜索 |
| Eight | ★★☆☆☆ | 经典八数码 |
| Currency Exchange | ★★☆☆☆ | SPFA |
| The Postal Worker Rings | ★★☆☆☆ | SPFA |
| ROADS | ★★☆☆☆ | 优先队列应用 |
| Ones | ★★☆☆☆ | 同余搜索 |
| Dogs | ★★☆☆☆ | |
| Lode Runner | ★★☆☆☆ | |
| Hike on a Graph | ★★☆☆☆ | |
| Find The Multiple | ★★☆☆☆ | 同余搜索 |
| Different Digits | ★★★☆☆ | 同余搜索 |
| Magic Multiplying Machine | ★★★☆☆ | 同余搜索 |
| Remainder | ★★★☆☆ | 同余搜索 |
| Escape from Enemy Territory | ★★★☆☆ | 二分答案 + BFS |
| Will Indiana Jones Get | ★★★☆☆ | 二分答案 + BFS |
| Fast Food | ★★★☆☆ | SPFA |
| Invitation Cards | ★★★☆☆ | SPFA |
| Galactic Import | ★★★☆☆ | SPFA |
| XYZZY | ★★★☆☆ | 最长路判环 |
| Intervals | ★★★☆☆ | 差分约束 |
| King | ★★★☆☆ | 差分约束 |
| Integer Intervals | ★★★☆☆ | 差分约束 |
| Sightseeing trip | ★★★☆☆ | 无向图最小环 |
| N-Credible Mazes | ★★★☆☆ | 多维空间搜索,散列HASH |
| Spreadsheet | ★★★☆☆ | 建立拓扑图后广搜 |
| Frogger | ★★★☆☆ | 同余搜索 |
| Ministry | ★★★☆☆ | 需要存路径 |
| Gap | ★★★☆☆ | A* |
| Maze | ★★★☆☆ | 二进制压缩钥匙的状态 |
| Hike on a Graph | ★★★☆☆ | |
| All Discs Considered | ★★★☆☆ | |
| Roads Scholar | ★★★☆☆ | SPFA |
| Holedox Moving | ★★★☆☆ | |
| 昂贵的聘礼 | ★★★☆☆ | |
| Maze Stretching | ★★★☆☆ | |
| Treasure of the Chimp | ★★★☆☆ | |
| Is the Information Reliable | ★★★☆☆ | 最长路判环 |
| It’s not a Bug, It’s a | ★★★☆☆ | |
| Warcraft | ★★★☆☆ | |
| Escape | ★★★☆☆ | |
| Bloxorz I | ★★★☆☆ | 当年比较流行这个游戏 |
| Up and Down | ★★★★☆ | 离散化 + BFS |
| Sightseeing | ★★★★☆ | SPFA |
| Cliff Climbing | ★★★★☆ | 日本人的题就是这么长 |
| Cheesy Chess | ★★★★☆ | 仔细看题 |
| The Treasure | ★★★★☆ | |
| Chessman | ★★★★★ | 弄清状态同余的概念 |
| Puzzle | ★★★★★ | 几乎尝试了所有的搜索 -_- |
| Unblock Me | ★★★★★ | 8进制压缩状态,散列HASH,位运算加速 |
4、双向BFS 题集
| 题目链接 | 难度 | 解法 |
|---|---|---|
| Solitaire | ★★★☆☆ | |
| A Game on the Chessboard | ★★★☆☆ | |
| 魔板 | ★★★★☆ | |
| Tobo or not Tobo | ★★★★☆ | |
| Eight II | ★★★★★ |