夜深人静写算法（十）- 单向广搜

一、前言

  掌握了广搜就意味着至少可以拿一块省赛银牌，这或许是一句玩笑话，但是我觉得还是有几分道理的，广搜的涉及面很广，而且可以辅助你更好得理解动态规划，因为两者都有状态的概念，而且广搜的状态更加容易构造，不学广搜就无法理解 A*、SPFA、差分约束、稳定婚姻、最大流 等等其它的图论算法。
  回想自己十几年前刚开始学习搜索的时候，总是分不清楚什么时候应该用广搜，什么时候应该用深搜，所以，我把之前遇到的问题做了一个总结，发现最重要的还是那两个字：状态。今天这篇文章会围绕这两个字进行一个非常详细的讲解。
  当然，任何事情都有一个循序渐进的过程，我不会把所有关于广搜的内容一次性讲完，看完这篇文章，你至少应该可以自己手写一个单向广搜的代码。后面的章节会对 最短路、A* 、双向广搜 逐一进行讲解。

二、单向广搜简介

• 单向广搜就是最简化情况下的广度优先搜索（Breadth First Search），以下简称为广搜。游戏开发过程中用到的比较广泛的 A* 寻路，就是广搜的加强版。
• 那么，我们通过一个例子来初步了解下广搜的搜索过程。

【例题1】公主被关在一个 $n\times m(n,m<=500)$ 的迷宫里，主公想在最快的时间内救出公主。但是迷宫太大，而且有各种墙阻挡，主公每次只能在 上、下、左、右 四个方向内选择周围的非墙体格子前进一格，并且花费 1 单位时间，问主公救出公主的最少时间。

图二-1 （图中 ♂ 代表主公，♀代表公主，□ 代表墙体不能通行）

• 这个问题就是经典的用广度优先搜索来解决的问题。
• 我们通过一个动图来对广搜有一个初步的印象，如图二-2所示：
  图二-2
• 从图中可以看出，广搜的本质还是暴力枚举。即对于每个当前位置，枚举四个相邻可以行走的方向进行不断尝试，直到找到目的地。有点像洪水爆发，从一个源头开始逐渐蔓延开来，直到所有可达的区域都被洪水灌溉，所以我们也把这种算法称为 FloodFill。
• 那么，如何把它描述成程序的语言呢？这里需要用到一种数据结构 —— 队列。本文接下来会对这种数据结构进行一个详细的讲解，如果读者对队列已经耳熟能详，那么可以跳过第三节，直接进入第四节。

三、先进先出队列

• 常见的队列有：先进先出队列、优先队列、单调队列 等等。本章将主要介绍 先进先出队列。
• 数据结构中的先进先出队列就好比我们日常工作中去食堂排队吃饭，排在前面的先取到饭。而 “先进先出” 就是 “先到先得” ，“近水楼台先得月” 的意思。读者可以从任何一本数据结构的书籍上看到这么一个词汇 FIFO，它就是先进先出（First Input First Output）的简称。
• 为了方便读者阅读，接下来一律将 先进先出队列 简称为 队列。

1、队列的基础结构

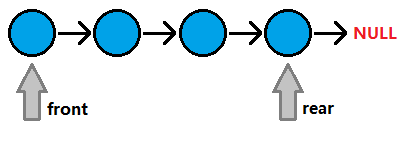
• 队列的基础结构是一种线性表，所以实现方式主要有两种：链表 和 数组。并且需要两个指针，分别指向队列头 $front$ 和队列尾 $rear$。

• 链表结构的队列如下：
  

  图三-1-1

• 数组结构的队列如下：
  

  图三-1-2

• 那么接下来，请忘记链表。

• 作者将介绍一种用数组的方式来实现的队列，结构定义如下：

class Queue {
     
public:
    Queue();
    virtual ~Queue();
public:
    ...
private:
    QueueData *data_;
    int front_, rear_;
};

• 1）QueueData *data_：虽然是个指针，但是它不是链表，这个指针指向的是队列数据的内存首地址，由于队列数组较大，所以采用堆内存，在队列类的构造函数里进行内存申请，析构函数里进行内存释放，代码如下：

const int MAXQUEUE = 1000000;

Queue::Queue() : data_(NULL) {
     
    data_ = new QueueData[MAXQUEUE];
}

Queue::~Queue() {
     
    if (data_) {
     
        delete[] data_;
        data_ = NULL;
    }
}

• 2）front_代表了队列头数据的索引，是一个数组下标，所以是整数类型，当队列不为空的时候，data_[front_]获取到的就是队首元素；
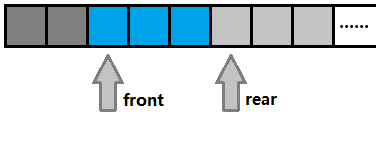
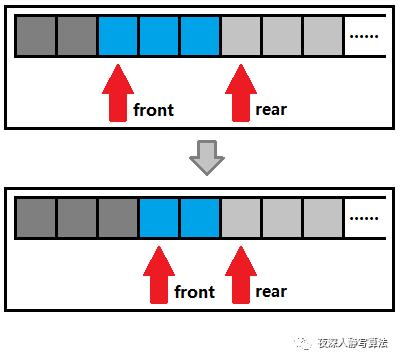
• 3）rear_代表了队列尾，也是一个数组下标，和队列首不同，它指向的是一个无用位置（空结点），当队列不为空的时候，队列尾部最后一个可用数据为data_[rear_-1]，如图三-1-3所示：

图三-1-3

• 图中深灰色代表已经弹出的数据，蓝色代表队列内的数据，浅灰色代表尚未使用的数据；

2、队列的数据元素

• 队列的数据元素一般是一个结构体（或者类），即上文提到的QueueData，这样就可以根据不同需求定义不同的数据类型。
• 这个结构体的成员变量可以只有一个整数，代表 身高、年龄；

struct QueueData {
     
    int height;
};

struct QueueData {
     
    int age;
};

• 也可以是两个整数，代表 二维空间的坐标位置、一个矩形的宽和高 等等；

struct QueueData {
     
    int x, y;
};

struct QueueData {
     
    int width, height;
};

• 也可以是三个整数，代表 三维空间的位置、亦或是二维空间的位置加上方向等等。

struct QueueData {
     
    int x, y, z;
};

struct QueueData {
     
    int x, y, dir;
};

3、队列的接口

• 队列的操作接口一共有三种：清空队列、压入数据、弹出数据；
• 队列的判定接口只有一个：判空；

class Queue {
     
    ...
public:
    void clear();                    // 1）清空队列
    void push(const QueueData& bs);  // 2）压入数据
    QueueData& pop();                // 3）弹出数据
public:
    bool empty() const;              // 4）队列是否为空
private:
    ...
};

1）清空队列

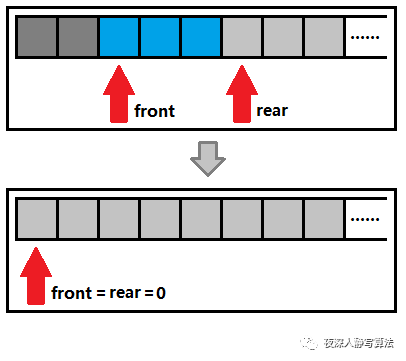
• 清空队列不实际进行内存释放，而只是将队列头和队列尾下标索引置零，如下：

void Queue::clear() {
     
    front_ = rear_ = 0;
}

图三-3-1

2）压入数据

• 压入数据的过程是将传入的数据结构体拷贝到队列尾指向的内存上，然后再将队列尾指针下标自增 1，时间复杂度 $O(1)$。

void Queue::push(const QueueData& bs) {
     
    data_[rear_++] = bs;
}

图三-3-2

3）弹出数据

• 弹出数据的过程是将队列头的数据的结构体引用直接返回给调用方，然后队列头指针下标自增 1，时间复杂度 $O(1)$。

QueueData& Queue::pop(){
     
    return data_[front_++];
}

图三-3-3

4）队列判空

• 队列的判定接口只有一个：判空；
• 只需要判断 队列头索引 和 队列尾索引 是否相同即可；

bool Queue::empty() const {
     
    return front_ == rear_;
}

4、队列的容错机制

• 上文在实现队列的时候，为了尽量简化代码，做了一些偷懒，所以是存在问题的，主要有两个：
• 1）队列为空的时候，进行弹出数据操作，得到的是一个未知的元素，是上一次残留的缓存数据，所以调用方在使用队列接口的时候需要进行先判空，再弹出的操作；
• 2）当队列数据超出了给定最大元素MAXQUEUE时，压入数据会导致数组下标越界，有两个解决方案：
• • a. 循环队列；
• • b. 动态扩容；

1）循环队列

• 我们发现，当弹出数据后，data_[0, front_ - 1]这块内存的数据再也没有被用到，所以是可以被重复利用的，具体做法是：
• a）当压入数据后，使得队列尾指针等于MAXQUEUE时，则队列尾指针置0；修改后的 push接口，代码实现如下：

void Queue::push(const QueueData& bs) {
     
    data_[rear_++] = bs;
    if (rear_ == MAXQUEUE) rear_ = 0;
}

• b）当弹出数据后，使得队列头指针等于MAXQUEUE时，则队列头指针置0；修改后的 pop接口，代码实现如下：

QueueData& Queue::pop(){
     
    if (++front_ == MAXQUEUE) front_ = 0;
    if (front_ == 0)
        return data_[MAXQUEUE - 1];
    else
        return data_[front_ - 1];
}

• 但是，这样做存在一个问题，一旦压入数据的速度大于弹出数据的速度，并且队列中有效数据的个数大于 MAXQUEUE时，原有的数据会被下一次压入的数据覆盖掉，破坏原有内存结构，这个时候，循环队列已经不能解决问题，需要进行动态扩容了；

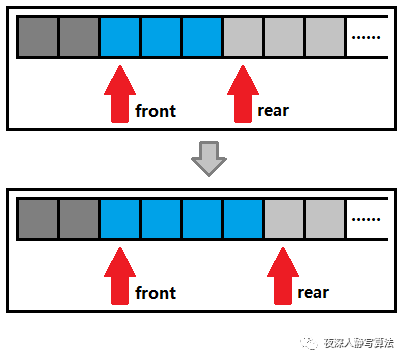
2）动态扩容

• 试想一下，对于一个循环队列，当 rear_ + 1 == front_时，再压入一个元素，就会导致rear_ == front_，队列就会变成空（参考上文的判空），这样就不能进行数据的弹出，导致队列不能正常运作，即使再压入数据，此时弹出的数据也不再是正确的，所以当队列剩余容量小于一定阈值的时候，我们需要把队列进行扩容处理；
• 队列剩余容量 T 的计算分两种情况：
• 当 front_ <= rear_时，T = MAXQUEUE - (rear_ - front_);
• 当 front_ > rear_时，T = front_ - rear_;
• 那么我们可以考虑，当 T < MAXQUEUE * 0.1时，开辟一块新的内存，内存大小为MAXQUEUE*2，将原有内存拷贝过去，并且修改 front_和rear_的值，然后再释放原有内存空间。
• 由于实际应用中，队列被用在网络消息的生产消费，基于多线程问题考虑，一般是需要加锁的，以上实现的是一个多线程不安全队列，关于加锁的内容不在本文讨论范围内。
• 以上就是有关队列的所有内容。

四、单向广搜的原理

• 为了更好的理解广搜的运作过程，我们需要先理解状态的概念。

1、状态的概念

1）状态

• 如果是计算机专业的同学，勉强上过几天编译原理的课，那么应该会对 有限状态自动机 这个词有点印象，没错，我们要说的状态就是它了。当然，为了照顾好逃课的同学，作者不会把书上的概念直接抄过来讲，毕竟那个太过于抽象，继续往下看，相信读者会对状态这个词有一个更加深入的理解。

2）状态转移

• 从一个状态到达另一个状态，这种转换的过程被称为状态转移。

图四-1-1

• 举个具体的例子，你现在的位置是 (1,3)，经过一步到达 (1, 4)，我们可以把 (1,3) 这个位置编号为 0，(1, 4) 这个位置编号为 1，那么可以称为你从 状态 0 到达了 状态 1，表示成 $(1,3)\to (1,4)$ 或者 $0\to 1$。
• 状态不仅仅可以表示位置，比如现在你的位置在 (1, 3) ，方向为向左，经过一次右转，位置不变但是方向变成了向上，这也是一种状态转移，即 $(1,3,left)\to (1,4,up)$。
• 从一个状态到达另一个状态的时候会有消耗，可以是 时间、精力、步数 等等。

3）初始状态 和 结束状态

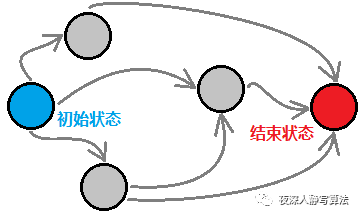
• 单向广搜的过程就是从 初始状态 通过穷举所有情况 最终到达 结束状态 的过程。而我们一般需要求的就是从 初始状态 到达 结束状态的最少时间（步数）。如图四-1-2描述的就是一个从初始状态经过一些中间状态，到达结束状态的过程。

图四-1-2

4）状态哈希

• 之前的章节已经学过哈希表，哈希表的目的是标记重复，这里的状态也是一样的道理。
• 因为在广搜的图上，有可能形成环，这样就会导致本来已经搜索到过的状态，被再次访问，而再次访问同一个状态是没有意义的，所以需要对访问过的状态进行标记，这就是状态哈希。

2、状态的程序描述

1）结构体定义

• 以【例题1】为例，我们需要的状态是一个二维坐标，即 主公 的位置。我们定义一个二维坐标来作为状态，于是可以把状态定义如下结构体BFSState：

struct Pos {
     
    int x, y;
    
    bool isInBound() {
     
        return !(x < 0 || y < 0 || x >= XMAX || y >= YMAX);
    }
    bool isObstacle() {
     
        return (Map[x][y] == MAP_BLOCK);
    }
};

struct BFSState {
     
    Pos p;
    ...
};

2）接口定义

• 状态的接口定义如下，先给出代码再进行讲解：

const int MAXSTATE = 1000000;

struct BFSState {
     
	...
public:
    inline bool isValidState();                   // 1）
    inline bool isFinalState();                   // 2）
    inline int getStep() const;
    inline void setStep(int step);
protected:
    int getStateKey() const;
public:
    static int step[MAXSTATE];                   // 3）
};

• 1）任何一个状态，都需要判断其合法性，比如对于迷宫来说，走出边界或者走到墙上都是非法状态，这个判定就是用 isValidState接口来完成的，实现可以是这样的：

bool BFSState::isValidState() {
     
    return p.isInBound() && !p.isObstacle();
}

• 当然，对于不同的问题，可以对这个接口进行重载；
• 2）当遇到结束状态的时候，我们需要停止搜索过程，所以就需要对一个状态进行判定，比如地图上公主的位置标识为 MAP_EXIT，那么就判断这个状态下的位置所在的地图格子是否是MAP_EXIT，实现如下：

bool BFSState::isFinalState() {
     
    return (Map[p.x][p.y] == MAP_EXIT);
}

• 3）getStep是用来获取初始状态到当前状态的最小步数，setStep是用来设置初始状态到当前状态的最小步数，因为实际情况的状态所对应的维数是不确定的，有的是一维，有的是二维，三维、四维、甚至更高维度的。为了将问题统一，我们需要做一层映射，即 多维状态向量 转换成 一维状态向量，这个转换的过程见下一节：状态的降维；
• 这里只需要知道getStateKey()获取的就是降维以后一维的状态编号，那么我们可以定义所有状态最小步数的存储结构为一维数组，即static int step[MAXSTATE];，设置和获取的接口定义如下：

int BFSState::getStep() const {
     
    return step[getStateKey()];
}
void BFSState::setStep(int sp) {
     
    step[getStateKey()] = sp;
}

3、状态的降维

• 对于状态，最后聊一下状态的降维；
• 1）K 进制：取一个相对较大的数字（所有状态的所有维度下都不会遇到的数字）定义为 K，然后按照一定的顺序将所有维度排列好，组织成一个 K 进制数，例如对于二维的情况，降维后的状态值 $state$ 就是：$$state=x\ast K^1+y\ast K^0$$
• 对应的代码实现如下：

int BFSState::getStateKey() const {
     
    return (p.x * K) + p.y;
}

• 2）位运算优化：如果找到一个 K 是 2 的幂，我们就可以采用位或和左移来优化这里的乘法了，例如：$K=2^6$，则：$$state=x<<6|y$$
• 对应的代码实现如下：

int BFSState::getStateKey() const {
     
    return p.x << 6 | p.y;
}

• 即 $y$ 占了二进制的低 6 位，$x$ 占了二进制的高 6 位。
• 3）映射预处理：当然还可以通过预处理的方式预先将所有的状态预先进行一一映射，如下代码代表的是将pos2State这个全局数组代表的二维状态转换成一维状态：

int stateId = 0;
for (int i = 0; i < K; ++i)
    for (int j = 0; j < K; j++)
            pos2State[i][j] = stateId++;

• 对应的代码实现如下：

int BFSState::getStateKey() const {
     
    return pos2State[p.x][p.y];
}

• 效率上来讲：映射预处理 > 位运算 > 乘法 （ > 代表优于）；

4、单向广搜的实现

• 如果对上面的状态相关的描述都已经理解了，那么单向广搜的内容基本也就清晰了，接下来我们来看下如何用队列来实现单向广搜。

1）广搜算法描述

单向广搜的算法大致可以描述如下：
  1）初始化所有状态的步数为无穷大，并且清空队列；
  2）将 起始状态 放进队列，标记 起始状态 对应步数为 0；
  3）如果队列不为空，弹出一个队列首元素，如果是 结束状态，则返回 结束状态 对应步数；否则根据这个状态扩展状态继续压入队列；
  4）如果队列为空，说明没有找到需要找的 结束状态，返回无穷大；

2）广搜算法框架

• 定义广搜图的接口如下：

class BFSGraph {
     
public:
    int  bfs(BFSState startState);
private:
    void bfs_extendstate(const BFSState& fromState);
    void bfs_initialize(BFSState startState);
private:
    Queue queue_;
};

• 其中 bfs作为一个框架接口供外部调用，基本是不变的，实现如下：

const int inf = -1;

int BFSGraph::bfs(BFSState startState) {
     
    bfs_initialize(startState);        // 1）
    while (!queue_.empty()) {
     
        BFSState bs = queue_.pop();    
        if (bs.isFinalState()) {
            // 2）
            return bs.getStep();
        }
        bfs_extendstate(bs);           // 3）
    }
    return inf;
}

• 1）初始化整个广搜的路径图，确保每个状态都是未访问状态；
• 2）如果队列不为空，则不断弹出队列中的首元素，如果是结束状态则直接返回状态对应的步数；
• 3）如果不是结束状态，对它进行状态扩展，扩展方式调用接口 bfs_extendstate，不同问题的扩展方式不同，下文会对不同问题的状态扩展进行讲解。

3）广搜算法初始化

• 对于广搜的初始化，调用bfs_initialize(startState)接口，主要做 4 件事情：
• 1）初始化所有状态为未访问状态；
• 2）清空队列；
• 3）设置 初始状态 的 步数为 0；
• 4）将 初始状态压入队列；
• 代码实现如下：

const int inf = -1;

void BFSGraph::bfs_initialize(BFSState startState) {
     
    memset(BFSState::step, inf, sizeof(BFSState::step));
    queue_.clear();
    startState.setStep(0);                      
    queue_.push(startState);
}

4）广搜算法的状态扩展

• 广搜的状态扩展比较多样化，这里介绍一种四方向迷宫类的问题的扩展方式，如图四-4-1所示：

图四-4-1

• 首先需要定义四个方向常量，如下：

const int dir[DIR_COUNT][2] = {
     
    {
      1, 0 },  // 下
    {
      0, 1 },  // 右
    {
      0, -1 }, // 左
    {
      -1, 0 }  // 上
};

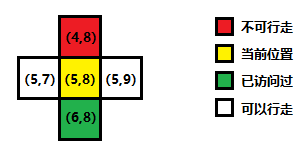
• 当前位置为 (5, 8)，除了一个不可行走的墙体 (4, 8) ，已经访问过的 (6, 8) 以外，其它两个格子是可以被访问的，那么将它们加入队列，则状态扩展完毕后，队列中的数据如图四-4-2所示：

图四-4-2

• (5, 8) 是当前位置，已经弹出队列，(5, 9) 和 (5, 7) 按照枚举方向的顺序，加入队列中；
• 对于四方向迷宫类问题的状态扩展的代码实现如下：

void BFSGraph::bfs_extendstate(const BFSState& fromState) {
     
    int stp = fromState.getStep() + 1;            // 1）
    BFSState toState;
    for (int i = 0; i < DIR_COUNT; ++i) {
     
        toState.p = fromState.p.move(i);          // 2）
        if (!toState.isValidState() || toState.getStep() != inf) {
                 
            continue;                             // 3）
        }
        toState.setStep(stp);                     // 4）
        queue_.push(toState);
    }
}

• 1）本文介绍的广搜都是任意两个状态之间权值相同的情况，权值不同的情况需要用到 SPFA 算法来求最短路，会在后续的章节中继续展开，所以这种问题下两个状态之间的步数为 1（即权值）。
• 2）扩展状态的时候，从前一个状态经过某个方向走了一步，用 move来实现，我们可以对 Pos结构体进行一个扩展，如下：

struct Pos {
     
    ... 
    Pos move(int dirIndex) const {
     
        return Pos(x + dir[dirIndex][0], y + dir[dirIndex][1]);
    }
};

• 其中dir[][]代表的是一个方向向量，用于实现move接口的向量相加；
• 3）当判断到达的状态是一个非法状态（图四-4-1中的红色方块）、或者曾经已经访问过（图四-4-1中的绿色方块）的话，则不进行压队操作，继续下一个方向的扩展；
• 4）否则，表明当前扩展状态是合法状态（图四-4-1中的白色方块），标记访问步数，将扩展的状态压入队列；

五、单向广搜的应用场景

1、迷宫问题

1）双人迷宫

【例题2】给定一个 $n\times m(n,m<=20)$ 的迷宫，有些格子是墙体不能进入，迷宫中有一个 主公 和 一位 公主，主公每次可以选择上、下、左、右四个方向进行移动，每次主公移动的同时，公主可以按照相反方向移动一格（如果没有墙体遮挡的话）。当主公和公主相邻或者进入同一个格子则算游戏结束，问至少多少步能让游戏结束。

• 这个问题和【例题1】的区别就是公主变成了动态的，而且是跟随主公的脚步进行移动，所以在设计状态的时候需要考虑公主的状态。所有动态的对象都应该被设计到状态里，所以这个问题的状态就是 主公 和 公主 两个人的位置。
• 设计状态如下：

struct BFSState {
     
    Pos p[2];
    ...
};

• 其中 $p[0]$ 代表主公的位置，$p[1]$ 代表公主的位置。结束状态是两个人坐标的曼哈顿距离小于等于 1，即：

bool BFSState::isFinalState() {
     
    return abs(p[0].x - p[1].x) + abs(p[0].y - p[1].y) <= 1;
}

• 然后只需要枚举主公的四方向进行广搜就行了。

2）推箱子

【例题3】给定一个 $n\times m(n,m<=8)$ 的迷宫，上面有 $x(x<=4)$ 个箱子 和 1个人，以及一些障碍和箱子需要放置的最终位置，求一种方案，用最少步数将所有的箱子推到指定位置。

图五-1-1

• 图五-1-2 是我们最重要实现的效果：
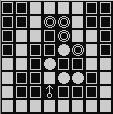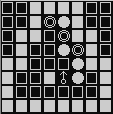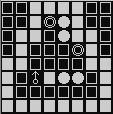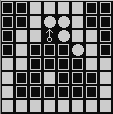
  图五-1-2
• 算法的焦点一定在这个 “小人” 身上，但是光用 “小人” 的位置来表示状态肯定是不够的；
• 如图五-1-3所示，两个地图关卡的小人的位置是相同的，但是不能作为同一种情况来考虑，因为箱子的位置不同，所以最终状态表示也不同。根据【例题2】的经验，所有动态的对象都应该被设计到状态里。
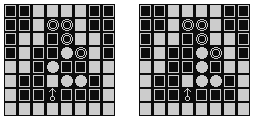
  图五-1-3
• 所以应该拿 小人 和 四个箱子 的位置来作为状态，设计如下：

struct BFSState {
     
    Pos man, box[4];
    ...
};

• 然后针对这个问题需要考虑几个点：
• 1）状态数太大：每个坐标的最大值为7，需要用 8 进制表示状态，总共 10 位，即 $8^{10}=1073741824$。
• 2）箱子的无差别性：由于四个箱子被认为是一样的，所以对于两组箱子的状态，位置重排后一一对应的应该被认为是同样的状态，例如： $[(1,1),(1,2),(2,4),(4,5)]$ 和 $[(4,5),(1,1),(1,2),(2,4)]$ 是同一个状态。
• 3）非法状态：所有墙体的位置都应该被计算为非法状态。
• 基于以上三点，我们可以对状态进行压缩，减少状态空间，首先用 小人 做一次连通性搜索，标记所有能够到达的点，然后进行编号，如图五-1-4所示：
  图五-1-4
• 这样一来每个坐标只需要用一个 小于 24 的数来表示，也就是 $24^5=7962624$，即最大的状态编号。
• 然而实际上，基于四个箱子的无差异性，这是一个组合问题，不是排列问题，并且由于箱子和人都不能重叠，对于这个关卡来说，23 个空位置，选出 4 个位置放箱子，再从 19 个位置选择 1 个放小人，所以总的状态数是：
  $$C_{23}^4{C}_{19}^1=4037880$$
• 由于实际状态数会明显少很多（比如当某个箱子被推到墙角以后就无法再扩展状态），所以对于得到的状态编号我们可以进行一层散列哈希，用一个更小的数组来进行标记节省内存。
• 最后，结束状态 就是 所有箱子都到指定位置，当然，这个问题中结束状态有多个，因为箱子虽然归位了，小人的位置是可以任意选择的。

3）右转迷宫

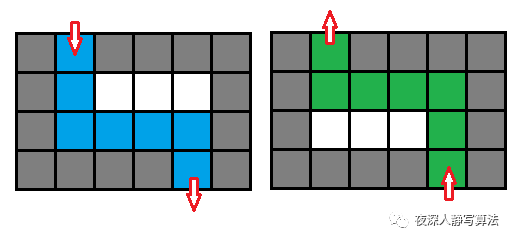
【例题4】给定一个 $n\times m(n,m<=500)$ 的迷宫，一个入口一个出口。走迷宫的规则是优先选择右边的方向走，如果右边有墙就往前走，如果还有墙就往左，如果还有就掉头，问从入口到出口，以及出口到入口，能否将整个迷宫的区域走遍。如图5就是一种可行方案。

图五-1-5

• 这个问题的动态对象只有一个，但是光用一个人的位置来表示状态肯定是不够，考虑 图五-1-6 的这种情况：
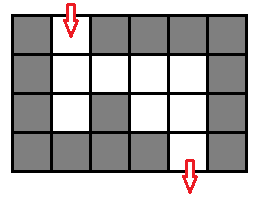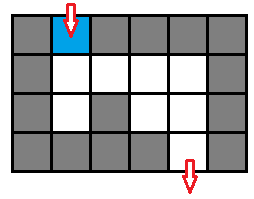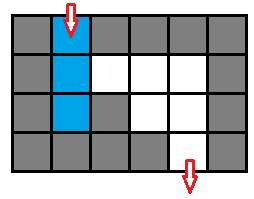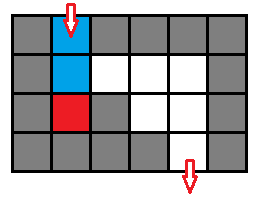
  图五-1-6
• 如果只用位置来标记状态，那么遇到一个三面都是墙的位置就要回头，但是回头的时候发现状态已经被标记过了，所以就不会继续扩展状态，导致搜索提前结束。
• 那么这里的改善方式就是在状态中加入一个方向的维度，即：

struct BFSState {
     
    Pos p;
    char dir;
    ...
};

• 这样一来，对于同一个格子的 前进 和 回头 就不是同一个状态了。

4）收集物品

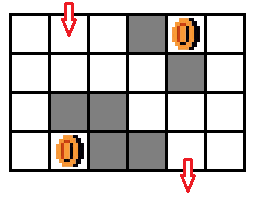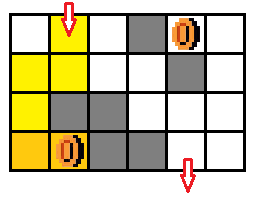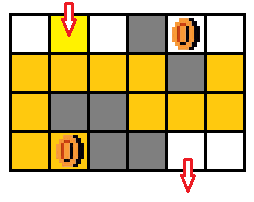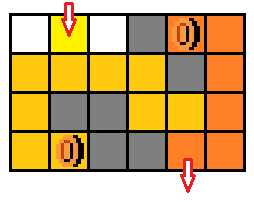
【例题5】给定一个 $n\times m(n,m<=20)$ 的迷宫，一个入口一个出口。并且有 $x(x<=10)$ 个金币，问从入口到出口并且收集到所有 x 的最少时间。

图五-1-7

• 在每个位置上，没有拿到金币和拿到金币的状态是不一样的（从图五-1-7中可以看出，黄色、金黄色、橙色 的三种路径分别表示没有取得金币，取得一个金币，取得两个金币的情况）。那么将所有金币组合一下，总共有 $2^x$ 种状态，所以状态就是坐标和金币的组合态，即：

struct BFSState {
     
    Pos p;
    int coinMask;
    ...
};

• 其中 coinMask 是一个二进制数，它的第 $k(0<=k<x)$ 位 代表第 $k$ 个金币有没有获得，那么结束状态就是坐标等于出口，并且 coinMask 为 $2^x-1$。

5）贪吃蛇

【例题6】一个 $n\times m(n,m<=20)$ 的迷宫，左上角 (0, 0) 为出口，一条蛇在迷宫中，蛇的身体长度为 L，最多占用 8 个格子，有上下左右四个方向可以走，蛇走的时候不能碰到自己的身体，问最少需要多少步才能走到出口。

图五-1-8

• 首先蛇的身体长度为 8，也就是如果把所有身体占用的格子作为状态，就是 $400^8$，这样就很恐怖了。
• 但是仔细分析一下，因为身体是连在一起的，所以只要头部确定，第二节身体格子的方向最多4种，后面每个身体格子的方向最多3种，所以总的状态数是 $20\ast 20\ast 4\ast 3^6=1166400$，状态表示如下：

struct BFSState {
     
    Pos p;
    int dir[7];
    ...
};

• 由于方向数目为四个，所以我们可以把每个身体的方向用一个四进制的数来表示，$4^7=2^{14}$ 在 32 位整数范围内，所以状态表示可以变成：

struct BFSState {
     
    Pos p;
    int dirMask;
    ...
};

• 和金币问题类似，采用二进制进行位压缩；

2、同余搜索

【例题7】给定一个不能被 2 或 5 整除的数 $n(0<=n<=10000)$，求一个十进制表示都是 1 的数 $K$ ，使得 $K$ 是 $n$ 的倍数，且最小。例如：$n=3$，那么答案就是 111，因为 $111\mathrm{m}\mathrm{o}\mathrm{d}3=0$。

• 模拟 1 个 1，2 个 1, 3 个 1 … 不断对 $n$ 取余数，根据初等数论的知识，我们令 $a[i]$ 表示 $i$ 个 1 对 $n$ 取余数的值，则有：$$a[i]=(a[i-1]\ast 10+1)\mathrm{m}\mathrm{o}\mathrm{d}n$$
• 那么当某个 $a[i-1]$ 出现过了，后面的 $a[i]$ 势必也会重复，所以我们可以拿 $a[i]$ 作为状态，结束状态就是找到 $a[...]=0$， 这样最多进行 10000 次枚举就能找到满足条件的状态。

3、预处理

• 这里介绍的是一种思想，适用于数据量很大的问题。
• 对于一些 结束状态 永远是固定的，而 初始状态 不同，并且询问很多 的问题，那么我们可以从 结束状态 开始搜索，并且将到达的所有状态都一次性搜索出来，那么，每次询问的时候只需要查询状态步数即可，总时间复杂度就是预处理的时间，查询时间复杂度 $O(1)$。

---

本文所有示例代码均可在以下 github 上找到：github.com/WhereIsHeroFrom/模板/广度优先搜索

---

---

六、单向广搜题集整理

题目链接	难度	解法
PKU 1096 Space Station Shielding	★☆☆☆☆	FloodFill
HDU 2952 Counting Sheep	★☆☆☆☆	FloodFill
HDU 1026 Ignatius and the Princess I	★☆☆☆☆	优先队列应用
HDU 1072 Nightmare	★☆☆☆☆	记录时间维度
HDU 1240 Asteroids!	★☆☆☆☆	【例题1】三维迷宫
HDU 1415 Jugs	★☆☆☆☆	经典广搜 - 倒水问题
HDU 1495 非常可乐	★☆☆☆☆	经典广搜 - 倒水问题
HDU 1195 Open the Lock	★☆☆☆☆	一维的数码可达问题
PKU 1915 Knight Moves	★★☆☆☆	马的走位
HDU 1372 Knight Moves	★★☆☆☆	马的走位
HDU 2235 机器人的容器	★★☆☆☆	FloodFill
HDU 3713 Double Maze	★★☆☆☆	2个人的迷宫问题
HDU 2216 Game III	★★☆☆☆	【例题2】2个人的迷宫问题
HDU 3309 Roll The Cube	★★☆☆☆	2个人的迷宫问题
HDU 1254 推箱子	★★☆☆☆	【例题3】推箱子问题
PKU 1475 Pushing Boxes	★★☆☆☆	【例题3】推箱子问题
HDU 1253 胜利大逃亡	★★☆☆☆	三维迷宫
HDU 1252 Hike on a Graph	★★☆☆☆	3个人的迷宫问题
HDU 1044 Collect More Jewels	★★☆☆☆	【例题5】二进制状态压缩的应用
PKU 2157 Maze	★★☆☆☆	二进制状态压缩的应用
HDU 3220 Alice’s Cube	★★☆☆☆	预处理 + 位运算
HDU 1429 胜利大逃亡(续)	★★☆☆☆	二进制状态压缩的应用
PKU 1077 Eight	★★☆☆☆	经典八数码
HDU 2170 Frogger	★★☆☆☆	带停留的搜索
HDU 1226 超级密码	★★☆☆☆	枚举位数
PKU 2551 Ones	★★☆☆☆	同余搜索
PKU 1426 Find The Multiple	★★☆☆☆	同余搜索
PKU 1860 Currency Exchange	★★☆☆☆	SPFA
PKU 1237 The Postal Worker Rings	★★☆☆☆	SPFA
PKU 1724 ROADS	★★☆☆☆	优先队列应用
HDU 2822 Dogs	★★☆☆☆	优先队列应用
HDU 2851 Lode Runner	★★☆☆☆	优先队列应用
HDU 2237 无题III	★★☆☆☆	多维状态搜索
HDU 3912 Turn Right	★★☆☆☆	【例题4】右转迷宫 + 增加方向维度
PKU 2283 Different Digits	★★★☆☆	同余搜索
PKU 2206 Magic Multiplying Machine	★★★☆☆	同余搜索
HDU 1104 Remainder	★★★☆☆	同余搜索
PKU 3000 Frogger	★★★☆☆	同余搜索
HDU 1317 XYZZY	★★★☆☆	最长路判环
HDU 1384 Intervals	★★★☆☆	差分约束
HDU 1531 King	★★★☆☆	差分约束
PKU 1716 Integer Intervals	★★★☆☆	差分约束
PKU 3501 Escape from Enemy Territory	★★★☆☆	二分答案 + BFS
PKU 1292 Will Indiana Jones Get	★★★☆☆	二分答案 + BFS
PKU 1485 Fast Food	★★★☆☆	SPFA
PKU 1511 Invitation Cards	★★★☆☆	SPFA
PKU 1545 Galactic Import	★★★☆☆	SPFA
PKU 1734 Sightseeing trip	★★★☆☆	无向图最小环
PKU 1420 Spreadsheet	★★★☆☆	建立拓扑图后广搜
PKU 2353 Ministry	★★★☆☆	需要存路径
PKU 2046 Gap	★★★☆☆	A*
PKU 1778 All Discs Considered	★★★☆☆
PKU 1097 Roads Scholar	★★★☆☆	SPFA
PKU 1324 Holedox Moving	★★★☆☆	【例题6】状态压缩的广搜
PKU 1062 昂贵的聘礼	★★★☆☆	优先队列应用
PKU 3897 Maze Stretching	★★★☆☆
PKU 3346 Treasure of the Chimp	★★★☆☆
PKU 2983 Is the Information Reliable	★★★☆☆	最长路判环
PKU 1482 It’s not a Bug, It’s a	★★★☆☆
HDU 3008 Warcraft	★★★☆☆
HDU 3036 Escape	★★★☆☆
PKU 3322 Bloxorz I	★★★☆☆	当年比较流行这个游戏
HDU 1043 Eight	★★★☆☆	数据较强，需要预处理
HDU 1307 N-Credible Mazes	★★★☆☆	多维空间搜索，散列HASH
HDU 3681 Prison Break	★★★☆☆	状态压缩
HDU 3500 Fling	★★★☆☆	某个消除游戏
HDU 2605 Snake	★★★★☆	状态压缩
HDU 1122 Direct Visibility	★★★★☆	计算几何判断连通性
PKU 3912Up and Down	★★★★☆	离散化 + BFS
PKU 3463 Sightseeing	★★★★☆	SPFA
PKU 3328 Cliff Climbing	★★★★☆	日本人的题就是这么长
PKU 3455 Cheesy Chess	★★★★☆	仔细看题
PKU 1924 The Treasure	★★★★☆
PKU 3702 Chessman	★★★★★	弄清状态同余的概念
HDU 3278 Puzzle	★★★★★	几乎尝试了所有的搜索 -_-
HDU 3900 Unblock Me	★★★★★	8进制压缩状态，散列HASH，位运算加速