夜深人静写算法（十七）- 分组背包

一、前言

  你是否曾经迷茫过？“为什么算法这么难？”
  是的，作者也曾经迷茫过，但是每当通过自己的意识理解了一个算法，之前熬过的苦都烟消云散了，为什么金字塔尖上的人这么少，就是因为他们能忍常人所不能忍，吃常人所不能吃的苦，终成大业！所以，天下无易成之业，亦无不可成之业，各守乃业，则业无不成。
  当你觉得坚持不下去的时候，千万不要心浮气躁，出去跑跑步，刷刷水题，找回一点信心，及时给自己一些正反馈，有了信心，何愁大业不成！所谓正反馈，就是你做的时候有点小开心，本质上就是对爱好的一种改造，就像 夜深人静 的时候写算法一样 Hiahiahia…！

二、分组背包问题

• 今天要讲的分组背包问题，其中包含了 0/1 背包的思想，如果读者对 0/1 背包还没有很深入的理解，建议回去复习一下 0/1 背包问题，这一章内容本身较为简单，但是由它衍生的出来的问题，并不是很容易，所以一定要深刻理解状态转移方程的含义，而不是死记硬背。那么，接下来，还是通过一个例题来阐述下分组背包的含义。

【例题1】有 $n(n<=1000)$ 个物品和一个容量为 $m(m<=1000)$ 的背包。这些物品被分成若干组，第 $i$ 个物品属于 $g[i]$ 组，容量是 $c[i]$，价值是 $w[i]$，现在需要选择一些物品放入背包，并且每组最多放一个物品，总容量不能超过背包容量，求能够达到的物品的最大总价值。

• 以上就是分组背包问题的完整描述，和其它背包问题的区别就是每个物品多了一个组号，并且相同组内，最多只能选择一个物品放入背包；因为只有一个物品，所以读者可以暂时忘掉 完全背包 和 多重背包 的概念，在往下看之前，先回忆一下 0/1 背包的状态转移方程。

1、预处理

• 第一步：预处理；
• 首先把每个物品按照组号 $g[i]$ 从小到大排序，假设总共有 $t$ 组，则将 $g[i]$ 按顺序离散到 $[1,t]$ 的正整数；
• 这样做的目的是为了将 $g[i]$ 作为下标映射到状态数组中；
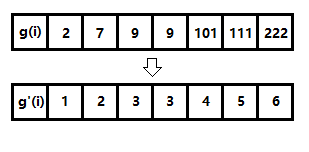
  图二-1-1

2、状态设计

• 第二步：设计状态；
• 状态 $(k,j)$ 表示前 $k$ 组物品恰好放入容量为 $j$ 的背包 $(k\in [0,t],j\in [0,m])$；
• 令 $dp[k][j]$ 表示状态 $(k,j)$ 下该背包得到的最大价值，即前 $k$ 组物品（每组物品至多选一件）恰好放入容量为 $j$ 的背包所得到的最大总价值；

3、状态转移方程

• 第三步：列出状态转移方程：$$dp[k][j]=max(dp[k-1][j],dp[k-1][j-c[i]]+w[i])$$ $$k=g[i]$$
• 因为每个物品有只有两种情况：
• 1）不放：如果 “第 $i$ 个物品（属于第 $k$ 组）不放入容量为 $j$ 的背包”，那么问题转化成求 “前 $k-1$ 组物品放入容量为 $j$ 的背包” 的问题；由于不放，所以最大价值就等于 “前 $k-1$ 组物品放入容量为 $j$ 的背包” 的最大价值，对应状态转移方程中的 $dp[k-1][j]$；
• 2）放：如果 “第 $i$ 个物品（属于第 $k$ 组）放入容量为 $j$ 的背包”，那么问题转化成求 “前 $k-1$ 组物品放入容量为 $j-c[i]$ 的背包” 的问题；那么此时最大价值就等于 “前 $k-1$ 组物品放入容量为 $j-c[i]$ 的背包” 的最大价值 加上放入第 $i$ 个物品的价值，即 $dp[k-1][j-c[i]]+w[i]$；
• 因为 前 $k-1$ 组物品中一定不存在第 $k$ 组中的物品，所以能够满足 “最多放一个” 这个条件；

4、时间复杂度分析

• 对于 $n$ 个物品放入一个容量为 $m$ 的背包，状态数为 $O(nm)$，每次状态转移的消耗为 $O(1)$，所以整个状态转移的过程时间复杂度是 $O(nm)$；
• 注意在分组背包求解的时候，要保证相同组的在一起求，而一开始的预处理和离散化正式为了保证这一点，这样，每个物品的组号为 $g[i]=1,2,3,4...,t$，并且我们可以把状态转移方程进一步表示成和 $k$ 无关的，如下：$$dp[g[i]][j]=max(dp[g[i]-1][j],dp[g[i]-1][j-c[i]]+w[i])$$

三、分组背包问题的优化

• 时间复杂度已经无法优化，那么空间复杂度是否可以像 0/1 背包 那样进行降维呢？

1、空间复杂度优化

• 考虑前 $k$ 组的状态依赖前 $k-1$ 组的子结果，所以第一层循环应该是枚举 “组”；
• 然后我们尝试将 “组” 那一维的状态去掉，得到状态转移方程如下：$$dp[j]=max(dp[j],dp[j-c[i]]+w[i])$$
• 考虑这里的物品最多只能取 1 个，类似 0/1 背包，所以容量枚举需要采用逆序；
• 这时候，我们把物品枚举放外层，容量枚举放内层，会发现变成了第 $k$ 组内的 0/1 背包问题，而这不是我们想要的，我们要求一个组内只能最多取一个物品。所以调整顺序：容量枚举放外层，物品枚举放内层。
• 于是，得到了一个降维后的算法，三层循环：枚举组 $1\to t$、 枚举容量 $m\to 0$、枚举组内物品 $i$；
• 给出伪代码如下：

for (每个组 k = 1 -> t) {
     
    for (容量 j = m -> 0) {
     
        for (每个组内的物品 i) {
     
            dp[j] = opt(dp[j], dp[j - c[i]] + w[i]);
        }
    }
}

• C++ 代码实现如下：

int groupKnapsack(int knapSize, Knapsack *knap, int m) {
     
    groupKnapsackInit(m);
    int t = groupKnapsackRegroup(knapSize, knap);
    for (int k = 1; k <= t; ++k) {
     
        for (int j = m; j >= 0; --j) {
     
            for (int i = 0; i < GKnap[k].size(); ++i) {
     
                const Knapsack &item = GKnap[k].get(i);
                if (j >= item.capacity) {
     
                    dp[j] = opt(
                        dp[j],
                        dp[j - item.capacity] + item.weight
                    );
                }
            }
        }
    }
    return t;
}

• groupKnapsackInit用于初始化状态数组，groupKnapsackRegroup则是对物品进行分组的过程；
• 定义分组背包的数据结构如下，核心是用一个线性表来存储同一组背包物品，代码比较简单就不解释了：

struct GroupKnapsack {
     
    vector <Knapsack> items;
    void clear() {
     
        items.clear();
    }
    void add(const Knapsack& knap) {
     
        items.push_back(knap);
    }
    int size() const {
     
        return items.size();
    }
    int getGroupId() {
     
        if (size()) {
     
            return items[0].groupId;
        }
        return -1;
    }
    const Knapsack& get(int idx) const {
     
        return items[idx];
    }
}GKnap[MAXN];

四、分组背包的应用及变种

1、每组至少一个

【例题2】有 $n(n<=1000)$ 个物品和一个容量为 $m(m<=1000)$ 的背包。这些物品被分成若干组，第 $i$ 个物品属于 $g[i]$ 组，容量是 $c[i]$，价值是 $w[i]$，现在需要选择一些物品放入背包，并且每组至少选择一个，总容量不能超过背包容量，求能够达到的物品的最大总价值。

• 同样，先进行分组，组号 $g[i]$ 相同的放在一组；
• 令 $dp[k][j]$ 表示前 $k$ 组物品（每组物品至少选一件）恰好放入容量为 $j$ 的背包所得到的最大总价值；
• 先给出状态转移方程：$$dp[k][j]=max(dp[k][j],dp[k-1][j-c[i]]+w[i],dp[k][j-c[i]]+w[i])$$ $$k=g[i]$$
• 对于这个状态转移方程，我们可以分成两部分来解读：
• 1）组内：0/1 背包问题：也就是状态转移方程中的这部分：$$dp[k][j]=max(dp[k][j],dp[k][j-c[i]]+w[i])$$
• 它的含义是：在同一组中，每个物品的 选 与 不选 没有限制，$dp[k][j]$ 表示没有选第 $k$ 组的 $i$ 这个物品的最大价值；$dp[k][j-c[i]]+w[i]$ 表示选了第 $k$ 组的 $i$ 这个物品的最大价值（细心的读者会发现，这个状态转移方程去掉 $k$ 这一维正是 0/1 背包降维以后的状态转移方程）；
• 2）组间：至少1个：只要保证 上一组 的状态到 当前组 的状态进行状态转移的时候，至少放一个物品就行了。换言之，状态 $dp[k-1][j]$ 不能转移到状态 $dp[k][j]$， 所以我们得到至少放一个的状态转移方程，如下：$$dp[k][j]=max(dp[k][j],dp[k-1][j-c[i]]+w[i])$$
• 将以上两个状态转移方程进行合并，就是我们一开始给出的状态转移方程了。
• 求解顺序也是三层循环：枚举组 $1\to t$、 枚举组内物品 $i$、枚举容量 $m\to c[i]$；

for (每个组 k = 1 -> t) {
     
    for (容量 j = 0 -> m) {
     
        dp[k][j] = inf;
    }
    for (每个组内的物品 i) {
     
        for (容量 j = m -> c[i]) {
     
            dp[k][j] = opt(dp[k][j], dp[k - 1][j - c[i]] + w[i], dp[k][j - c[i]] + w[i]);
        }
    }
}

• 因为要保证组内 0/1 背包，所以内层的两层循环正好是 0/1 背包的枚举顺序；
• C++ 代码实现如下：

int groupKnapsack(int knapSize, Knapsack *knap, int m) {
     
    groupKnapsackInit(m);
    int t = groupKnapsackRegroup(knapSize, knap);
    for (int k = 1; k <= t; ++k) {
     
        for (int j = 0; j <= m; ++j) {
     
            dp[k][j] = inf;
        }
        for (int i = 0, s = GKnap[k].size(); i < s; ++i) {
     
            const Knapsack &item = GKnap[k].get(i);
            for (int j = m; j >= item.capacity; --j) {
     
                dp[k][j] = opt(
                    dp[k][j],
                    dp[k][j - item.capacity] + item.weight,
                    dp[k - 1][j - item.capacity] + item.weight
                );
            }
        }
    }
    return t;
}

2、每组正好一个

• “正好选择一个” 和 “最多选择一个” 类似，我们首先来回顾下 “最多选择一个” 的状态转移方程：$$dp[k][j]=max(dp[k-1][j],dp[k-1][j-c[i]]+w[i])$$ $$k=g[i]$$
• 这里的 $dp[k-1][j]$ 对应的就是当前枚举的物品不放的情况，如果要求 “正好选择一个”，也就是不能出现不放的情况，所以只需要将这种情况去掉就可以了，得到状态转移方程如下：$$dp[k][j]=max(dp[k-1][j-c[i]]+w[i])$$
• 通过一个例题来加深理解。

【例题3】一架天平，$C(C<=20)$ 个钩子，$G(G<=20)$ 个砝码。每个钩子的范围 $[-15,15]$，每个砝码的重量范围是 $[1,25]$，问将每个砝码放上对应的钩子，最后使得天平平衡的方案数。

• 首先我们要知道天平平衡条件为： 天平两边力矩绝对值相等，而 力矩 = 力臂 * 重量；
• 每个砝码 $\times$ 每个位置 得到一个 力矩（注意有正负），所以对于每个砝码，有 $C$ 种选择；
• 假设 20 个砝码值均为 25，都放在最边缘，得到最大力矩为 15 * 20 * 25 = 7500，负力矩就是 -7500，所以可以设定一个 7500 的偏移量，背包最大容量设为 15010 （10为容错值）。
• 然后就是对每个砝码组进行正好选 1 个的分组背包了。容量有正负，所以无论顺序还是逆序枚举都有问题，最好的解决办法就是采用滚动数组。
• 参照正好选择一个，得到状态转移方程为：$$dp[cur][j]=sum(dp[last][j-c[i]])$$
• 这个问题让我们了解到了物品的分组是可以自行建立的，接下来我们来看看将几种背包物品进行混合会是什么样的情况。

3、混合分组背包问题

【例题4】给出 $n,T(0<=n<=T)$，代表 $n$ 个集合的工作要求在 $T$ 分钟内完成，每个工作集合包含三种类型：
  1）类型 0 代表这个集合里面的工作至少要选择一项去做；
  2）类型 1 代表这个集合里面的工作至多选择一项去做；
  3）类型 2 代表集合里面的工作可以自由选择；
每个集合的工作包含 $m(m<=100)$ 对值 $(0<=c[i],g[i]<=100)$，代表工作消耗的时间 和 获得的快乐度，每个工作只能选择一次，求获得的最大快乐度，如果无法完成给定要求输出 -1；

• 对于三种类型的工作集合中的每个工作，在一个容量背包上处理，为了降低空间复杂度，并且权衡思考复杂度，采用滚动数组进行状态转移。用 $dp[2][T]$ 来记录状态，$dp[cur][i]$ 表示枚举当前组时容量为 $i$ 的最大快乐度，$dp[last][i]$ 表示前面的组容量为 $i$ 的最大快乐度；

1）类型2：0/1 背包

• 对于类型为 2 的，选择没有限制的，就是最简单的 0/1 背包问题，按照 0/1 背包的状态转移方程求解：$$dp[cur][j]=max(dp[cur][j],dp[last][j-c_k]+g_k)$$
• 当前组的每个物品选择和不选择两种情况；

2）类型1：至多1个的分组背包

• 对于类型为 1 的，至多选择一项，状态转移如下：$$dp[cur][j]=max(dp[cur][j],dp[last][j],dp[last][j-c_k]+g_k)$$
• 用上一组的背包来尝试装载这一组的每个物品的情况：
• 2.a）$dp[last][j]$ 表示这一组的第 $k$ 个物品不选的情况；
• 2.b）$dp[last][j-c_k]+g_k$ 表示这一组的第 $k$ 个物品选的情况；

3）类型0：至少1个的分组背包

• 对于类型为 0 的，至少选择一项，状态转移如下：$$dp[cur][j]=max(dp[cur][j],dp[cur][j-c_k]+g_k,dp[last][j-c_k]+g_k)$$
• 用上一组 以及 这一组 的背包来尝试装载这一组的每个物品的情况：
• 3.a）$dp[cur][j]$ 表示这一组的第 $k$ 个物品不选的情况；
• 3.b）$dp[cur][j-c_k]+g_k$ 表示这一组的第 $k$ 个物品选的情况；
• 3.c）$dp[last][j-c_k]+g_k$ 表示这一组的第 $k$ 个物品是第一个被选进来的情况，所以要从上一个组的背包进行转移；
• 这个是比较经典的混合背包问题，读者可以思考下如果再引入完全背包，多重背包，该如何求解？
• 接下来我们来看看和数论相结合的分组背包问题，这些问题连物品都没有，需要我们根据条件自行创建一些物品，并且分组进行求解。

4、结合数论的分组背包问题

【例题5】将 $S(S<=1000)$分解成若干个数，并且得到它们的最小公倍数 $x$，问 $x$ 可能有多少种情况。

• 如果将 $S$ 分解成 $n$ 个数 $a_i(0\le i<n)$，它们的最小公倍数为 $L=lcm(a_1,a_2,...,a_n)$；
• 根据算术基本定理，$L$ 一定可以表示成素数幂的乘积的形式：$$L=2^{e_2}{3}^{e_3}...2999^{e_{2999}}$$
• $a_i$ 中素数 $p$ 的个数为 $c_p[i]$，则 $e_p={\max }_{i=0}^{n-1}(c_p[i])$；
• 对于 $e_p$ 来说，我们只关心 $a_i(0\le i<n)$ 中素因子 $p$ 最多的那个数，其它没有任何贡献，所以问题可以等价成将 $S$ 拆分成 $n$ 个素数幂的和的方案数，每个素数可以取 0次、1次、2次 …；
• 而每个素数取 0次、1次、2次 …，相乘后得到的数字必然不同，这个是由算数基本定理决定的。所以计算得到的方案数也就是最后结果的方案数，那么所有 1000 以下的素数 $p$ 的次幂 $p、p^2、p^3、...p^t$ 看成一个组，作为背包物品，容量为 $p^k$，做一次每组最多取 1 个的分组背包，用 $dp[k][j]$ 表示状态，即前 $k$ 组素数幂组合得到的和为 $j$，最小公倍数的方案数为 $dp[k][j]$，状态转移方程为：$$dp[k][j]=dp[k-1][j]+dp[k-1][j-p^i]$$
• 初始状态为：$dp[0][0]=1$；
• 小于 1000 的素数个数为 $K$，最后的答案为 ${\sum }_{j=0}^{S}dp[K][j]$。

【例题6】将 $S(S<=3000)$ 分解成若干个数，并且保证这些数的最小公倍数最大，求这个最大乘积模上 $M$ 的值。

• 沿用【例题5】的思路，根据算术基本定理，这些数的乘积 $L$ 一定可以表示成素数幂的乘积的形式：$$L=2^{e_2}{3}^{e_3}...2999^{e_{2999}}$$
• 将等式左右两边同时取以 $2$ 为底的对数，等式不变，如下：
  $$\begin{array}{rl}lo{g}_{2}L& =lo{g}_2(2^{e_2}{3}^{e_3}...2999^{e_{2999}})\\ & =e_{2}lo{g}_{2}2+e_{3}lo{g}_{2}3+...+e_{2999}lo{g}_{2}2999\end{array}$$
• 由于函数 $y=lo{g}_2(x)$ 是个增函数，所以要求 $L$ 最大，就是求 $lo{g}_{2}L$ 最大。
• 然后我们再来分析等式右边的部分，都是形如 $e_{p}lo{g}_{2}p$ 的乘积形式，其中 $lo{g}_{2}p$ 是常量，$e_p$是变量，把 $e_p$ 展开得到：$$e_p=\underset{i=0}{\overset{n-1}{\max }}(c_p[i])=\max (c_p[0],c_p[1],...,c_p[n-1])$$
• 我们发现，当 $e_p=c_p[k]$，并且对于 $i$ 不等于 $k$ 时 $c_p[i]=0$，这种情况一定是最优的；
• 因为我们可以把 $e_{p}lo{g}_{2}p$ 看成是背包物品的价值，$p^{e_p}$ 看成是背包物品的容量，上面的做法可以保证相同价值的情况需要的容量最少。
• 于是，我们得出一个算法如下：

1）筛选出 $3000$ 以下所有素数，总共 P 个素数；
2）对小于 $3000$ 的素数次幂 $p、p^2、p^3、...p^k$ 分成一组，作为背包物品，容量为 $p^k$，价值为 $klo{g}_{2}p$；
3）做一次每组最多取 1 个的分组背包，记录路径；
4）从 $dp[P][1...S]$ 中取最优解，然后进行路径回溯，回溯过程进行幂取模操作；

五、分组背包总结

• 以上就是本文关于 分组背包 的所有内容。
• 分组背包的状态转移方程是模板，没有太大变数，但是难就难在物品不是事先分好组的，而是需要根据问题本身去建立分组，甚至有时候连物品都没有，而是一些隐式的数字，需要通过问题给的条件去提取出容量和价值，例如上文提到的和数论结合的分组背包问题，需要读者仔细去理解和体会。
• 如果对分组背包没有完全理解，建议自己多推敲一下它的状态转移方程，它将会是 树上分组背包、依赖背包、树形 DP 的基础。

---

• 本文所有示例代码均可在以下 github 上找到：github.com/WhereIsHeroFrom/Code_Templates

---

---

六、分组背包相关题集整理

题目链接	难度	解析
洛谷 P1757 通天之分组背包	★★☆☆☆	【例题1】分组背包 / 最多1个
HDU 1712 ACboy needs your help	★★☆☆☆	分组背包 / 最多1个
HDU 3033 I love sneakers!	★★★☆☆	【例题2】分组背包 / 至少1个
PKU 1837 Balance	★★★☆☆	【例题3】分组背包 / 正好1个
HDU 4341 Gold miner	★★★☆☆	分组背包 / 最多1个
PKU 2392 Space Elevator	★★★☆☆	分组背包 / 最多1个 / 每组物品有自己的容量上限
HDU 3535 AreYouBusy	★★★☆☆	【例题4】混合背包 / 至少1个 / 最多1个 / 0/1背包
HDU 4345 Permutation	★★★☆☆	【例题5】置换群 + 算数基本定理 + 分组背包 / 最多1个
HDU 3092 Least common multiple	★★★☆☆	【例题6】算数基本定理 + 分组背包 / 最多1个
PKU 3590 The shuffle Problem	★★★★☆	置换群 + 算数基本定理 + 分组背包 / 最多1个
HDU 6125 Free from square	★★★★★	算数基本定理 + 状态压缩 + 分组背包 / 最多1个