Leetcode 287 - Find the Duplicate Number

题目：

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Example1：

Input：[1,3,4,2,2]
Output：2

Example2：

Input：[3,1,3,4,2]
Output：3
Note：

1. You must not modify the array (assume the array is read only).
2. You must use only constant, O(1) extra space.
3. Your runtime complexity should be less than O(n2).
4. There is only one duplicate number in the array, but it could be repeated more than once.

---

思路:

该问题可以简化为链表环的问题。设置两个指针分别为慢指针（slow）和快指针（fast）。快指针的速度是慢指针的两倍。如果链表中存在环的话，快指针和慢指针一定会相遇的。之后将快指针返回链表的起点，让它和慢指针的速率一样。则他们再度相遇的点的数据即是重复的数据。

这里有一个问题。为何第二次相遇的点的数据就是重复的数据。

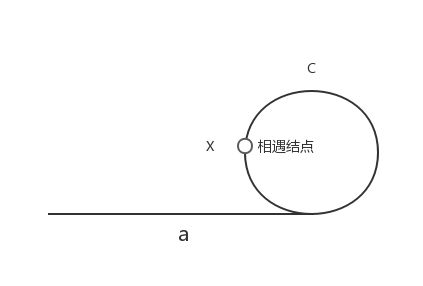
a：链表起点到环入口的距离。
c：圆环的周长。
x：相遇结点到圆环起点的距离。

快结点走过的距离i为a+n1*c+x，慢结点走过的距离为a+n2*c+x。由于快结点的速度为慢结点的两倍所以a+n1*c+x=2（a+n2*c+x）。最后得出a +x=c(n1-2n2)。n1代表快结点转过的圈数，n2代表慢结点转过的圈数。

由于圆圈中有一部分距离已经为x因此剩下的距离即链表起点到圆环入口的距离。因此当快结点从链表起点出发，慢结点以同样的速度从刚刚相遇的结点出发到它们会和，会和的结点一定是重复数字的结点。

---

代码：

public int findDuplicate(int[] nums) {
        int slow = 0;
        int fast = 0;
        do{
            slow = nums[slow];
            fast = nums[nums[fast]];
        }while(slow != fast);
        fast = 0;
        while(fast != slow){
            fast = nums[fast];
            slow = nums[slow];
        }
        return slow;
}