贝叶斯网络之父judea pearl说:我是AI社区的叛徒。
人工智能领域的先驱、贝叶斯网络之父 Judea Pearl 认为 AI 深陷于概率关联的泥潭,而忽视了因果。Pearl 认为研究者应该研究因果(Cause and Effect),这可能是实现真正智能的机器的可能路径。
一、贝叶斯定理
贝叶斯定理也称贝叶斯推理,一开始提出该理论是为了解决“逆向概率”的问题。
正向概率:工厂里有一台正常运行的机器,运行一段时间后生产了M个好灯泡,N个坏灯泡,问随便取一个灯泡,取到坏灯泡的概率是多大?
逆向概率:事先并不知道机器是否损坏,随机取好几次灯泡,根据灯泡的好坏,推断机器损坏的概率。
贝叶斯定理公式:
(1) 逆推案例
根据历史经验,已知完好的机器生产出好灯泡的概率为0.99,损坏的机器生产出好灯泡的概率为0.6。
现在突然检查到一个坏灯泡,请问机器正常运行的概率?检验员继续检查机器生产的下一个灯泡,发现依旧是坏灯泡,请问机器正常运行的概率?
这是一个典型的逆向推导问题,已知
现在已发现一个坏灯泡L=bad,求机器正常运行的概率
这里出现两个值P(M=workding)、P(M=broken)
先随便编一个,假设P(M=workding)=0.99,P(M=broken)=0.01
运算完以后输出两个值P(M=workding)=0.71、P(M=broken)=0.29
(2) 先验概率与边缘概率
这里需要提两个概念“先验概率”、“边缘概率”,有的地方把先验概率和边缘概率定义为同一个东西,都理解为“某个事情发生的概率”。我认为可以这样理解:
先验概率:是指根据以往经验和分析得到的概率。
边缘概率:推断得到的
上面的推导中,我们一开始随便设置P(M=workding)=0.99,P(M=broken)=0.01,这个值是根据历史经验中机器运行的表现判断的,我们把它称作先验概率。
已知检测到一个坏灯泡,经过贝叶斯计算以后得到P(M=workding)=0.71、P(M=broken)=0.29,这个值是计算得到的,和历史经验没直接关系,我们把它称为边缘概率。
(3) 贝叶斯推断
贝叶斯推断案例一
继续检查,发现第二个检查的灯泡仍是坏的
第一个灯泡是坏的,更新了机器正常运行的概率,此时输入的P(M=workding)=0.71、P(M=broken)=0.29
所以连续第二个还是检查到坏灯泡,大概率上机器是坏掉了。
贝叶斯推断案例二
著名的三门问题,现场有三扇关闭了的门,其中一扇的后面有辆跑车,而另外两扇门后面则各藏有一只山羊。一直C门后面是山羊,请问你选择的门后有概率是多少?
事件A代表你第一次选择的门后是跑车,B代表主持人翻开的门后是山羊,现在B已发生。
先验概率,根据历史经验有1/3的概率选中跑车,P{A}=1/3
P(B)主持人翻开的门后是山羊的概率,按照节目关心,主持人会打开山羊的门,P(B)=1
主持人一定选择山羊,事件B一定发生:P{B|A} = 1
所以不换的胜率是1/3,因此一定要换。
贝叶斯推断案例三
最经典的一个例子就是疾病检测,假设某种疾病在所有人群中的感染率是0.1%,医院现有的技术对于该疾病检测准确率为 99%。
如果从人群中随机抽一个人去检测,医院给出的检测结果为阳性,那么这个人实际得病的概率是多少?
先验概率:根据历史经验判断。P(患病)=0.001
如果已经患病,被检测出来的概率 P(检测为阳性|患病)=0.99
由于疾病的患病概率实在很小,导致该疾病哪怕检测出来为阳性,实际患病的概率依旧很小(四舍五入等于没可能患病,别担心)
于是,不死心又去检查了。
如果第二次检查为阳性
因为第一次为阳性修正了患病概率,此时P(患病)=0.09
如果已经患病,被检测出来的概率 P(检测为阳性|患病)=0.99
如果第二次检查为阴性
因为第一次为阳性修正了患病概率,此时P(患病)=0.09
如果已经患病,被误检的概率 P(检测为阴性|患病)=0.01
如果第二次检测为阴性,就完全可以放心了,复检结果大大提高了检测的可信度。
以上推论案例,都是贝叶斯算法解决“逆向概率”的问题。在实际生活中,贝叶斯推论应很广泛。
二、贝叶斯网络
有向图模型,也称为贝叶斯网(BayesianNetwork,BN),其网络结构使用有向无环图。
(1) 联合概率与边缘概率
首先梳理贝叶斯网络的两个重要概念及其计算。
联合概率定义:表示XXX个事件共同发生的概率。
边缘概率:某个事件发生的概率。
已知天空是多云的,没打开过洒水器,之前下过雨,所以早晨起来看见地面是湿的有多大的概率?
联合概率 可以理解为P(多云,没打开洒水器,下过雨,早上地湿)四件事一起发生的概率。
边缘概率 就是早上起来P(早上地湿)的概率。看上去好像很简答,但P(早上地湿)要考虑多种情况。
联合概率
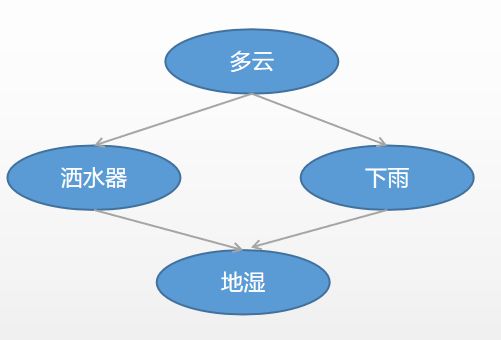
假如我们在照看花园,草地是湿的。我们想知道草地为什么是湿的。有两种
可能:之前下过雨或者我们忘记关掉洒水器。而且,我们可以观察天空。如果是多云天气,就有可能之前下过雨。但是,如果是多云天气,我们很有可能不会打开洒水器。
观察下图,每个结点旁边都有一个表格,表示T发生与F不发生的概率,我们把这个概率叫做条件概率。根据父节点的发生/不发生定义自身发生/不发生的概率。例如P(rain=F|cloudy=F)=0.8
左侧栏为这幅图可能发生的所有联合概率,例如不是多云,没有下雨,也没有打开洒水器,早上地也不湿这样的情况发生的概率为:P(Cloudy=0,Spring=0,Rain=0,Wet=0)=0.200
让我们来看看联合概率是怎么计算的。
由于图的特殊性,贝叶斯网络的联合概率公式为:
即该结点发生的条件概率之和夫结点有关系,不考虑没有连接关系的几点。
例如:
计算c=0,s=0,r=0,w=0同时发生的概率(联合概率)
计算c=0,s=0,r=0,w=1同时发生的概率(联合概率)
其他组合的联合概率参见上图左侧。
边缘概率
边缘概率 Marginal Probability 是某个事件发生的概率。
方法一
边缘概率是这样得到的:在联合概率表中把那个事件相关的概率求和。
例如求 就是把上面联合分布表中s=1的概率求和
方法二
边缘概率公式为:
所以s=1发生的概率为0.3
对于洒水器的打开与否,我们之前只知道如果不是阴天,有0.5的概率打开洒水器,如果是阴天只有0.1的概率打开洒水器。这个概率我们可以根据历史数据统计出来。
| C | P(S=F) | P(S=T) |
|---|---|---|
| F | 0.5 | 0.5 |
| T | 0.9 | 0.1 |
还记得我们上面将先验概率和边缘概率的差别,两者都是描述一个事前发生的概率,但边缘概率是需要推断得到。
(2) 贝叶斯网络
已知结点和结点之间的连接关系,同时还知道了子节点和父节点间的条件概率,此时我们就可以求联合概率和边缘概率了。联合概率解答了一串事情共同发生的可能,边缘概率解答了某个结点发生的概率(例如,早晨起来地是湿的概率)。
在实际应用中,求解联合概率和边缘概率倒是其次,如果结点很多,关联关系复杂些,困难的是条件概率的构建。以Wetgrass为例,有两个父结点,构建的条件概率表为行;如果有三个父节点,则条件概率表为行;如果有n个父节点,则条件概率表为行。
考虑计算机性能一般32个父结点,行的条件概率会超出内存限制导致无法计算。
| S | R | P(S=F) | P(S=T) |
|---|---|---|---|
| F | F | 1.0 | 0 |
| T | F | 0.1 | 0.9 |
| F | T | 0.1 | 0.9 |
| T | T | 0.01 | 0.99 |
参考资料
[1] 专访贝叶斯网络之父Judea Pearl:我是AI社区的叛徒https://baijiahao.baidu.com/s?id=1600692668193032477&wfr=spider&for=pc
[2] 《白板推导概率图》
https://www.bilibili.com/video/av33545406?from=search&seid=13894407203892398291
[3]什么是联合分布概率
https://wenku.baidu.com/view/7192db6d66ec102de2bd960590c69ec3d4bbdb76.html
[4] 贝叶斯算法及应用:https://www.bilibili.com/video/av39800693?from=search&seid=7055609900300366029
[5] 三门问题:http://baijiahao.baidu.com/s?id=1604863307926406800&wfr=spider&for=pc