详细介绍有关RACE数据集上经典的机器阅读理解模型如Co-Matching Model for Multi-choice, DCMN,DCMN+
A Co-Matching Model for Muti-choice Reading Comprehension
对于RACE这种多项选择式阅读理解数据集,不同于片段抽取式数据集,因为多项选择式是有三个句子成分的,(passage,question,choice)。以往的做法是用句子匹配的方式,比如把(question,choice)连在一起看成一个句子,然后与passage做匹配,如果这个这个choice是正确答案,那么匹配结果为1。或者先让passage和question做匹配,匹配出来一个向量,然后让这个向量和choice做匹配,计算出来一个分数,代表预测这个选项为正确答案的概率。然后重复其它三个选项,计算出来四个分数。
那么这些方法的缺点在于
- 如果把(question,choice)连在一起看成一个句子,然后与passage做匹配,那么问题和选项之间没有交互的信息,如论文中的表1所示的问题2,选项c中的He 和it 指代问题中的author 和island 所以问题和选项之间不能缺少交互。
- 如果把问题和passage先做匹配,计算结果然后再与选项匹配,那么不妥的地方在于,选项和问题应该是同等重要程度,仅仅让问题和passage做匹配可能没有意义。
论文中把question和choice看做是两个句子,让passage既和question做匹配也和choice做匹配,因此也叫co-matching。这样做之后那么passage中的每一个单词就同时关注到了question和choice。
按照论文中的公式符号来
H p , H q , H a H^p,H^q,H^a Hp,Hq,Ha就是经过循环神经网络后的上下文表示向量。这里面的 A A A表示的是一个choice。
注意力的计算方式多种多样,按照方向来讲可分为单向和双向,按照计算方式来讲可分为one-hop和multi-hop。multi-hop指的是当前时间步计算的注意力结果要流到下一个时间步。例如典型的机器翻译中的attention就是multi-hop,当前时间步decoder端的单词的隐藏状态和encoder端做attention,计算的attention结果要作为decoder端下一时间步单词输入的一部分。
而one-hop是指注意力只计算一次,比如论文中的公式(2),我们会发现直接拿 H q , H p H^q,H^p Hq,Hp做attention计算,其实计算的方式有多种,不一定非要像公式2那样。
计算的 G q G^q Gq形状是(batch_size,question_length,passage_length), G a G^a Ga形状是(batch_size,choice_length,passage_length)。
这两个就是attention weights, G q G^q Gq表示的是passage中每一个单词对question中每一个单词的注意力, G a G^a Ga表示的是passage中每一个单词对选项中每一个单词的注意力,然后分别对问题和选项加权求和(weighted sum)。得到 H ^ q , H ^ a \widehat{H}^q,\widehat{H}^a H q,H a,如论文公式(2)。
H ^ q , H ^ a \widehat{H}^q,\widehat{H}^a H q,H a的形状都是(batch_size,passage_length,dim)
其中 H ^ q \widehat{H}^q H q的意义代表的是对于passage_length中的每一个单词,我得到了一个新的特征向量长度是dim,而这个特征向量是我关注到了question中的每一个单词得到的。 H ^ a \widehat{H}^a H a的意义就是这个新的特征向量是我关注到了选项中的每一个单词得到的。
然后分别的,把 H ^ q \widehat{H}^q H q与 H p H^p Hp做element_wise减法和element_wise乘法,然后向量拼接,通过一个激活函数为RELU的全连接层得到 M q M^q Mq
, M a M^a Ma的计算方式同理。
至于为什么要这么做呢?首先 H ^ q \widehat{H}^q H q的含义解释过了,它是passage中每一个单词新得到的特征,这个特征是注意到了question得到的,所以它编码的是question方面的信息。而 H p H^p Hp是passage中每一个单词原来的上下文表示,它编码的是passage的信息。那么这种减法和乘法就可以将这两方面的信息进行比较,更好的构造出交互的特征,这比简单的将 H ^ q \widehat{H}^q H q和 H p H^p Hp直接向量拼接然后送入后面的层效果更好。
然后就是公式(3)把这两个向量拼接得到 C C C。
注意公式是这么写的,但看图1就可以看出,它是分句子的,那么我们现在得到的C.shape==(batch_size,passage_length,dim)。而passage_length是由多个sequence_length组成的,所以把C分开为N份,N代表passage是由几个句子构成的,于是乎得到 C 1 , C 2 , ⋯ , C N C_1,C_2,\cdots,C_N C1,C2,⋯,CN,看图
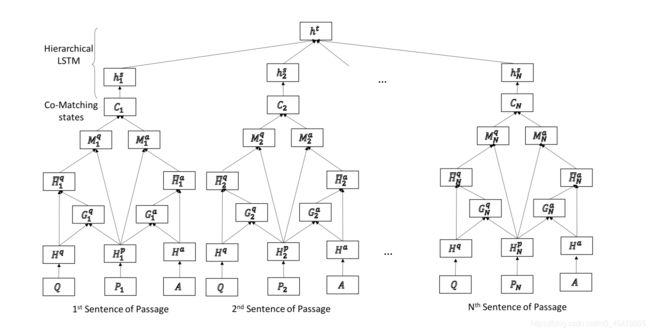
注意每一个 C i C_i Ci的shape是不一样的,因为每一个句子长度不一样,然后是公式(4)
对每一个 C i C_i Ci通过BiLSTM,BiLSTM的输出shape==(batch_size,sentence_i_length,dim),然后在句子长度这一维度做最大池化,自然得到的是固定长度的向量(batch_size,dim),一共会得到N个向量,N是passage中的句子个数。
然后是公式(5),把上面每一个向量连接,得到 H s H^s Hs,形状毫无疑问是(batch_size,N,dim)。好了讲到这里要说明的是 C i C_i Ci是word_level即单词级别的语义表示,把C_i通过BiLSTM再做最大池化后(也可以不做池化,取最后一个单词的隐藏状态也可以)得到的 h i s h_i^s his是sentence-level即句子级别的语义表示,
然后看公式(5),把每一个 h i s h_i^s his通过BiLSTM后再做maxpooling此时得到的 h t h^t ht就是document即文章层面的语义表示 h t h^t ht的shape==(batch_size,dim)
。
由于我们是四个选项,所以会得到四个 h t h^t ht,也就是 h 1 t , h 2 t , h 3 t , h 4 t h_1^t,h_2^t,h_3^t,h_4^t h1t,h2t,h3t,h4t。shape都是(batch_size,dim)。接下来就是输出层了
所谓的输出层就是一个全连接层,输出的维度是1,采用softmax函数,如公式6,显然损失函数是交叉商。在编程时,到了这步,具体的:
我们标签的形状是labels=(batch_size,4),它是one_hot形式的,比如第一个值是(0,1,0,0)那就表示batch_size个样本中的第一个样本的第二个选项是正确答案。
我们将得到的那四个 h t h^t ht通过同一个网络层,得到四个张量,每一个值都是(batch_size,1)形状的,然后将张量堆叠在一起就是(batch_size,4),这就是logits,预测的时候要的就是这个,argmax(logits)得到的值就是预测的选项。
那么损失函数自然也就是将logits与labels做交叉商:
loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits,labels))
以上就是这篇论文的总体思路。
接下来介绍DCMN
Dual Co-Matching Network for Multi-choice Reading Comprehension
开始挑毛病了:
- 上一篇论文中可以看到它只是做了问题对文章以及选项对文章这个方向做注意力,没有做文章对问题,文章对选项这个方向的注意力。这一点看上一篇论文的公式(2)。所以第一个毛病是不是双向的。
- 上一篇论文中可以看到它并没有在问题和选项之间做交互,这是第二个毛病。
正如上面提到的例子:He 和it 指代问题中的author 和island 所以问题和选项之间不能缺少交互。有趣的是这个例子是上一篇论文中指出的,而它却没有做问题与选项之间的注意力。
除了解决上面两个缺点外,DCMN这篇论文在融合 M M M的时候,我所说的 M M M就是上篇论文中的 C C C,如下图

,DCMN这篇论文中融合位置如下图

上一篇论文的融合只是简单的向量拼接,缺点是把所有的信息都融合在一起,
而我们知道有用的信息应该流向后面,没用的信息不应该让它通过,所以引入门控融合机制,具体的后面详解。
除了上述三点改进之外,这篇论文用的是BERT做编码器。
好了具体看模型:
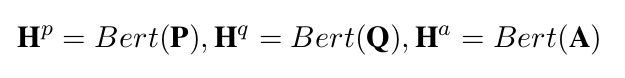
显然是把BERT的输出向量作为语义编码,这没什么好说的。
接下来是匹配层,为了简洁,论文中只给出了passage和choice之间如何计算,其它两个(passage,question)和(question,choice)同理。
看公式(1):
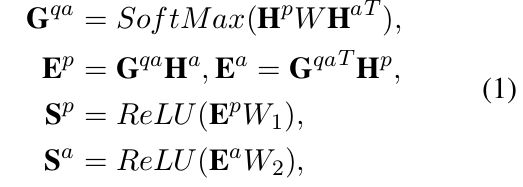
G q a G^{qa} Gqa其实应该是符号打错了,应该是 G p a G^{pa} Gpa,表示的是passage和choice之间的attention weights。注意力的计算方式就是简单的乘积。
然后用attention weights对相应的张量加权求和。 E p E^p Ep.shape==(batch_size,passage_length,dim), E a E^a Ea.shape==(batch_size,choice_length,dim)
然后分别通过通过带有RELU激活函数的一个全连接层得到 S p , S a S^p,S^a Sp,Sa。
S p , S a S^p,S^a Sp,Sa的形状与 E p , E a E^p,E^a Ep,Ea的形状一一对应。对于 S p S^p Sp或者 E p E^p Ep来说,每一行表示的是passage中某一个单词的新的特征向量,这个特征向量是关注到了选项后计算出来的。对于 S a S^a Sa或者 E a E^a Ea来说,这个新的特征向量是关注到了passage后得到的。
然后看公式(2)
首先在第一个维度上做最大池化,得到一个固定长度的向量, M p , M a M^p,M^a Mp,Ma。
此时做出来一个门控函数g,它用来决定 M p , M a M^p,M^a Mp,Ma具体哪些信息应该流向后面的层。这种门控的思想就是来源于LSTM的。
于是乎得到了 M p _ a M^{p\_a} Mp_a。形状是(batch_size,dim)。它的第i行表示的是,
对于当前batch_size中的第i个样本来说,我们有一个长度为dim的向量,这个向量既关注到了passage也关注到了choice。,而且还存储的都是有用的信息,你说厉不厉害。
那么相应的也可以得到 M p _ q , M q _ a M^{p\_q},M^{q\_a} Mp_q,Mq_a。
接下来就是输出层。
注意我们一共有四个选项,每一个选项都会计算出来上面三个向量
即:
c 1 = [ M p _ q , M p _ a 1 , M q _ a 1 ] c_1=[M^{p\_q},M^{p\_a_1},M^{q\_a_1}] c1=[Mp_q,Mp_a1,Mq_a1]
c 2 = [ M p _ q , M p _ a 2 , M q _ a 2 ] c_2=[M^{p\_q},M^{p\_a_2},M^{q\_a_2}] c2=[Mp_q,Mp_a2,Mq_a2]
c 3 = [ M p _ q , M p _ a 3 , M q _ a 3 ] c_3=[M^{p\_q},M^{p\_a_3},M^{q\_a_3}] c3=[Mp_q,Mp_a3,Mq_a3]
c 4 = [ M p _ q , M p _ a 4 , M q _ a 4 ] c_4=[M^{p\_q},M^{p\_a_4},M^{q\_a_4}] c4=[Mp_q,Mp_a4,Mq_a4]
每一个 c i c_i ci的shape都是(batch_size,3*dim)
注意论文中 V ∈ R l V\in R^l V∈Rl有误,应该是 V ∈ R 3 l V\in R^{3l} V∈R3l,这一点在后面的DCMN+中改过来了。
现在做的就是要把每一个 c i c_i ci通过一个输出维度是1的全连接层,而论文中的 V V V就是这个全连接层的权重参数。
这样我们就得到了四个output比如 o u t 1 , o u t 2 , o u t 3 , o u t 4 out_1,out_2,out_3,out_4 out1,out2,out3,out4
每一个out形状都是(batch_size,1)。
然后将张量堆叠起来形成output,它的shape==(batch_size,4),和标签做交叉商,具体的如上面那篇论文所述。
好了,DCMN论文大致就是这样
接下来就是DCMN+:
DCMN+: Dual Co-Matching Network for Multi-choice Reading Comprehension
这个DCMN+想要说明的一件事是:要想提高模型的精度,不一定非要在预训练上下功夫,比如XLNet,不是土豪的话根本做不了实验了。对于BERT这种预训练模型加上好的fine-tuning结果一样可以达到更高的效果。
直接看图
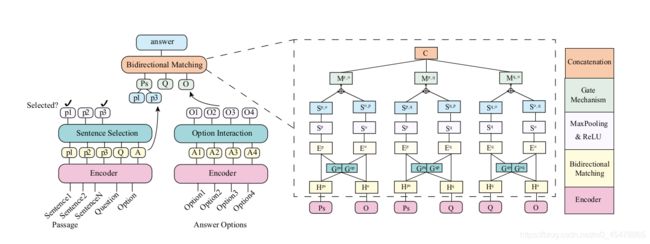
从图中我们可以看出,主要分为三部分,第一部分是sentence selection,第二部分是Option interaction,第三部分是matching,其中第三部分类似于上一篇DMCN。
这里一开始有个问题就是sentence selection这里的Option,我们说一共四个option,那么这个option应该是哪个option?
在option interaction这个模块里四个option是一起放进去的,然后交互,最后出来四个张量,此时每一个张量里面的特征是和其它三个选项交互后得到的,然后这四个张量的每一个都要和句子选择模块中选择出来的几个句子以及问题做matching,于是乎我觉得,在sentence selection这里的option应该是这样的:
首先我们可以看出答案交互模块和句子选择模块是独立的,所以我们可以先做答案交互模块,计算得到的四个张量分别代表一个选项,此时假如我拿第一个张量,那就代表我拿的是第一个选项,下面我将要对这个选项打分来判断它是不是答案,于是在句子选择模块中的option我觉得此时就应该是第一个option,利用第一个option去找出passage中的几个句子。其它的option同理,于是这样最后会得到四个分值,分别代表这四个选项的预测概率。
也就是说答案交互层会拿出一个张量给matching层,句子选择层会根据某一个选项选择出来几个句子给matching层,至于这几个句子是根据哪个选项选择出来的,要看答案交互层拿出来的张量代表的是第几个选项。
好了下面我们看模型:
我们先看答案交互层:
看公式5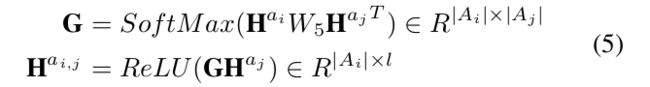
假如现在我们想要获得选项j对选项i的注意力,那么我们就要先拿选项i和选项j的隐藏状态做计算获得注意力权重矩阵G,它的形状就是
(batch_size,choice_i_length,choice_j_length),然后利用G对选项j做weigthed sum加权求和,得到 H a i , j H^{a_{i,j}} Hai,j,它的形状就是(batch_size,choice_i_length,dim)
对于第一个选项来说,它会获得三个张量,也就是和其它三个选项计算得到的。
即 H ^ a 1 = [ H a 1 , 2 , H a 1 , 3 , H a 1 , 4 ] \widehat{H}^{a_1}=[H^{a_{1,2}},H^{a_{1,3}},H^{a_{1,4}}] H a1=[Ha1,2,Ha1,3,Ha1,4],将这三个张量相连接得到的 H ^ a 1 \widehat{H}^{a_1} H a1的shape==(batch_size,choice_1_length,3*dim)
按照论文中的公式6,还要乘以 W 6 W_6 W6给它的维度变为dim。这是因为要利用门控单元的话必须保证输入的维度得要一致。
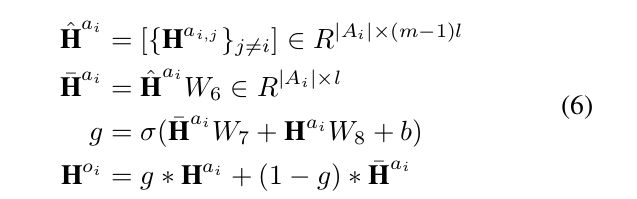
现在已经获得了 H ˉ a i \bar{H}^{a_i} Hˉai,它的shape和 H a i H^{a_i} Hai一样是(batch_size,choice_i_length,dim)。 H a i H^{a_i} Hai是BERT编码器的输出,所以 H a i H^{a_{i}} Hai的每一个值表示的是这个选项中的每一个单词的语义向量,也就是这个张量关注的是选项i本身的语义表征。而 H ˉ a i \bar{H}^{a_i} Hˉai是经过与其它三个选项交互后得到的语义表征(从公式5和公式6可以看出来),这个张量关注的是除了选项i外的其它三个选项的语义表征。
那么接下来常规的简单的做法是把这两个张量拼接送入后面的网络,但是正如上篇论文说的,这种做法不管信息的重要性,将所有得到的信息都送到后面,于是利用门控思想控制将重要的信息流向后面,不重要的阻断。
门控的做法就是公式6的后两个。
g a t e = σ ( H ˉ a i W 7 + H a i W 8 + b ) H o i = g ∗ H a i + ( 1 − g ) ∗ H ˉ a i gate=\sigma(\bar{H}^{a_i}W_7+H^{a_i}W_8+b) \\ H^{o_i}=g*H^{a_i}+(1-g)*\bar{H}^{a_i} gate=σ(HˉaiW7+HaiW8+b)Hoi=g∗Hai+(1−g)∗Hˉai
其实所谓门控都是类似的运算机制,可以参考LSTM那三个门的做法,比如忘记门 f = σ ( W i f x t + W h f h t − 1 + b f ) f=\sigma(W_{if}x_t+W_{hf}h_{t-1}+b_f) f=σ(Wifxt+Whfht−1+bf)。都是采用sigmoid函数,当sigmoid=0时,代表门关闭,因为你乘以的是0啊,所以什么信息都不会流到后面。sigmoid=1代表门完全打开,信息全都会流到后面。
话说回来,计算得到的 H o i H^{o_i} Hoi代表的就是选项i。
然后到了句子选择模块:
此时拿第i个选项去提取top K重要的句子,这个K是要预先指定的。
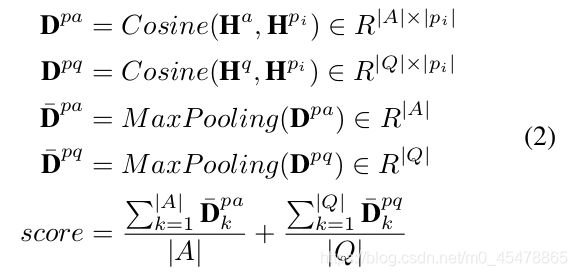
从公式2中可以看出 H a H^a Ha就是第i个选项的BERT输出张量。把passage分成多个句子,每一个句子都分别的和选项以及问题做余弦距离的计算。
具体的: 一篇passage有五个question记为question1,question2,question3,question4,question5。每一个question有四个choice,记为choice_1,choice_2,choice_3,choice_4。再假设这篇passage有10个sentence。那么一篇文章其实就是五个example,即(passage,question1,choice_1…choice_4)…(passage,question5,choice_1…choice_4),假如我们的batch_size就是5,也就是说以一篇文章为一个批次送入模型,那么batch[0]就是把question1的四个choice送入模型先做choice interaction,然后对于计算出来的四个张量tensor1,tensor2,tensor3,tensor4的每一个张量,选取相应的choice,比如tensor1,那么就选出来choice_1,再加上passage和question1送入sentence selection模块,此时把passage划分成十个sentence,每一个sentence都要按照公式2的计算步骤得到一个score,然后得出的10个score,选取top K,假设k=3,那么将选出来三个句子连接,再加上question1以及选项交互模块对应的张量tensor1送到matching层,计算出来的分数就是对choice_1的分数。其他的choice同理。
了解了上面的过程我们再来看具体的公式2:
首先 D p a D^{pa} Dpa的第一行表示的选项中的第一个单词和句子i的所有单词之间的相似度,那么第一行的最大值就是在句子i中挑选出来和选项的第一个单词最相近的那个单词。显然第二行的最大值就是在句子i中挑选出来和选项的第二个单词最相近的那个单词,于是乎:
D ˉ p a \bar{D}^{pa} Dˉpa表示的就是将句子i中与选项最相近的单词挑选出来
同理:
D ˉ p q \bar{D}^{pq} Dˉpq表示的就是将句子i中与问题最相近的单词挑选出来
从而对 D ˉ p a \bar{D}^{pa} Dˉpa表示的就是passage和choice之间的相似度, D ˉ p q \bar{D}^{pq} Dˉpq表示的就是passage和question之间的相似度。加和就代表句子i和选项以及问题之间的相似度
但是简单的相加不妥,原因是如果选项比较长或者问题比较长,那么显然加和的值越大,所以要取平均。这就是score。
Bidirectional Matching层和DCMN几乎是一样的,损失函数也是一样的,就不重复介绍了。