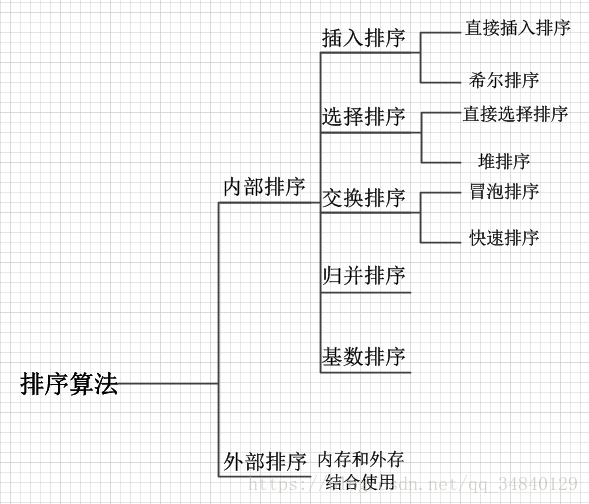
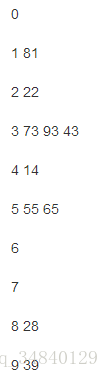学习笔记-简单的排序算法（Python实现）

1、直接插入排序

时间复杂度：O(n^2)

空间复杂度：O(1)

稳定性：稳定

插入排序就是将一个数据插入到已经排好序的序列中。

如图所示，插入元素是2，则用2依次与左边的元素比较，只要左边的元素大于2，就将左边的元素右移一位，直到2大于左边元素为止。

def insert_sort(lst):
    for i in range(1, len(lst)):
        x = lst[i]
        temp = i
        while temp > 0 and lst[temp-1] > x:
            lst[temp] = lst[temp-1] #只要左边元素大于右边元素，就将较大的元素交换到右边
            temp -= 1
        lst[temp] = x
    return lst

if __name__=="__main__":
    lst = [4,1,6,8,34,9,2,5]
    print(insert_sort(lst))

 

2、希尔排序

 

时间复杂度：与所选的增量序列有关

空间复杂度：O(1)

稳定性：不稳定

基本思想：取一个递减的增量序列{n/2，(n/2)/2，...，1}，首先取增量n/2，所有距离为n/2的倍数的记录放在同一个组中，在各组内进行直接插入排序；然后取第二个增量(n/2)/2，继续上述操作；直至所有的增量为1，即所有记录放在同一个组中进行直接插入排序为止。

该算法实质上是一种分组插入方法。进行一次比较可以跨过多个元素，可能消除多个元素交换。

def shell_sort(lists):
    length = len(lists)
    gap = length // 2
    while gap > 0:
        for i in range(0, gap):
            j = i + gap        #j是待插入元素位置
            while j < length:
                temp = j
                key = lists[temp]
                while temp > 0 and lists[temp-gap] > key: #利用直接插入排序将每个组中的元素排序
                    lists[temp] = lists[temp-gap]
                    temp -= gap
                lists[temp] = key
                j += gap #同一个小组中，再向已排序小组中插入j+gap位置的元素
        gap //= 2
    return lists

if __name__=="__main__":
    lst = [30,13,25,16,47,26,19,10]
    print(shell_sort(lst))

 

 

 

3、直接选择排序

时间复杂度：O(n^2)

空间复杂度为：O(1)

稳定性：不稳定

每次都顺序扫描出未排序序列中最小的元素，然后将其添加在已排序序列的末尾。

def select_sort(lst):
    for i in range(len(lst) - 1):  # 只需要比较len(lst)-1次，剩余的最后一个元素肯定是最大的
        min_position = i  # min_position记录最小元素的位置
        for j in range(i + 1, len(lst)):
            if lst[j] < lst[min_position]:  # 如果有更小的元素，则更新min_position
                min_position = j
        # if i != min_position: #有可能位置i已经是最小元素的位置，所以此时就不需要交换了
        #     lst[i], lst[min_position] = lst[min_position], lst[i]
        lst[i], lst[min_position] = lst[min_position], lst[i]
    return lst


if __name__ == "__main__":
    lst = [4, 1, 6, 8, 34, 9, 2, 5]
    print(select_sort(lst))

直接选择排序的实际排序效率低于插入排序。所以直接选择排序很少被实际应用。

将原来已排序序列的后一个元素交换到最小元素的位置，有可能出现两个相同的元素做交换，这说明算法不稳定。

延伸：

直接选择排序比较低效，是因为在做顺序扫描时，每次都需要从头做一次完整的比较，这个过程中做了很多重复的工作。要想克服这个缺点，就应该设法记录比较之后的获得的信息。利用树的结构来记录这种信息，由此出现了堆排序：图解堆排序。但是堆排序也可能出现两个相同元素被交换的情况。所以算法也具有不稳定性。堆排序的时间复杂度为O(nlog n)，空间复杂度是O(1)。

 

4、堆排序

时间复杂度为：O(nlog n)，

空间复杂度为：O(1)

稳定性：不稳定

当元素个数较少时，堆排序的大部分时间花在了堆的初始化和向下筛选上，当元素较多时，具有较好的效率。

具体原理和程序参见：点击打开链接

5、交换排序：冒泡排序

最坏的时间复杂度：O(n^2)

平均时间复杂度：O(n^2)

最好的时间复杂度：O(n)

空间复杂度：O(1)

一个未排序序列中，肯定存在逆序对（即前一个元素大于后一个元素），通过不断交换逆序对中两个元素的位置，最终将得到排序序列。

冒泡排序最坏的时间复杂度是O(n^2),平均时间复杂度也是O(n^2),最好情况下的时间复杂度是O(n)。其也是一种原位排序算法，空间复杂度是O(1)。是一种稳定的排序算法。

如果初始序列有序，则只需要扫描一次就结束了，时间复杂度是O(n)。

上图中的排序过程中，每一遍检查都可以将最大的元素交换到最后面。这就像水中的气泡浮起，也是这种算法名字的由来。

当序列中最小元素在序列的最后时，冒泡排序需要n-1遍扫描。在一般情况下，并不需要这么多次。只要在某次扫描中没有发现逆序对，则说明排序已经完成了。

def bubble_sort(lst):
    for i in range(len(lst)-1): #最多需要比较len(lst)-1次
        found = False #found变量初始为false，如果存在逆序对，则置为True，如果不存在，则为false，则会控制循环提前结束
        for j in range(1, len(lst)-i): #第一次需扫描n个元素，第二次需扫描n-1个元素，依此类推
            if lst[j-1] > lst[j]: #如果存在逆序对，则交换元素
                lst[j-1], lst[j] = lst[j], lst[j-1]
                found = True
        if not found:
            break
    return lst

if __name__=="__main__":
    lst = [30,13,25,16,47,26,19,10]
    print(bubble_sort(lst))

 

冒泡排序效率低于插入排序。一是因为反复交换相邻元素，累加起来代价较大；二是一些距离最终位置较远的元素会拖累整个算法。

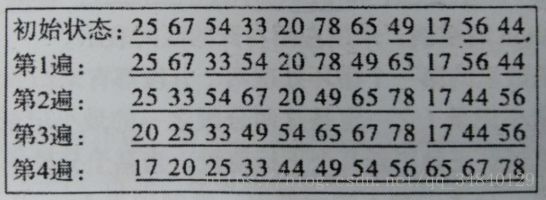
此外，还有一种交错起泡的算法，可以将小元素快速地移向左方。从左向右扫描一次，再从右向左扫描一次，交替进行。

只需要 4遍就可以完成以下的排序工作。

6、快速排序

时间复杂度：O(nlog n)

空间复杂度：O(log n)

稳定性：不稳定

快速排序算法在实践中是平均速度最快的算法之一。

基本思想是：从序列中选一个元素作为‘标准’，将序列中剩余的元素与这个标准一一比较，小于‘标准’的元素放在其左边，大于‘标准’的元素放在其右边；这样就将数据分割成了独立的两部分，然后在两个子序列中按照同样的方式递归地划分下去，直到整个数据变成有序序列。

算法实现：

取序列中第一个元素作为‘标准’，记为R。小于R的元素在其左边，大于R的元素在其右边，中间是尚未检查的元素。此外，下标i和j分别指向未检查元素序列的第一个位置和最后一个位置（i初始时指向整个序列的第一个元素）。然后交替进行如下操作：

(1)从位置j开始向左逐个比较当前元素与R的大小，直至找到第一个小于R的元素，将其存入位置i。然后i加1，指向下一个需要检查的元素。

(2)从位置i开始向右逐个比较当前元素与R的大小，直至找到第一个大于R的元素，将其存入位置j。

重复以上两步，直到i与j相等，此时将R存入i=j的这个位置，一次划分完成。

def quick_sort(lst):
    record = qsort_rec(lst, 0, len(lst)-1) #i和j分别初始化为序列的第0个和最后一个位置
    return record

def qsort_rec(lst, l, r):
    if l >= r:    #说明序列中没有元素或者只有一个元素
        return
    i, j = l, r
    standard = lst[i] #标准元素为序列中最左边的元素
    while i < j:      #终止时i=j
        while i < j and lst[j] >= standard: #从右向左找到第一个小于标准的元素
            j -= 1
        if i < j:      #将上面找到的元素放到位置i
            lst[i] = lst[j]
            i += 1
        while i < j and lst[i] <= standard: #从左向右找到第一个大于标准的元素
            i += 1
        if i < j:      #将上面找到的元素放到位置j
            lst[j] = lst[i]
            j -= 1
    lst[i] = standard
    qsort_rec(lst, l, i-1)
    qsort_rec(lst, i+1, r)
    return lst


if __name__=="__main__":
    lst = [30,13,25,16,47,26,19,10]
    print(quick_sort(lst))

 

 

如果每次划分都能将序列分成两个基本相等的子序列，那么整个序列将被分为大约log n层；在其中一层中，元素的比较次数不会超过序列的长度n，所以快速排序的平均时间复杂度是O(nlog n)。

 

 

但是，如果每层划分得到的两个子序列中总有一个为空，另一个子序列中的元素个数只比本层划分前少一个，这样需要分为n-1层，每层的比较次数从n-1逐层减少到1,。此时是快速排序最坏的时间复杂度O(n^2)。

其空间复杂度最坏时是O(n)，但是可以通过不同的实现方式，提升至O(log n)。

 

7、归并排序

时间复杂度：O(nlog n)

空间复杂度：O(n)

稳定性：稳定

基本过程：

• 首先，将待排序序列中的n个元素看作n个有序子序列，每个子序列长度为1。
• 然后，将当前序列中的有序子序列两两归并，完成一遍后整个序列中的已排序序列个数减半，每个子序列长度翻倍。
• 对长度翻倍后的子序列继续两两归并，最后将得到一个长度为n的有序序列。

归并排序适合处理存储在外存中的大量数据。

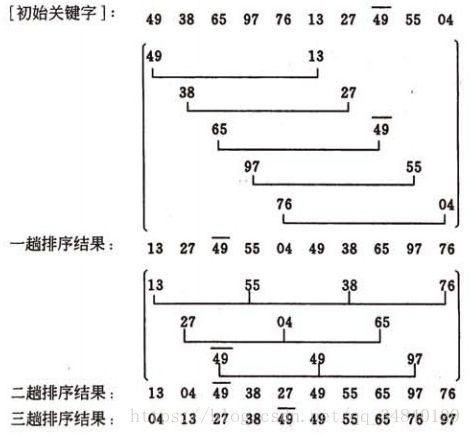
下图是一个例子：第一遍将序列归并为一组长度为2的有序序列，最后的元素44没有归并对象，原样留到下一步；第二遍归并出3个长度为4的有序序列；第三遍只能归并出一个长度为8的有序序列，剩余的3个元素原样留到下一步；最后一步便已经得到了排序序列。

 

# 实现一对有序序列的归并操作，将归并的结果存入另一个顺序表的相同位置。
def merge(lfrom, lto, low, mid, high):
    i, j, k = low, mid, low
    while i < mid and j < high:  # 每次都将两个子序列中最小的元素加入到lto中，但是总是会有某个序列的后面会剩下几个元素，需要下面的两个循环再将这些元素加到lto中
        if lfrom[i] <= lfrom[j]:
            lto[k] = lfrom[i]
            i += 1
        else:
            lto[k] = lfrom[j]
            j += 1
        k += 1

    while i < mid:  # 将第一个子序列的剩余元素加入到lto中
        lto[k] = lfrom[i]
        i += 1
        k += 1

    while j < high:  # 将第二个子序列的剩余元素加入到lto中
        lto[k] = lfrom[j]
        j += 1
        k += 1
    return lto


# 其中的某一遍归并操作，将表中的所有元素进行一遍归并
def merge_pass(lfrom, lto, list_len, sub_len):  # list_len为整个序列的长度，sub_len为子序列的长度
    i = 0
    while i + 2 * sub_len <= list_len:  # 处理序列中长度为sub_len的两个子序列
        merge(lfrom, lto, i, i + sub_len, i + 2 * sub_len)
        i += 2 * sub_len
    if i + sub_len < list_len:  # 此时剩下两个子序列，但只有第一个子序列的长度满足sub_len
        merge(lfrom, lto, i, i + sub_len, list_len)
    else:  # 否则，此时只剩下一个子序列，直接将这个子序列添加在lto后面
        for j in range(i, list_len):
            lto[j] = lfrom[j]


# 主函数，分配不同长度的sub_len，调用归并函数
def merge_sort(lst):
    sub_len, list_len = 1, len(lst)
    temp_lst = [None] * list_len
    while sub_len < list_len:  # 不断将sub_len的长度翻倍
        merge_pass(lst, temp_lst, list_len, sub_len)
        sub_len *= 2
        merge_pass(temp_lst, lst, list_len, sub_len)
        sub_len *= 2


if __name__ == "__main__":
    lst = [30, 13, 25, 16, 47, 26, 19]
    merge_sort(lst)
    print(lst)

8、基数排序

 

时间复杂度：O(d*(n+r))

空间复杂度：O(n+r)

稳定性：稳定

d为位数，r为基数，n为数组中元素的个数。

基数排序不需要将元素相互比较，只需要将元素分类即可。如果对效率有所要求，而不太关心空间的使用时，可以考虑使用。

下面以最低位优先法（LSD）为例：

原数组为：[73,22,93,43,55,14,28,65,39,81]

首先根据个位的数值，将元素分配到0~9的桶中：

然后将这些元素重新汇总起来：

[81,22,73,93,43,14,55,65,28,39]

在根据十位的数值来分配：

然后再将这些元素汇总起来：

[14,22,28,39,43,55,65,73,81,93]

此时的元素已经被排序完毕。

LSD适用于位数少的数列，如果位数多，则使用最高位优先法（MSD）。

MSD是从最高位开始进行分配，分配之后不马上汇总为一个数组，而是在每个桶中再建立子桶，将每个子桶中的元素按照下一数位的值分配到子桶中，在进行完最低数位的分配后，再汇总回一个数组中。

import math
def radix_sort(lists, radix=10):
    k = int(math.ceil(math.log(max(lists), radix)))
    bucket = [[] for i in range(radix)]
    for i in range(1, k+1):
        for j in lists:
            bucket[j//(radix**(i-1)) % (radix**i)].append(j)
        del lists[:]
        for z in bucket:
            lists += z
            del z[:]
    return lists

if __name__=="__main__":
    lst = [30,13,25,16,47,26,19,10]
    print(radix_sort(lst))

 

排序方法	最坏情况	平均情况	最好情况	空间复杂度	稳定性
直接插入排序					稳定
希尔排序					不稳定
直接选择排序					不稳定
堆排序					不稳定
冒泡排序					稳定
快速排序					不稳定
归并排序					稳定
基数排序					稳定

注：d为位数，r为基数，n为数组中元素的个数。

1、直接插入排序：对于一个无序的序列，需要将元素从第一位挨个取出，将其当做新元素插入到有序序列中；每个元素在插入到有序序列中时，需要从后向前与元素挨个比较。这里两个操作都需要遍历原序列，所以其时间复杂度最坏和平均时都是，当原来序列有序时，最好的时间复杂度是。

2、希尔排序的分析是一个复杂问题，与其所取的增量函数有关，其中涉及到数学上一些未解决的问题。一般认为在之间，较快的实现可以到。

3、直接选择排序：每次都需要顺序扫描出未排序序列中最小的元素，然后将其添加在已排序序列的末尾。其中需要遍历每个位置；在确定每个位置上的元素时，又需要从未排序序列中挨个比较出最小的一个元素。所以其时间复杂度都是。

4、堆排序：构建堆的时间是。交换堆顶与末尾元素，这个过程需要执行n次；堆顶元素下移的距离不会超过log n，所以重建堆的时间是。

5、冒泡排序：需要遍历n-1遍元素，第一遍遍历n个元素，第二遍遍历n-1个元素，......，依此类推，所以其时间复杂度为。当序列有序时，需要时间即可。

6、快速排序：最好的情况是每次取到的元素都刚好平分整个数组，这样便划分为了log n层，每层元素的比较次数不超过序列的长度。所以时间复杂度为。最坏的情况就是每次取到的元素都是数组中最大或者最小的（正序或者逆序排列），每次划分只得到比上一次少一个元素的子序列，此时需要时间。当每一次都平分数组时，其空间复杂度为；最坏情况时，空间复杂度为。

7、归并排序：完成整个排序的归并遍数不会超过log n + 1，在每遍归并中需要做的比较次数不会超过n，所以总的时间为。算法中需要用到一个与原数组同样大小的临时数组，所以其空间复杂度为。归并排序很消耗空间，一般内部排序不用，外部排序时才考虑使用。

8、基数排序：将元素分配到每个桶中的时间复杂度为，将元素再汇总起来的时间复杂度为，分配和汇总共需要d次，所以总的时间复杂度为。将元素进行‘装桶’操作时，都需要n+r个临时空间，所以空间复杂度为。