R语言时间序列分析-根据aic值选择arima模型

在上一篇中，探讨了R语言时间序列分析常用步骤，如何比对AIC值判断最优模型？代码和解释如下：

#WWWusage是datasets包自带的每分钟通过服务器连接到因特网的用户数的长度为100的时间序列数据

require(graphics) #画图判断平稳性，调用plot和par函数
win.graph(); plot(WWWusage) #明显带趋势，需要差分

work <- diff(WWWusage,1,1) #对其进行1阶差分，滞后期数lag为1
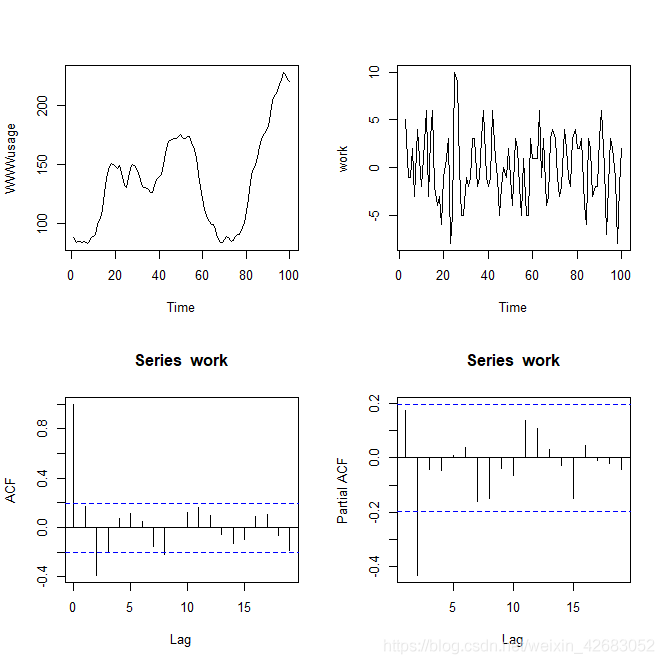
win.graph(); par(mfrow = c(2, 2)); plot(WWWusage); plot(work) 
acf(work); pacf(work)
tseries::adf.test(work)
#1阶差分后似乎变平缓了，但实际上是不平稳的，
#acf(work)和pacf(work)结果也能看出序列还未平稳。

work <- diff(WWWusage,1,2)
win.graph(); plot(WWWusage); plot(work); acf(work); pacf(work)
tseries::adf.test(work)
#根据tseries函数包的adf.test(work)进行单位根检验可知，2阶差分后序列才真正平稳了。

#创建一个6×6的矩阵，内容为NULL，行列名为p = 0:5, q = 0:5
aics <- matrix(, 6, 6, dimnames = list(p = 0:5, q = 0:5)) 

#使用arima函数，通过循环，将AIC值填入矩阵
require(stats) #调用arima函数

for(q in 1:5) #偏自相关系数q取值分别为1到5
  aics[1, 1+q] <- arima(WWWusage, c(0, 2, q), # q取值分别为1到5，结果放到矩阵的第一行2到6列
     optim.control = list(maxit = 500))$aic #将AIC值提取出来放在矩阵中

#optim.control是arima的优化参数，暂不讨论（我也不会，请读者指教）

for(p in 1:5) #自相关系数p取值分别为1到5
  for(q in 0:5) #偏自相关系数q取值分别为0到5
aics[1+p, 1+q] <- arima(WWWusage, c(p, 2, q), #当p=1时，结果放入第二行的1到6列，一直到第六行
#结果放到矩阵的第1+p行1到6列，即aics[2,1];aics[2,2];...;aisc[2,6];aics[3,1];...;aics[3,6];...;aics[6,1];...;aics[6,6]
       )$aic #将AIC值提取出来放在矩阵中

round(aics - min(aics, na.rm = TRUE), 2)
#min(aics, na.rm = TRUE) 找到aics矩阵中除了缺失值以外最小的元素
#aics - min(aics, na.rm = TRUE) 矩阵每个元素与最小值的差，发现0出现在第六行第6列，此时p=5,q=5
#round(aics - min(aics, na.rm = TRUE), 2) 四舍五入保留2位小数点

---

参考文献：R自带文档，我把内容改了一下，整成了2阶差分，然后再代入aic值计算

https://blog.csdn.net/weixin_42683052/article/details/116716505

---

更新：

通过对比，我们发现：

> arima(WWWusage,order=c(5,2,5))$aic
[1] 509.8135

> arima(WWWusage,order=c(2,2,0))$aic
[1] 511.4645

> arima(WWWusage,order=c(2,2,2))$aic
[1] 515.1303

表明arima(5,2,5)的模型最优，而arima(2,2,0)其次。

自相关图和偏自相关图的建议是arima(2,2,2)，但实际效果却不如arima(5,2,5)