【其他】结构技术优化算法--蚁群算法（ant colony optimization）

目录

 

1 遗传基因算法

2 模拟退火算法

2.1爬山算法

2.2随机概率优化

3 群体智能算法

3.1蚁群算法

3.2粒子群算法

4总结

---

1 遗传基因算法

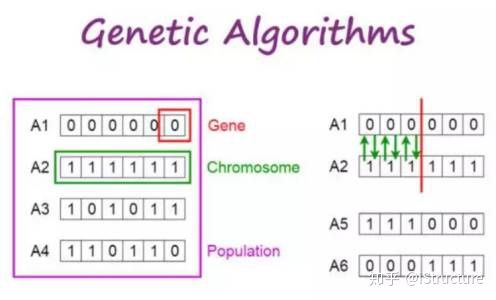
遗传算法（Genetic Algorithms，GA）由J.Holland教授（美国）1975年首先提出，是一种灵感源于达尔文自然进化理论的启发式搜索算法。该算法反映了自然选择的过程，即最适者被选定繁殖，并产生下一代。

运算过程为初始化→个体评价→选择运算→交叉运算→变异运算→终止条件判断，运算过程就如物竞天择、适者生存，只有被选择的个体才会把自己的基因传下去。下面就用一个有趣的例子，帮助大家理解。

我想让机器人小i画出我的梦中情人（最优解）。小i当然不知道我梦中情人长啥样。小i的内心是奔溃的，只能一张张试。先画一张，问我像不像？我说不像，小i就重新画一张，直到我觉得像。

然而小i又不会画画，只会填格子。于是小i准备了一张1000×1000的格子纸，每个格子可以填黑色或者白色。那么总共有21000000种画法。如果我能坚持到宇宙毁灭，那可以每张都看，然后找到那个最像的，显然我和我的梦中情人都坚持不到。

于是我只允许小i画10万张，画不出来我就砸了它。小i很紧张，开始想办法，终于想到了遗传算法。

第一轮，小i随机画了1万张（初始种群）。这1万张里面，各种乱七八糟，有像星空的，像猪的，像石头的，等等。然后小i让我挑最像的（个体评价）。我强忍怒火，挑出来一堆猪、猴、狗，好歹是哺乳动物（选择运算）。

 

小i拿着我挑的“猪猴狗们”，如获至宝，开始第二轮，将这些画各种交叉变异一下。比如把一幅画的耳朵跟另一幅的鼻子换一下（交叉运算），或者再随机改个眼睛（变异运算）。然后又生成了1万张图让我挑。我挑出来一堆猴子猩猩，好歹是灵长类动物。

如此反复好多轮后，挑出来的开始像人了，虽然有男人、女人。慢慢地，开始有美女了。再慢慢地，就越来越像了。在画了10万张图后，终于找到一张还不错的。虽然可能不是梦中情人（精确解），但也很像了（次优解）。

这就是遗传算法。

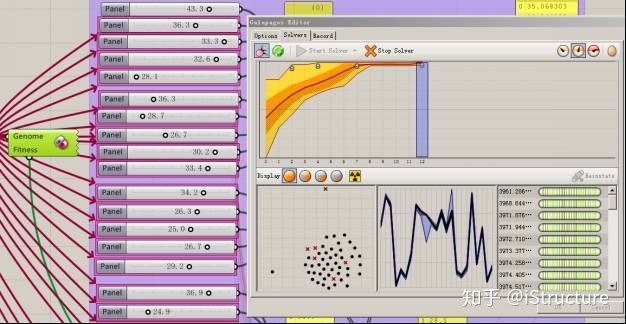
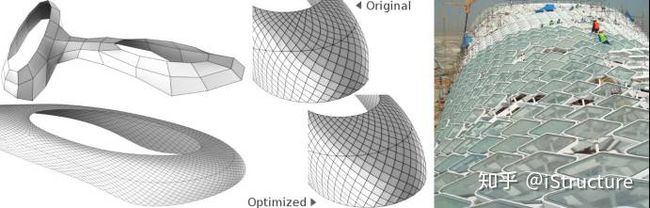
虽然我们已经知道了遗传基因算法的计算过程，但真正使用它，需要大量的编程。因此，对于普通结构设计人员，应用智能优化算法解决实际设计问题存在很大的难度。Grasshopper中开发了相应的优化算法模块，工程师可以利用这个模块便利的解决复杂问题，例如建筑设计中结构优化、幕墙优化等。

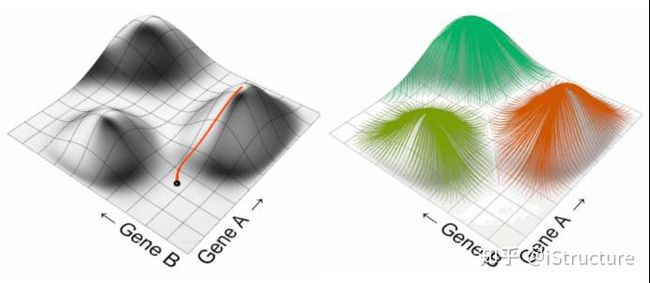
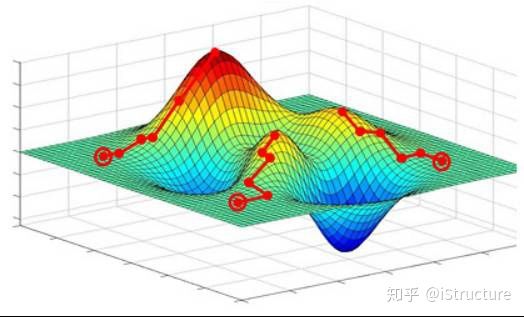
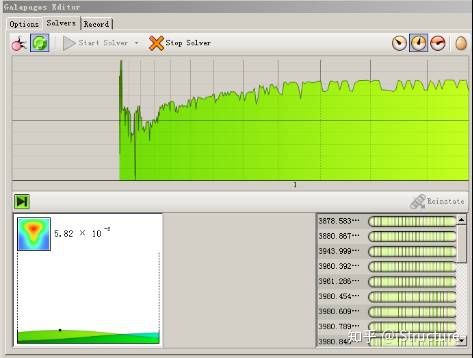
下面是一个二维运算的简单例子，介绍Grasshopper优化模块的原理。下图为一个山脉模型，这个模型包含了两个变量（近似看为X、Y坐标），他们可以同时变化。我们需要找出最高山峰处所对应的坐标值。

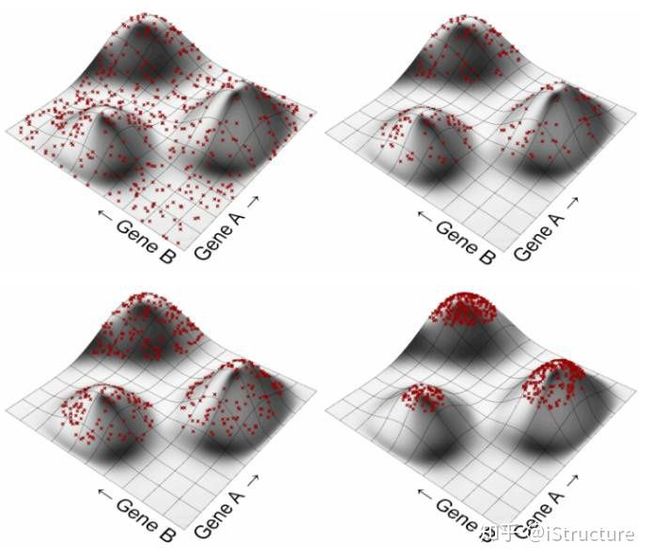
在一开始，电脑随即洒出一大堆随机点，我们假定为100个。随后选出位置较高的50个点，并在其周围再随即布置100个点，可以知道这100个点相对于他们上一代，更加靠近山峰。后面不断重复上一步，直到找到最顶峰的点。以上以二维山峰优化为例，计算机当然不止能运算二维变量，当我们初始变量不断增加时，也能得出最优解。当然，所需时间也更长。

2 模拟退火算法

2.1爬山算法

介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解中选择一个最优解作为当前解，直到达到一个局部最优解。

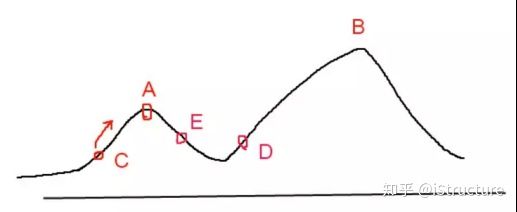
爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如下图所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。

这就是简单的爬山算法思想。

2.2随机概率优化

爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是找到更优的B点。

关于爬山算法与模拟退火，有一个有趣的比喻：

爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。

模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

同样，Grasshopper也提供了相应模块进行模拟退火算法。在实际应用中，推荐先采用遗传算法进行优化筛选，再结合类模拟退火算法可以提高了局部寻优的能力，采取分层优化的思想，提高运算效率。

3 群体智能算法

群体智能算法主要模拟了昆虫、兽群、鸟群和鱼群的群集行为，这些群体按照一种合作的方式寻找食物，群体中的每个成员通过学习它自身的经验和其他成员的经验来不断地改变搜索的方向。群体智能优化算法的突出特点就是利用了种群的群体智慧进行协同搜索，从而在解空间内找到最优解。

常见的群体智能算法有蚁群算法（Ant Colony Optimization，简称ACO）[1992年提出]；粒子群优化算法（Particle Swarm Optimization，简称PSO）[1995年提出]。下面小i简要介绍一下这两种算法。

3.1蚁群算法

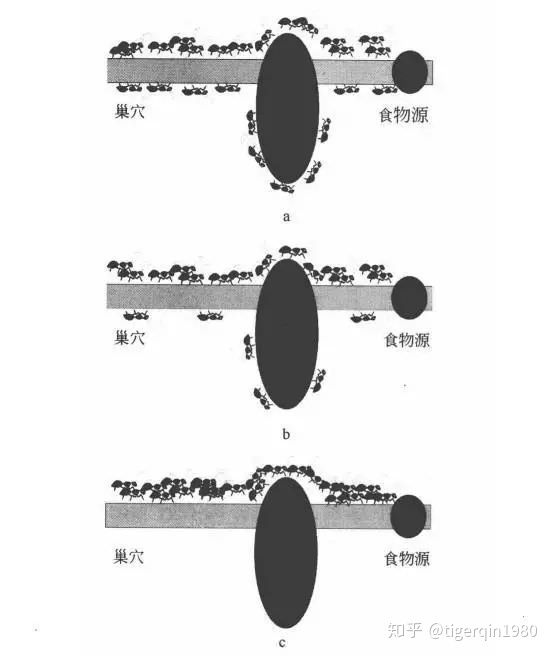
蚁群算法由Marco Dorigo于1992年提出，其灵感来源于蚂蚁觅食行为，无论食物和蚁穴之间的关系如何，蚂蚁总能找到两者之间的最短路径。研究表明，蚂蚁在爬过的路上会留下一种称为信息素(pheromone)的挥发性的物质，它提供了蚂蚁之间相互交流的途径。

蚂蚁在行进过程中遵循一种概率选路方式，如果路径没有其它蚂蚁留下的信息素，它完全按照随机方式选路，否则选择该路径的概率与信息素的强度成正比。一段时间以后，选择某一路径的蚂蚁越多，留下信息素的强度就越大，蚂蚁就是通过这种方法来选择最短路径的。

蚁群算法是一种本质上并行的算法。每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信，它在问题空间的多点同时进行独立搜索，不仅增加了算法的可靠性，也使得算法具有较强的全局搜索能力。

蚁群算法的基本思想:

 

蚁群算法的基本原理:
1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

蚂蚁在运动过程中，会留下一种称为信息素的东西，并且会随着移动的距离，播散的信息素越来越少，所以往往在家或者食物的周围，信息素的浓度是最强的，而蚂蚁自身会根据信息素去选择方向，当然信息素越浓，被选择的概率也就越大，并且信息素本身具有一定的挥发作用。 蚂蚁的运动过程可以简单归纳如下：

1. 当周围没有信息素指引时，蚂蚁的运动具有一定的惯性，并有一定的概率选择其他方向
2. 当周围有信息素的指引时，按照信息素的浓度强度概率性的选择运动方向
3. 找食物时，蚂蚁留下家相关的A信息素，找家时，蚂蚁留下食物相关的B信息素，并随着移动距离的增加，洒播的信息素越来越少
4. 随着时间推移，信息素会自行挥发

蚁群算法基本流程

 

一个简单的例子，如果现在有两条通往食物的路径，一条较长路径A,一条较短路径B,虽然刚开始A,B路径上都有蚂蚁，又因为B比A短，蚂蚁通过B花费的时间较短，随着时间的推移和信息素的挥发，逐渐的B上的信息素浓度会强于A，这时候因为B的浓度比A强，越来越多多蚂蚁会选择B，而这时候B上的浓度只会越来越强。如果蚂蚁一开始只在A上呢，注意蚂蚁的移动具有一定小概率的随机性，所以当一部分蚂蚁找到B时，随着时间的推移，蚂蚁会收敛到B上，从而可以跳出局部最优。

蚁群算法中主要参数的选择:

蚁群算法中主要参数的理想选择如下:

上面的描述可能不是很形象，现在我们来模拟做个小实验，实验地址Demo，源码已放在 Github

简单蚁群实验环境：

• 满足上面4点基本规则,信息素散播规则按照屏幕斜线距离/蚂蚁移动距离，移动距离在找到食物或者家清0(言外之意式，蚂蚁最多能够移动斜线这么远的距离，这个公式比较简单)
• 超过一定的移动步数未找到食物或窝的蚂蚁进行重置
• 选择方向的计算公式采用单元格浓度/8个方向单元格浓度总和,用轮盘赌进行概率选择
• 信息素在每次迭代时，进行统一挥发一个常量值

现在我们来看看蚂蚁是否能够找到最近的食物。

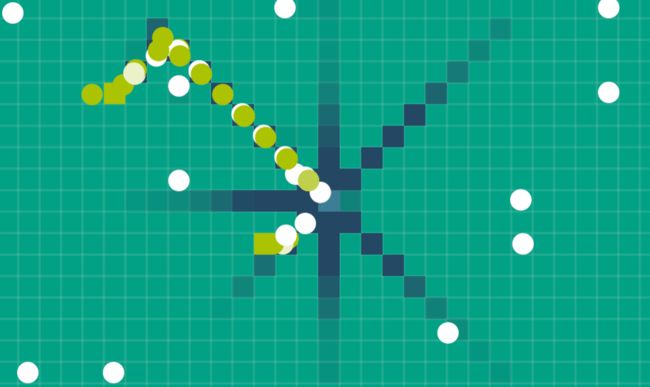
1.首先我们放置一个较远的食物A，图中的绿色为食物，白色为蚂蚁，暗蓝色为家相关的信息素，颜色深浅代表浓度。

注意：我们上面采用的信息素洒播规则，会让家相关的信息素浓度围绕着家呈梯形分布，这样蚂蚁在回家时，能够根据浓度找到家，食物相关信息素也一样。感兴趣的朋友可以在源码里修改信息素显示参数，显示食物相关的信息素分布图。

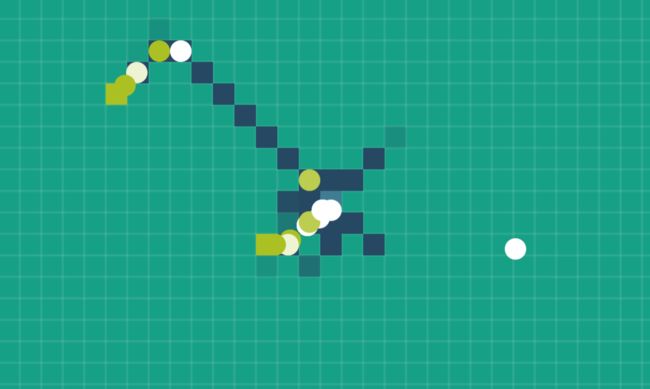
2.过一会儿，我们发现蚂蚁都聚集在这条路径上，然后我们放一个离得很近的食物B

3.最后我们会发现这条路径上的蚂蚁越来越多，再过一会儿，A路径上基本没有什么蚂蚁了。

你有可能问，那障碍是干嘛用的，我当时只是想干一件小时候经常干的事情，如

1.一群蚂蚁找到了食物

2.我拦住了他们的去路

3.最后他们还是找到了食物，坏笑

如果你亲自动手做实验，你会发现，当蚂蚁在一条路径上觅食很久时，你再放置一个近的食物基本没啥效果，你也可以理解为当一只蚂蚁找到一条路径时，过了很久的时间，大多数蚂蚁都选择了这条路径，就在这时候，突然有一只蚂蚁找到了较近的食物，但因为时间过得太久，两条路径上浓度相差太大（浓度越大，被选择的概率就越大），整个系统基本已经停滞了，陷入了局部最优。所以简单的蚂蚁系统是存在一些问题的，如：

1. 搜索到一定程度，会出现停滞状态，陷入局部最优的情况
2. 盲目的随机搜索，搜索时间较长

而影响蚂蚁是否能够找到好的最优解，依赖这几个关键因素：

1. 信息素怎么洒播（比如维持在一个特地范围的值等）
2. 信息素怎么挥发（除了全局挥发，可以让蚂蚁自身进行局部挥发等手段）
3. 通过怎样的方式让蚂蚁选择运动方向，减少盲目性和不必要性（给蚂蚁一点点智能和经验）
4. 给蚂蚁和环境一定的记忆能力能够帮助减少搜索空间

实际实验中发现，当蚂蚁在一条路径上觅食很久时，放置一个近的食物基本没有效果，这可以理解为当一只蚂蚁找到一条路径时，在经过很长时间后大多数蚂蚁都选择了这条路径，这时，突然有一只蚂蚁找到了较近的食物，但因为时间过得太久，两条路径上浓度相差太大（浓度越大，被选择的概率就越大），整个系统基本已经停滞了，陷入了局部最优。所以简单的蚂蚁系统是存在一些问题的，如： 搜索到一定程度，会出现停滞状态，陷入局部最优的情况 ↓ ↓ ↓

 

如果大家对蚁群算法 及 文中所叙内容 还有疑问或想要交流心得建议，欢迎在推文下留言沟通！

如果你感兴趣，可以去看看诸如最大最小蚁群算法、排序蚁群算法、基于遗传算法的蚁群算法等一系列在基本蚁群系统上的优化和改进，他们对于信息素的使用、蚂蚁方向选择等都有一套成熟的数学模型和经验优化参数。

人工蚁群与真实蚁群对比:

国内外，对于离散域蚁群算法的改进研究成果很多，例如自适应蚁群算法、基于信息素扩散的蚁群算法等，这里仅介绍离散域优化问题的自适应蚁群算法。

自适应蚁群算法：对蚁群算法的状态转移概率、信息素挥发因子、信息量等因素采用自适应调节策略为一种基本改进思路的蚁群算法。

自适应蚁群算法中两个最经典的方法：蚁群系统(AntColony System, ACS)和最大-最小蚁群系统(MAX-MINAnt System, MMAS)。

蚁群系统对基本蚁群算法改进:

①蚂蚁的状态转移规则不同；

②全局更新规则不同；

③新增了对各条路径信息量调整的局部更新规则

Code

先放上一波严肃的伪代码分析：

#include
using namespace std;
// const
const int INF = 0x3f3f3f3f;
#define sqr(x) ((x)*(x))
#define eps 1e-8
//variables
string file_name;
int type;// type == 1 全矩阵, type == 2 二维欧拉距离 
int N;//城市数量 
double **dis;//城市间距离 
double **pheromone;//信息素 
double **herustic;//启发式值 
double **info;// info = pheromone ^ delta * herustic ^ beta 
double pheromone_0;//pheromone初始值，这里是1 / (avg * N)其中avg为图网中所有边边权的平均数。 
int m;//种群数量
int delta, beta;//参数  
double alpha;
int *r1, *s, *r;//agent k的出发城市，下一个点，当前点。 
int MAX, iteration;//最大迭代次数，迭代计数变量 
set empty, *J;
struct vertex{
                     double x, y;// 城市坐标 
                     int id;// 城市编号 
                     int input(FILE *fp){
                     return fscanf(fp, "%d %lf %lf", &id,                          &x, &y);
}
}*node;

typedef pair pair_int;
struct Tour{//路径 
       vector path;//path[i]，存储一                     条边(r,s) 
      double L;
      void clean(){
              L = INF;
              path.clear();
              path.shrink_to_fit();
       }//清空 
      void calc(){
              L = 0;
              int sz = path.size();
              for (int i = 0; i < sz; i ++){
              L += dis[path[i].first][path[i].second]; 
              }
        }//计算长度 
      void push_back(int x, int y){
              path.push_back(make_pair(x, y));
        }
      int size(){
              return (int)path.size();
        }
      int r(int i){
              return path[i].first;
        }
      int s(int i){
              return path[i].second;
        }
      void print(FILE *fp){
              int sz = path.size();
              for (int i = 0; i < sz; i ++){
              fprintf(fp, "%d->", path[i].first + 1);
        }
              fprintf(fp, "%d\n", path[sz - 1].second +                    1);
        }
      bool operator <(const Tour &a)const{
               return L < a.L;
        }//重载 
} *tour, best_so_far;

double EUC_2D(const vertex &a, const vertex &b){
      return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
} 

void io(){//输入
      printf("input file_name and data type\n");
      cin >> file_name >> type;
      FILE *fp = fopen(file_name.c_str(), "r");
      fscanf(fp, "%d", &N);
      node = new vertex[N + 5];
      dis = new double*[N + 5];
      double tmp = 0;
      int cnt = 0;
      if (type == 1){
               for (int i = 0; i < N; i ++){
                    dis[i] = new double[N];
                    for (int j = 0; j < N; j ++){
                          fscanf(fp, "%lf", &dis[i][j]);
                          tmp += i != j ? dis[i][j] : 0;// i == j的                           时候 dis不存在，所以不考虑。 
                          cnt += i != j ? 1 : 0;// i == j的时候                               dis不存在，所以不考虑。
                    }
               }
        }else{
              for (int i = 0; i < N; i ++)
              node[i].input(fp);
              for (int i = 0; i < N; i ++){
                    dis[i] = new double[N];
                    for (int j = 0; j < N; j ++){
                          dis[i][j] = EUC_2D(node[i],                                         node[j]);// 计算距离
                          tmp += i != j ? dis[i][j] : 0;// i == j的                           时候 dis不存在，所以不考虑。 
                          cnt += i != j ? 1 : 0;// i == j的时候                               dis不存在，所以不考虑。
                     }
              }
       }
        pheromone_0 =  (double)cnt / (tmp *                         N);//pheromone初始值，这里是1 / (avg * N)其中         avg为图网中所有边边权的平均数。
        fclose(fp);
        return;
}

void init(){//初始化
        alpha = 0.1;//evaporation parameter，挥发参             数，每次信息素要挥发的量 
        delta = 1;
        beta = 6;// delta 和 beta分别表示pheromones
        和herustic的比重 
        m = N;
        pheromone = new double*[N + 5];
        herustic = new double*[N + 5];
        info = new double*[N + 5];
        r1 = new int[N + 5];
        r = new int[N + 5];
        s = new int[N + 5];
        J = new set[N + 5];
        empty.clear();
        for (int i = 0; i < N; i ++){
               pheromone[i] = new double[N + 5];
               herustic[i] = new double[N + 5];
               info[i] = new double[N + 5];
               empty.insert(i);
               for (int j = 0; j < N; j ++){
                      pheromone[i][j] = pheromone_0;
                      herustic[i][j] = 1 / (dis[i][j] + eps);//加                         一个小数eps，防止被零除 
                }
         }
         best_so_far.clean();
         iteration = 0;
         MAX = N * N;
}

double power(double x, int y){//快速幂，计算x ^ y，时间复杂度O(logn),感兴趣可以百度 
         double ans = 1;
         while (y){
                 if (y & 1) ans *= x;
                 x *= x;
                 y >>= 1;
          } 
         return ans;
}

void reset(){
         tour = new Tour[m + 5];
         for (int i = 0; i < N; i ++){
                tour[i].clean();
                r1[i] = i;//初始化出发城市， 
               J[i] = empty; 
               J[i].erase(r1[i]);//初始化agent i需要访问的城                市 
               r[i] = r1[i];//当前在出发点 
         }
         for (int i = 0; i < N; i ++)
         for (int j = 0; j < N; j ++){
              info[i][j] = power(pheromone[i][j], delta) *                 power(herustic[i][j], beta);
         }//选择公式 
}

int select_next(int k){
         if (J[k].empty()) return r1[k]; //如果J是空的，那         么返回出发点城市 
        double rnd = (double)(rand()) /                                 (double)RAND_MAX;//产生0..1的随机数 
        set::iterator it = J[k].begin();
        double sum_prob = 0, sum = 0;
        for (; it != J[k].end(); it ++){
              sum += info[r[k]][*it];
        }//计算概率分布 
        rnd *= sum;
        it = J[k].begin();
        for (; it != J[k].end(); it ++){
             sum_prob += info[r[k]][*it];
             if (sum_prob >= rnd){
                    return *it;
             }
         }//依照概率选取下一步城市 
}

void construct_solution(){
       for (int i = 0; i < N; i ++){
            for (int k = 0; k < m; k ++){
                   int next = select_next(k);//选择下一步的                      最优决策 
                   J[k].erase(next);
                   s[k] = next;
                   tour[k].push_back(r[k], s[k]);
                   r[k] = s[k];
             }
       }
}

void update_pheromone(){
       Tour now_best;
       now_best.clean();//初始化 
       for (int i = 0; i < m; i ++){
            tour[i].calc();
            if (tour[i] < now_best)
            now_best = tour[i];//寻找当前迭代最优解 
       }
       if (now_best < best_so_far){
            best_so_far = now_best;//更新最优解 
       }
       for (int i = 0; i < N; i ++)
       for (int j = 0; j < N; j ++)
       pheromone[i][j] *= (1 - alpha);//信息素挥发 
       int sz = now_best.size();
       for (int i = 0; i < sz; i ++){
            pheromone[now_best.r(i)][now_best.s(i)] +=             1. / (double)now_best.L;
            pheromone[now_best.s(i)][now_best.r(i)] =               pheromone[now_best.r(i)][now_best.s(i)];//               对称 
       }//更新信息素含量 
}

int main(){
       srand((unsigned) time(0));//初始化随机种子 
       io();
       init();
       double last = INF;
       int bad_times = 0;
       for (; iteration < MAX; iteration ++){
            if (bad_times > N) break;//进入局部最优 
            reset();//初始化agent信息 
            construct_solution();//对于所有的agent构造               一个完整的tour 
            update_pheromone();//更新信息素 
            printf("iteration %d:best_so_far = %.2lf\n",               iteration, best_so_far.L);
            if (last > best_so_far.L)
            last = best_so_far.L, bad_times = 0;
            else bad_times ++;//记录当前未更新代数，若             迭代多次未更新，认为进入局部最优 
       }
       printf("best_so_far = %.2lf\n", best_so_far.L);//        输出目标值 
       best_so_far.print(stdout);//输出路径 
}
算例演示
例一    满秩矩阵式（type = 1）
输入文件格式为：
File_name            File_type
salesman.in          1
5
0 1 2 2 3
2 0 3 4 2
3 2 0 4 1
3 4 5 0 5
2 4 1 4 0
输出结果为：
opt_solution:
11

例二    二维坐标式（type = 2）
输入文件格式为：
File_name               File_type
KroA100.tsp            2  
100 
1 1380 939
2 2848 96
3 3510 1671
4 457 334
5 3888 666
6 984 965
7 2721 1482
8 1286 525
9 2716 1432
10 738 1325
11 1251 1832
12 2728 1698
13 3815 169
14 3683 1533
15 1247 1945
16 123 862
17 1234 1946
18 252 1240
19 611 673
20 2576 1676
21 928 1700
22 53 857
23 1807 1711
24 274 1420
25 2574 946
26 178 24
27 2678 1825
28 1795 962
29 3384 1498
30 3520 1079
31 1256 61
32 1424 1728
33 3913 192
34 3085 1528
35 2573 1969
36 463 1670
37 3875 598
38 298 1513
39 3479 821
40 2542 236
41 3955 1743
42 1323 280
43 3447 1830
44 2936 337
45 1621 1830
46 3373 1646
47 1393 1368
48 3874 1318
49 938 955
50 3022 474
51 2482 1183
52 3854 923
53 376 825
54 2519 135
55 2945 1622
56 953 268
57 2628 1479
58 2097 981
59 890 1846
60 2139 1806
61 2421 1007
62 2290 1810
63 1115 1052
64 2588 302
65 327 265
66 241 341
67 1917 687
68 2991 792
69 2573 599
70 19 674
71 3911 1673
72 872 1559
73 2863 558
74 929 1766
75 839 620
76 3893 102
77 2178 1619
78 3822 899
79 378 1048
80 1178 100
81 2599 901
82 3416 143
83 2961 1605
84 611 1384
85 3113 885
86 2597 1830
87 2586 1286
88 161 906
89 1429 134
90 742 1025
91 1625 1651
92 1187 706
93 1787 1009
94 22 987
95 3640 43
96 3756 882
97 776 392
98 1724 1642
99 198 1810
100 3950 1558
输出结果为：
best_known_solution: 21282

3.2粒子群算法

粒子群优化算法是在1995年由Eberhart博士和Kennedy博士一起提出的，它源于对鸟群捕食行为的研究。

设想这么一个场景：一群鸟进行觅食，而远处有一片玉米地，所有的鸟都不知道玉米地到底在哪里，但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略，也是最简单有效的策略就是是搜寻目前距离玉米地最近的鸟群的周围区域。粒子群优化算法就是从这种群体觅食的行为中得到了启示，从而构建的一种优化模型。

在粒子群优化算法中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”，而问题的最优解就对应为鸟群要寻找的“玉米地”。所有的粒子都具有一个位置向量（粒子在解空间的位置）和速度向量（决定下次飞行的方向和速度），并可以根据目标函数来计算当前的所在位置的适应值（fitness value），可以将其理解为距离“玉米地”的距离。在每次的迭代中，种群中的粒子除了根据自身的“经验”（历史位置）进行学习以外，还可以根据种群中最优粒子的“经验”来学习，从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代，最终整个种群的粒子就会逐步趋于最优解。

算法应用

Grasshopper优化模块中没有提供群体智能算法，但Grasshopper为开源的软件平台，使用者可以用常用的C#、VB等计算机语言编写属于自己的插件。同时，也有很多已有人编写好的插件，分享在网上。有兴趣的读者，可以找找是否有适合自己的插件。

4总结

如今在结构设计，尤其是结构优化领域，对于算法的应用越来越广泛。以上小i为大家简要介绍了一下常用优化算法的原理，希望大家以后在碰到相应算法时，可以对其有一个宏观的概念。在随后的文章中，小i也会进一步为大家介绍拓扑优化、高度优化、网格优化等常用的结构优化内容和方法。

 

算法提供的是一种处理复杂问题的逻辑，而如何将其应用到实际工程中，还需要工程师去把控。算法就如一把宝剑，通过今天小i的介绍，大家知道了宝剑的出处、锋利度、上手度等，可选择哪把宝剑，并将其应用于实战，还需各位剑客把握。

在实际工程优化过程中，判断优化结果是局部最优解还是全局最优解，如何提高优化计算效率，如何确定优化参数，以及适当的人为干预，都需要工程师依靠力学知识和工程经验判断。不能把优化算法理解为“傻瓜”式的计算工具。