西瓜书重温(一):绪论，可不仅仅是简单介绍

1. 写在前面

这次重温周志华老师的《机器学习》， 第一是找工作需要，第二是内在驱动，自己也确实想学习关于算法的一些底层知识了， 吴军老师在《数学之美》里面说: “技术分为道和术两种， 具体的做事方法是术， 做事的原理和原则是道， 追求术的人一辈子工作很辛苦，而只有掌握了事情的本质和精髓才能在工作中游刃有余”， 西瓜书我觉得应该就是道的层面去总结机器学习， 虽然我感觉这本书对初学者不是很友好 ，因为我第一次读这本书的时候是上一年比这早些时候， 那时候给我的体会是完全不知所云或者是停留在皮毛根本无法深入，即使理解了某些算法的公式推导，所以我并没有耐心看，感觉还不如吴恩达老师的课听得爽哈哈(那时候我并不知道原来机器学习这样学，只是停留在了门槛，连入门都不太算)。所以基于吴恩达老师的课， 这一年来通过一些项目和比赛，慢慢的用上了机器学习，期间时常窃喜原来机器学习算法也不是多么难嘛，调个包就实现了呀，直到一年后的现在，由于面试需要，我又不得不重新揭开这本书读的时候，才真正的发现了这本书的魅力，真的令我折服，也认识到了之前的无知， 仅仅掉包和使用这只能算ML的术，但讲真有些时候我根本不知道为啥要这么用，别人问我，也总是喜欢给它一个优雅的名字叫做“trick”或者称为“玄学”，但我通过这次读发现， 有些东西根本就不是玄学或者所谓的trick， 人家背后都有很强大的理论支撑，还有就是学习的算法目前也只是术层，根本不会结合着业务或算法原理去了解背后的所以然。所以现在学习的感觉就是知识和要做的项目越多，心里就越没有底，不踏实，毕竟玄学和trick不能陪伴我们太长。直到这次重新阅读西瓜书， 才慢慢的开始释然，也让我对机器学习有了新的认知。 所以接下来的这段时间，会重新阅读西瓜书，然后把里面的重要思想(原理层面)，学习的笔记，还有通过这一年的实践对知识点的新理解等进行记录， 把知识进行沉淀， 后期再通过实践不断的补充， 真正去练一波算法内功 。

今天这篇文章对应西瓜书的第一章绪论部分，本来不打算整理的，但是在学习第三章线性回归的时候发现模型自身竟然有归纳偏好一说，也就是我们根据抽样出来的训练集往往会学习到很多个与训练集一致的假设空间(版本空间)，这时候模型会选择哪一个呢？ 这个会由模型的自身"偏好"起作用。 由此概念，我又重新读了下第一章的内容， 顺便把之前一直没弄没明白的"没有免费的午餐"定理也给理解了一下，打通了第一章的几个盲区。所以这篇文章主要是在第一章， 首先是基本的有关于机器学习的概念简单过一下，然后重点整理假设空间，归纳偏好节， 最终梳理下机器学习的发展历程。 相对来说，这篇文章内容较为简单。

大纲如下:

• 有关于机器学习的术语
• 假设空间
• 归纳偏好
• 发展历程

Ok, let’s go!

2. 机器学习的术语

这里是为了知识整理的全面性， 把机器学习中常见的术语统一整理下。

• 数据集: 这个概念比较简单， 我们做机器学习，得到的数据就是数据集， 一般是$m$行$n$列的结构化数据(这里先不管图片或者文本类的非结构化数据哈，先不要较真)， 每一行代表着一条记录，是关于一个事件的描述，称为"样本"或者"示例", 反映事件或者对象在某方面表现或者性质。 而每一列，就是从不同的维度去描述对象的性质，称为"属性"或者"特征"。而属性上的取值称为"属性值"。通过这不同的属性，往往能把每个样本映射到高维空间中的每个点上，而由属性张成的这个空间，叫做"属性空间"，或者"样本空间"或者"输入空间"。 而每个样本的性质，也就是每一行，是由一个向量组成的，所以每个样本也可以称为一个特征向量。 这里我们重点要关注的其实是我们得到的这个数据集其实是整个样本空间的一次采样。
• 模型的学习过程: 从数据中学得模型的过程称为"学习"或者"训练", 这个过程通过执行某个算法完成，训练过程使用的数据称为"训练数据", 学得模型对应了关于数据的某种潜在规律，这个称为"假设"， 这种潜在规律自身，则称为"真相"或者真实。模型学习的过程是为了找出或者逼近真相。这两个概念需要好好体会下。
• 学习器: 学习算法在给定数据和参数空间上的实例化
• 标记: 由于要建立预测模型，那么在训练集中肯定会用样本的"结果"信息，否则模型无法学习， 这些信息称为样本的label， 而这些label的取值，会对应于一个空间，这个空间叫做"标记空间"或者"输出空间"。

当然， 训练数据的标记信息并不是必须存在， 根据训练数据是否拥有标记信息，可以把机器学习任务分为两大类： 监督学习和无监督学习。

• 监督学习: 训练数据的label信息存在，模型的任务是学习数据之间的潜在规律，得到从输入到输出的一种映射关系， 即通过训练集$\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2)...({\mathbf{x}}_{\mathbf{m}},y_m)\}$进行学习，建立一个从输入空间$\mathcal{X}$到输出空间$\mathcal{Y}$的映射: $f:\mathcal{X}\mapsto \mathcal{Y}$, 又根据label是离散或者连续分成了分类或者回归任务。
  • 分类: 预测是值是离散， 又分为二分类或者多分类，二分类中$\mathcal{Y}$通常是$-1,+1$或者是$0,1$, 而多分类中$|\mathcal{Y}|>2$
  • 回归: 预测值是连续值
• 无监督学习: 训练样本本身不具有标记信息， 但我们还是可以用一些方法(比如聚类)把训练集的数据划分为若干个组，学习数据中潜在的规律或者概念。最典型的有聚类，降维，关联等。

机器学习的目标是学得模型能很好的适用于"新样本"， 而不仅仅是训练集上工作很好，即使是聚类这样的无监督学习，也是希望学习到的组能适用于没在训练集中出现的样本。 学得模型适用于新数据的能力，称为"泛化"能力。 强泛化能力的模型，能很好的适应整个样本空间。

假设样本空间的全部样本服从一个未知的"分布"， 我们获得每个样本都是独立的从分布上采样获得的，即"独立同分布"，所以我们希望的是尽管训练集只有样本空间中一个很小的采样，但能很好的反映样本空间的特性，否则就很难期望在训练集上学得的模型在整个样本空间上工作很好。所以两个点:

• 模型在训练集上表现的比较好
• 训练集能很好的体现整个样本空间的数据特性

这样，才能得到一个不错的模型。 一般而言，数据样本更多，得到的关于全体样本分布的信息就会越多，越有可能学习到一个泛化能力强的模型。

3. 假设空间

归纳和演绎是科学推理的两大手段：

• 归纳：从特殊到一般的泛化过程，即从具体的事实归结一般规律
• 演绎：一般到特殊的泛化过程，即从基础原理推演具体情况

显然，机器学习的过程是"从样例中学习普适规律"，这是一个归纳的过程， 归纳学习又有广义和狭义之分， 广义的归纳学习相当于从样例中学习， 而狭义的归纳学习要求从训练数据中学得概念，也称为“概念学习"， 机器学习更是后者。

这里给定一个西瓜数据集(可以根据这个对应下上面的那些概念), 每一样代表一个样本，也是一个西瓜， 色泽，根蒂和敲声描述西瓜的特性，即特征或者叫属性， 好瓜是label。

这个例子的目的是为了解释后面的假设空间。 我们是想根据给定的这几个数据，来学习一个概念，即"好瓜是某种色泽，某种根蒂，某种敲声的瓜"， 那么怎么学习这样的一个概念呢？

我们可以把学习过程看做一个在所有假设组成的空间中进行搜索的过程，搜索目标是找到与训练集"匹配"的假设。 这句话要先体会下，假设可以看做是数据的潜在规律性，模型学习的目标就是这个，那假设有那么多，我们怎么知道哪个是最好的能代表数据规律的呢？ 我们不是从整体样本里面采取了一个训练集吗？ 所以我们就这样认为，如果某个假设能与训练集中的数据匹配，我们就说找到能代表数据规律的假设了(没有办法，只能通过训练集看，毕竟我们不能获得所有数据， 这也就是最好多次采样，得到多个训练集，训练多个模型预测的原因，因为仅仅单凭一个训练集，还真的不能代表整体数据)。

那么， 对于一个简单的例子，比如上面的每个特征都有三种取值，那么再加上*，代表三种里面的某一种， 就相当于每个特征4中取值，这时候得到的假设空间会有$4^3+1$种， 那个1代表空集。 西瓜书上的这个图:

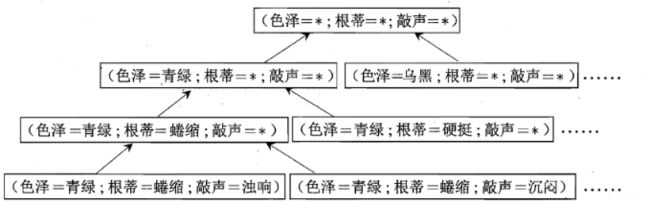
这个的意思是说，由每个特征的取值，我们可以组成这么多个假设空间(64)， 而学习的过程，就是在这些假设空间中，找到匹配训练数据的假设空间， 而由于训练集是有限样本，所以这样找到的假设空间称为"版本空间"。 看看与上面训练集对应的假设空间是哪个呢？ 很不幸，下面三个都可以对应:

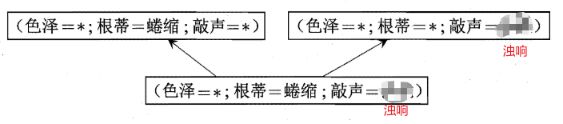
可以看数据集的前两个"好瓜"的特征， 从训练数据看，只要蜷缩，不过其他两个特征是啥，都是好瓜，只要敲声浊响，不过其他两个是啥，都是好瓜，所以上面三个假设其实是都符合的(单从训练集)看。

那么模型学习的时候如何选择呢？ 毕竟虽然上面3个假设都对应训练集，但是面临新样本的时候，对于具体特征不同，输出结果是不同的。这就得说说归纳偏好了。

4. 归纳偏好

对于上面的这个问题， 学习算法本身的"偏好"会起到关键作用， 机器学习算法在学习过程中对某种类型假设的偏好，称为归纳偏好。任何一个有效的机器学习算法都有归纳偏好，否则就选择不出具体的假设来了。那么这玩意有啥用呢？

其实，这东西我们一直在用，只不过我们不知道竟然背后是这样的一个原理罢了，看下面这个图:

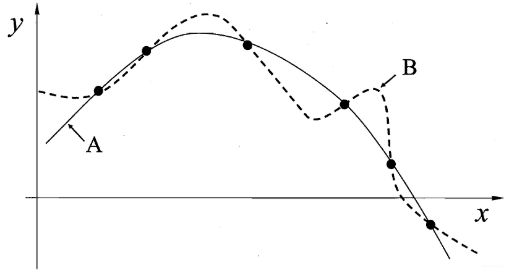
这个图在过拟合的时候是非常常见的一个图了，要学得一个与训练集一致的模型，相当于找到一条线穿过所有的训练集样本点，显然，如果想穿过上面所有的样本点，有很多条曲线，A和B就是其中的两条， 这些曲线其实就对应着上面所说的不同的版本空间。 而我们的学习算法必须有某种偏好，选择其中的一条曲线，才能产出它认为正确的模型。

归纳偏好可看做学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或者“价值观”， 那么有没有一般性的原则来引导算法确定正确偏好呢？ 奥卡姆剃须刀是一种常用的，最基本的原则，即"若有多个假设与观察一致，选择最简单的那个"， 这个可能不太理解，但我们可是经常用呀，加正则化的方式，其实就是引导模型去选择那个较为简单的假设。

归纳偏好对应了学习算法本身所做出的关于"什么样的模型更好"的假设。 在具体现实问题，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定算法是否能取得良好性能。

这里开始出现有意思的一个问题， 那么怎么判断哪个假设是比较简单的呢？ 如果我们直观看上面两个假设，会觉得A比较简单， B比较复杂，所以我们可能会认为产生A假设的算法比产生B假设的算法好， 或者说A的泛化能力强， 但这个绝对吗？

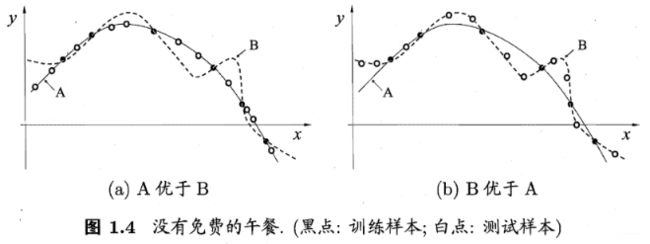
显然，不是绝对的， 就比如b这种情况。这也就是说，对于一个算法${\mathfrak{L}}_a$， 若它在某些问题上比学习算法${\mathfrak{L}}_b$好， 则必存在另一些问题，在那里${\mathfrak{L}}_b$比${\mathfrak{L}}_a$好， 即使${\mathfrak{L}}_a$可能是非常牛的算法，而${\mathfrak{L}}_b$是胡乱猜测的笨拙算法。 这里作者给出了一个证明，看完之后感觉挺吃惊的， 这里是结合着南瓜书来理解的，这里由于涉及到了解释，就手推了。


下面考虑二分类问题，且真实目标函数是任何函数$f$: $\mathcal{X}->\{0,1\}$，函数空间为$\{0,1{\}}^{|\mathcal{X}|}$。对所有可能的$f$按均匀分布对误差求和，有


也就是会发现，总误差竟然与学习算法无关。即对于任意两个学习算法${\mathfrak{L}}_a$和${\mathfrak{L}}_b$，都有
$$\sum _f{E}_{\text{ote }}\left({\mathfrak{L}}_a\mid X,f\right)=\sum _f{E}_{\text{ote }}\left({\mathfrak{L}}_b\mid X,f\right)$$
即无论学习算法${\mathfrak{L}}_a$多聪明或者学习算法${\mathfrak{L}}_b$多笨， 在训练集之外所有样本误差期望是一样的， 这就是"没有免费的午餐定理"(NFL)。 但这个定理的前提是：所有"问题"出现的机会相同或者同样重要，但实际情况中，我们只关注试图解决的问题。

这里换句话说就是，上面的假设是真实目标函数$f$服从的均匀分布，但是实际情况下， 我们只认为高度拟合已有训练样本数据的函数才是真实的目标函数。

所以NFL的寓意很重要， 脱离具体问题，空泛的谈论学习算法好坏毫无意义， 即如果我们不对特征空间有先验的假设，则所有算法的平均表现都一样，要谈论算法的相对优劣，必须针对具体的学习问题才行。所以在一些问题上表现好的算法，在另一些问题上可能不尽如人意， 学习算法自身的归纳偏好与问题是否匹配，往往会起到决定性作用。

不知道有没有这样的体验， 我们在论文里面看到某些高大上的模型之后，往往喜欢直接拿过我们自己的数据进行测试，也就是直接把模型套到我们自己的数据上去，而往往这样会得不到我们期望的效果，这时候，我们可能会抱怨说这模型不行，或者模型的结果并不是论文中那么好，跑不出这样的结果来，再下去，往往下一些错误的判断。

但我们是否想过，我们的数据集是否真的和论文里面的数据集是同样的问题，我们采的数据是否真能代表全体数据，我们采的数据分布是否和人家论文里面的数据分布一致，处理方式是否一样， 模型的参数调整上等，这些方面都有原因的，都得需要好好的思考，切忌轻易的下结论, 也切忌生搬硬套，一定要有自己对算法或者模型的思考以及对数据的洞察。

5. 发展历程

这块就简单一说了，算是科普下：

1. 1950左右，基于神经网络的"连接主义"出现，代表的是感知机模型
2. 1960年左右，基于逻辑表示的"符号主义"学习技术发展
3. 1980年左右，"从样例学习"的符号主义学习成为了主流，代表包括决策树和基于逻辑的学习。
4. 1990年左右， “从样例学习"的神经网络的连接主义也成为了主流， 但BP算法的缺点，就是"黑箱"模型，不可解释，并且最大的局限是"试错性”， 参数的设置缺乏指导，改一点，往往会产生非常不同的结果
5. 1990年中期后，"统计学习"登场并占据主流舞台，代表的是SVM，这是由于连接主义的问题明显，慢慢的人们转向统计学习
6. 21世纪初， 连接主义学习又卷土重来， 深度学习开始蓬勃发展，这时候两大原因，一是数据量上来了，二是计算力上来了。

下面整理机器学习领域的一些会议，竟然西瓜书里面有这个，之前没有看见:

机器学习领域最重要的国际学术会议(顶会哟):

1. 国际机器学习会议(ICML)
2. 国际神经信息处理系统会议(NIPS)
3. 国际学习理论会议(COLT)

重要的区域性会议

• 欧洲机器学习会议(ECML)
• 亚洲机器学习会议(ACML)

重要的国际学术期刊

• journal of Machine Learning Research
• Machine Learning

人工智能领域重要会议和期刊

• IJCAI
• AAAI
• 期刊:
  • Artificial Intelligence
  • Journal of Artificial Intelligence Research

数据挖掘领域的重要会议和期刊

• KDD
• ICDM
• 期刊
  • ACM
  • Transactions on Knowledge Discovery from Data
  • Data Mining and Knowledge Discovery

计算机视觉与模式识别会议和期刊

• CVPR
• 期刊
  • IEEE
  • Transactions on Pattern Analysis and Machine Intelligence

神经网络领域的重要期刊

• Neural Computation
• IEEE Transactions on Neural Networks and Learning Systems

统计学领域重要期刊: Annals of Statistics

好了，关于西瓜书的绪论部分内容差不多就是这些了，比较难理解的是1.4节归纳偏好以及1.3节假设空间， 这些知识可能在实际应用中我们并不是很关心，但了解了这些底层知识之后，更能体会模型的整个学习过程。知道了模型到底在学习啥东西，知道了没有免费的午餐定理，知道了学习算法的归纳偏好要与具体的问题匹配起来。

而这些理论支持的一些实际应用呢？ 比如我们用正则化的方式约束模型参数，就是引导模型去选择一个简单的版本假设，奥卡姆剃须刀的原则。 再比如随机森林从训练集里面进行多次抽样，得到多个训练集，用不同的训练集训练多个模型的集成方式，就是为了能够从多个方面去了解数据，或者用一个训练集训练多个模型， 这些其实都是为了避免这单个训练集不能很好的代替整个样本空间，或者单个模型在这个训练集上学习到的知识可能是片面的，毕竟它有自己的归纳偏好， 训练多个模型， 使得归纳偏好能抵消些。 再或者样本不平衡的时候，我们使用下采样方式的时候，也就是从过多的里面进行采样的时候，也往往是将反例划分为若干个不同集合，提供给学习器，以不会丢失重要信息等。 再或者训练集的数据要尽量和测试集的数据分布一致等等， 这背后都有强大理论支撑的，真不是玄学操作的。

参考：

• 周志华 - 《机器学习》
• 谢文睿 - 《机器学习公式详解》