DataWhale集成学习-Task2
DataWhale集成学习-Task2
-
- 线性回归
-
- 目标函数的数学意义
- 正规方程解决最小二乘问题
- 线性回归推广
- 广义可加模型
- 决策树回归和支持向量回归
记录 DataWhale集成学习的组队学习过程,Task2是熟悉机器学习中的回归问题,主要介绍了三种算法:线性回归;决策树回归;支持向量回归。
线性回归
线性回归,顾名思义就是用线性模型来拟合数据,也就是说假设标签与特征之间存在 y i = θ T x i y_{i}=\boldsymbol{\theta}^{T} \boldsymbol{x_i} yi=θTxi这样的线性关系,线性回归中用的一般都是最小二乘估计,DataWhale的教材中给出了线性回归使用最小二乘回归的两个解释,一个是基于概率的解释,一个是基于几何的解释,这里我也照猫画虎的给出一点自己的见解。
定义一个回归问题:有带标签数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) ⋯ ( x m , y m ) } D=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2)\cdots(\boldsymbol{x_m},y_m)\} D={ (x1,y1),(x2,y2)⋯(xm,ym)},其中 x i ∈ R d \boldsymbol{x_i}\in\mathbb R^d xi∈Rd, m m m个样本的特征组成特征矩阵 X X X,其中 X ∈ R m × d X\in\mathbb R^{m\times d} X∈Rm×d(每一行是一个样本); m m m个样本的标签组成标签向量 y = ( y 1 , y 2 ⋯ y m ) T \boldsymbol{y}=(y_1,y_2\cdots y_m)^T y=(y1,y2⋯ym)T。 我们的目的是求出未知参数 θ \boldsymbol{\theta} θ, 其中, θ ∈ R d \boldsymbol{\theta}\in \mathbb R^d θ∈Rd,使得 ∣ ∣ X θ − y ∣ ∣ 2 2 || X\boldsymbol{\theta}-\boldsymbol{y}||^2_2 ∣∣Xθ−y∣∣22最小。我们记 J ( θ ) = ∣ ∣ X θ − y ∣ ∣ 2 2 J(\boldsymbol{\theta})=|| X\boldsymbol{\theta}-\boldsymbol{y}||^2_2 J(θ)=∣∣Xθ−y∣∣22, J ( θ ) J(\boldsymbol{\theta}) J(θ)就是我们要优化的目标函数。
目标函数的数学意义
第一个要回答的问题就是为什么我们的目标函数要定义为 ∣ ∣ X θ − y ∣ ∣ 2 2 || X\boldsymbol{\theta}-\boldsymbol{y}||^2_2 ∣∣Xθ−y∣∣22这种形式,为什么是残差向量二范数的平方, ∣ ∣ X θ − y ∣ ∣ 2 3 || X\boldsymbol{\theta}-\boldsymbol{y}||^3_2 ∣∣Xθ−y∣∣23这样的三次方不可以吗?这样定义的背后的数学意义在哪里?
这里我们从概率出发,给出一个数学上的解释,我们考虑某单个样本 ( x i , y i ) ( \boldsymbol{x_i},y_i) (xi,yi),在参数 θ \boldsymbol{\theta} θ确定的情况下存在以下公式:
y i = θ T x i + ϵ i (1) y_{i}=\boldsymbol{\theta}^{T} \boldsymbol{x_i}+\epsilon_i \tag{1} yi=θTxi+ϵi(1)
其中, ϵ i \epsilon_i ϵi代表的是误差项,每一个样本都有一个自己的误差项 ϵ \epsilon ϵ,我们将 ϵ \epsilon ϵ看作一个随机变量,在样本间是独立同分布的,而且服从高斯分布 ϵ ∼ N ( 0 , σ 2 ) \epsilon\sim \mathcal{N}(0,\sigma^2) ϵ∼N(0,σ2) 。根据公式(1)我们可知,此时我们是将 θ \boldsymbol{\theta} θ和 x i \boldsymbol{x_i} xi看作已知量的,所以 y i y_i yi也为随机变量,且 y i ∼ N ( θ T x i , σ 2 ) y_i\sim \mathcal{N}(\boldsymbol{\theta}^{T} \boldsymbol{x_i},\sigma^2) yi∼N(θTxi,σ2), y i y_i yi的概率密度函数为:
p ( y i ∣ x i ; θ ) = 1 2 π σ exp ( − ( y i − θ T x i ) 2 2 σ 2 ) (2) p\left(y_i \mid \boldsymbol{x_i} ; \boldsymbol{\theta}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_i-\boldsymbol{\theta}^{T} \boldsymbol{x_i}\right)^{2}}{2 \sigma^{2}}\right) \tag{2} p(yi∣xi;θ)=2πσ1exp⎝⎜⎛−2σ2(yi−θTxi)2⎠⎟⎞(2)
我们知道,标签 y i y_i yi也是独立同分布的,此时已经知道了 y y y的概率分布,接下来就是求未知参数 θ \boldsymbol{\theta} θ,其实也很简单,使用极大似然估计一波带走,先求出似然函数 L ( θ ) L(\boldsymbol\theta) L(θ):
L ( θ ) = log ∏ i = 1 m 1 2 π σ exp ( − ( y i − θ T x i ) 2 2 σ 2 ) = ∑ i = 1 m log 1 2 π σ exp ( − ( y i − θ T x i ) 2 2 σ 2 ) = m log 1 2 π σ − 1 σ 2 ⋅ 1 2 ∑ i = 1 m ( y i − θ T x i ) 2 (3) \begin{aligned}L(\boldsymbol\theta)&=\log \prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_i-\boldsymbol\theta^{T} \boldsymbol x_i\right)^{2}}{2 \sigma^{2}}\right) \\ &=\sum_{i=1}^{m} \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_i-\boldsymbol\theta^{T} \boldsymbol x_i\right)^{2}}{2 \sigma^{2}}\right) \\ &=m \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^{2}} \cdot \frac{1}{2} \sum_{i=1}^{m}\left(y_i-\boldsymbol\theta^{T} \boldsymbol x_i\right)^{2} \end{aligned} \tag{3} L(θ)=logi=1∏m2πσ1exp⎝⎜⎛−2σ2(yi−θTxi)2⎠⎟⎞=i=1∑mlog2πσ1exp⎝⎜⎛−2σ2(yi−θTxi)2⎠⎟⎞=mlog2πσ1−σ21⋅21i=1∑m(yi−θTxi)2(3)
通常顺序是接着对似然函数求导,然后让导数为0,但是从公式(3)我们可以很清楚的看出,要想让 L ( θ ) L(\boldsymbol\theta) L(θ)最大,那 ∑ i = 1 m ( y i − θ T x i ) 2 \sum_{i=1}^{m}\left(y_i-\boldsymbol\theta^{T} \boldsymbol x_i\right)^{2} ∑i=1m(yi−θTxi)2就应该最小,又因为:
∑ i = 1 m ( y i − θ T x i ) 2 = ∣ ∣ X θ − y ∣ ∣ 2 2 (4) \sum_{i=1}^{m}\left(y_i-\boldsymbol\theta^{T} \boldsymbol x_i\right)^{2}=|| X\boldsymbol{\theta}-\boldsymbol{y}||^2_2 \tag{4} i=1∑m(yi−θTxi)2=∣∣Xθ−y∣∣22(4)
有意思的是,我们一开始假设 ϵ ∼ N ( 0 , σ 2 ) \epsilon\sim \mathcal{N}(0,\sigma^2) ϵ∼N(0,σ2) ,最后通过公式化简我们发现,无论 σ \sigma σ取什么值都不影响我们的结论。所以我们至此证明了,最小二乘背后的数学假设是:模型预测的残差服从均值为0的高斯分布。其实以上证明只是Generalize Linear Models模型的一个特殊情况,对Generalize Linear Models感兴趣的朋友可以看一下An Introduction to Generalized Linear Models这篇论文。
正规方程解决最小二乘问题
第一个问题已经解决了,第二问题是如何优化 J ( θ ) J(\boldsymbol{\theta}) J(θ)求出 θ \boldsymbol{\theta} θ,这个问题其实十分好解决,只要遇到一阶可导的优化问题,直接SGD一波带走(大雾),其实如何优化这个问题,涉及到了矩阵论的一些知识(让我回想起了以前被矩阵论课支配的恐惧),内容比较多,这里只做一个最简单的推导。
最小化 ∣ ∣ X θ − y ∣ ∣ 2 2 || X\boldsymbol{\theta}-\boldsymbol{y}||^2_2 ∣∣Xθ−y∣∣22,从矩阵论的角度,可以看作求方程组:
X θ = y (5) X\boldsymbol{\theta}=\boldsymbol{y} \tag{5} Xθ=y(5)
我们知道,当方程组方程的个数大于未知数的个数的时候,方程组称为"超定方程组",是没有解的。在我们这个线性拟合问题中,就是当样本个数 m m m大于特征维度 d d d时,为超定方程组,在绝大时候,样本的个数是远远大于特征的维度的。在矩阵论中,最小二乘问题可以看作这样一个问题:求集合 { θ ∈ R d : ∣ ∣ X θ − y ∣ ∣ i s m i n i m i z e d } \{ \boldsymbol{\theta}\in \mathbb R^d :|| X\boldsymbol{\theta}-\boldsymbol{y}|| \ is\ minimized\} { θ∈Rd:∣∣Xθ−y∣∣ is minimized} ,意思就是,虽然方程组没有解,但是在2范数意义下,存在 θ \boldsymbol{\theta} θ使得 X θ X\boldsymbol{\theta} Xθ最接近 y \boldsymbol y y。其具体求解过程如下:
设残差向量 r = X θ − y \boldsymbol r=X\boldsymbol{\theta}-\boldsymbol{y} r=Xθ−y,我们先在二维空间中进行讨论,此时, X θ X\boldsymbol{\theta} Xθ为一条直线, y \boldsymbol{y} y为空间中的一个向量,根据定义,在 X θ X\boldsymbol{\theta} Xθ这条直线上存在最优点 θ ∗ \boldsymbol{\theta^*} θ∗使得 ∣ ∣ X θ − y ∣ ∣ || X\boldsymbol{\theta}-\boldsymbol{y}|| ∣∣Xθ−y∣∣最小,这个 θ ∗ \boldsymbol{\theta^*} θ∗就是最小二乘解集合中的一个元素,如下图所示:
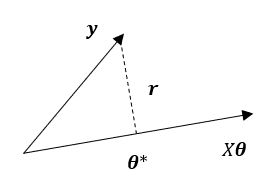
可以很明显的看出,当残差向量 r = X θ − y \boldsymbol r=X\boldsymbol{\theta}-\boldsymbol{y} r=Xθ−y中的 θ = θ ∗ \boldsymbol{\theta}=\boldsymbol{\theta^*} θ=θ∗时, r \boldsymbol r r垂直于 X θ X\boldsymbol{\theta} Xθ。我们知道, X θ X\boldsymbol{\theta} Xθ定义的是矩阵 X X X的列空间 C ( X ) C(X) C(X),由矩阵论中矩阵四个基本空间的知识可知,与 C ( X ) C(X) C(X)垂直的空间为矩阵 X X X的左零空间 N ( X T ) N(X^T) N(XT),所以残差向量 r ∈ N ( X T ) \boldsymbol r\in N(X^T) r∈N(XT),由左零空间的定义可知:
X T r = 0 X^T \boldsymbol r=\boldsymbol 0 XTr=0
将 r = X θ − y \boldsymbol r=X\boldsymbol{\theta}-\boldsymbol{y} r=Xθ−y代入,得到:
X T ( X θ − y ) = 0 X^T(X\boldsymbol{\theta}-\boldsymbol{y})=\boldsymbol0 XT(Xθ−y)=0
最后我们得到The normal equations(正规方程组)
X T X θ = X T y X^TX\boldsymbol{\theta}=X^T\boldsymbol y XTXθ=XTy
解此方程组即可得到最优的参数。
线性回归推广
简单的线性模型只能拟合线性关系,在复杂的数据集中肯定无法取得好的结果,一般的方法是对原始特征进行一些特征映射(feature transform),将原始数据映射到更高维的空间中。像下面这张图一样(图来自林轩田老师的《机器学习基石》课程,一个非常棒的公开课),样本点 { ( x n , y n ) } , n = 1 , 2 , ⋯ \{(\boldsymbol{x_n},y_n)\},n=1,2,\cdots { (xn,yn)},n=1,2,⋯在原始的样本空间中只能用一个圈分割,很显然是线性不可分的,但是通过特征映射,将原始的特征空间 X \mathcal X X映射到空间 Z \mathcal Z Z中,在空间 Z \mathcal Z Z中就成线性可分了。一个大家比较熟悉的应用是SVM中的核函数,起到的作用也是特征映射。

广义可加模型
第一次听说这个模型,公式如下所示,好像是把其他模型得到的结果当作特征,再输入一个线性模型,只不过这个线性模型没有权重,只有一个偏置。感觉这就是集成学习中的Blending和Stacking的一个简化版啊,不知道它们的区别在哪里。 y i = θ 0 + ∑ j f j ( x i ) + ϵ i y_i = {\theta_0} + \sum\limits_{j}f_{j}(x_{i}) + \epsilon_i yi=θ0+j∑fj(xi)+ϵi
决策树回归和支持向量回归
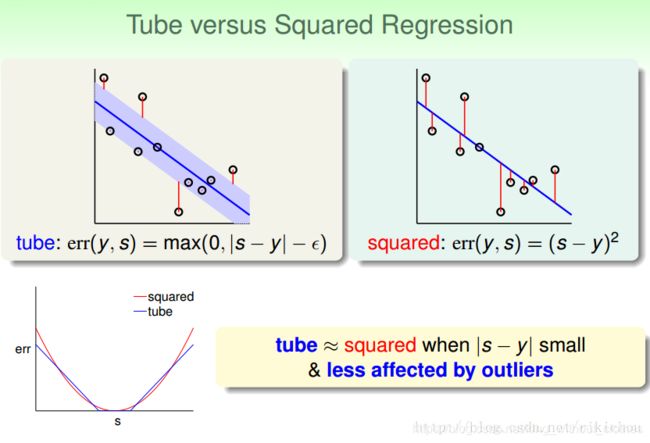
决策树回归就是用一般的决策树做回归问题,常用的还是CART树,关于CART树的知识,《统计学习方法》这本书中给出了很详细的介绍,CART树是GBDT和XGboost的基础。支持向量回归可以参考周志华老师的《机器学习》,和我们上面介绍的线性回归的差别在于损失函数不同,线性回归用平方误差做损失函数,支持向量回归的损失函数设计了一个阈值 ϵ \epsilon ϵ,误差小于这个阈值 ϵ \epsilon ϵ是不计算的,我们还是以林轩田老师课中的图片当例子,图片中的tube函数就是支持向量回归中使用的损失函数,通过加了阈值 ϵ \epsilon ϵ,且使用绝对值作为误差函数,使得算法的抗噪点能力更强。