数据结构与算法---Manacher算法
manacher算法是处理回文子串的一种经典算法。处理回文子串一般使用暴力匹配,动态规划,中心扩散,以及manachar。
在写manacher算法前我们先了解一下中心扩散以及动态规划。暴力匹配比较简单就不再阐述了。
中心扩散法
中心扩散法,顾名思义就是以某一个位置为中心,向周围扩散,直到满足条件或到达边界。中心扩散法的思路是:遍历每一个索引,以这个索引为中心,利用“回文串”中心对称的特点,往两边扩散,看最多能扩散多远。
代码实现:
public String longestPalindrome1(String s) {
//特判
if (s == null || s.length() == 0) {
return "";
}
int strLen = s.length();//字符串长度
int len = 1;//特判未返回说明回文子串长度至少为1
int maxStart = 0;//记录最大回文子串的起始位置索引
int maxLen = 0;//记录最大回文子串的结束位置索引
for (int i = 0; i < strLen; i++) {
int left = i - 1;//左边界
int right = i + 1;//右边界
//首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
while (left >= 0 && s.charAt(left) == s.charAt(i)) {
len++;
left--;
}
//然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
while (right < strLen && s.charAt(right) == s.charAt(i)) {
len++;
right++;
}
//最后左右双向扩散,直到左和右不相等。
while (left >= 0 && right < strLen && s.charAt(right) == s.charAt(left)) {
len = len + 2;
left--;
right++;
}
//如果len大于maxlen就更新maxlen
if (len > maxLen) {
maxLen = len;
maxStart = left;
}
len = 1;
}
//maxStart + 1:因为在执行时向左扩散是直到不相等才停止,所以最长回文子串并不包括索引为maxStart的字符
//maxStart + maxLen + 1:是因为substring()方法是左闭右开区间
return s.substring(maxStart + 1, maxStart + maxLen + 1);
}
中心扩散时间复杂度为O(n²);
空间复杂度为O(1);
动态规划
对于一个子串而言,如果它是回文串,并且长度大于 2,那么将它首尾的两个字母去除之后,它仍然是个回文串。例如对于字符串 “ababa”,如果我们已经知道 “bab” 是回文串,那么 “ababa” 一定是回文串,这是因为它的首尾两个字母都是 ‘a’。
根据这样的思路,我们就可以用动态规划的方法解决本题。我们用 s[i,j] 表示字符串 s 的第 i 到 j 个字母组成的串是否为回文串,二对于不是回文子串又有两种情况:
①:s[i,j] 本身不是一个回文串;
②: i>j,此时 s[i, j] 本身不合法。
也就是说,只有 s[i+1:j-1]是回文串,并且 s 的第 i 和 j 个字母相同时,s[i:j] 才会是回文串。上文的所有讨论是建立在子串长度大于 2 的前提之上的,我们还需要考虑动态规划中的边界条件,即子串的长度为 1 或 2。对于长度为 1 的子串,它显然是个回文串;对于长度为 2 的子串,只要它的两个字母相同,它就是一个回文串。
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
boolean[][] dp = new boolean[len][len];
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= len; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < len; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= len) {
break;
}
//字符不相等显然不是回文串
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
//字符相等且长度小于3时
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
动态规划时间复杂度为O(n²);
空间复杂度为O(n²);
了解了中心扩散和动态规划之后,我们来手撕Manacher!!!
为了表述方便,我们定义一个新概念臂长(也叫回文半径,也可以理解成是中心扩散的步数),表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为 2 * length + 1 ,其臂长为 length。例如“abcba”,字符‘c’最大回文串长度是2*2+1=5,其臂长就是2.
在中心扩散中我们可以得到每一位置的臂长,但在中心扩散法中并没有取利用已知的臂长,而Manacher是怎样利用的呢?
我们用一个变量来记录当前已经出现的回文串的 “最” 右边的索引(maxRight)center则表示这个回文串的中心位置,以及当前位置相对于center对称的位置mirror:
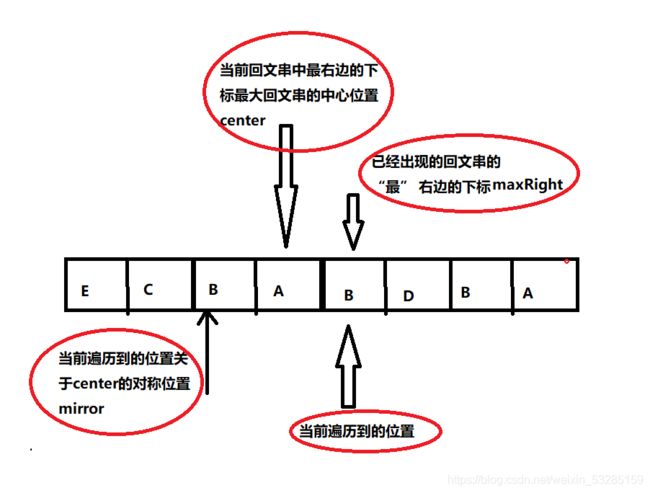
①:包含关系:即当前位置索引小于当前已经出现的回文串的 “最” 右边的索引(maxRight)并且当前位置到回文串的最右侧索引的距离比当前位置关于中心的对称位置的中心扩散的臂长还大(i
如图所示:
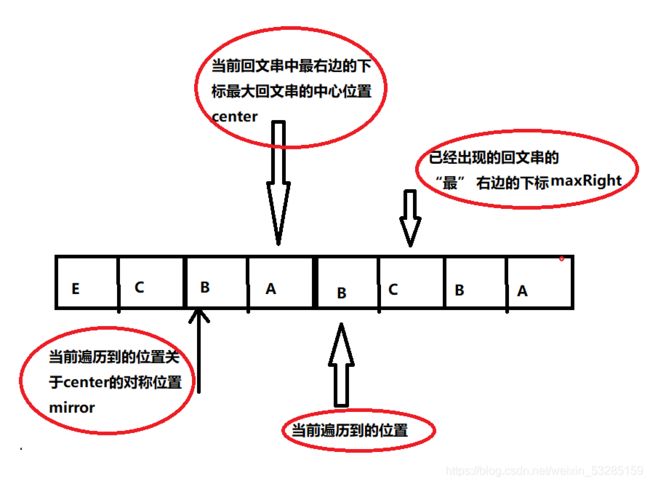
处理方法:
直接返回当前位置关于中心点的对称位置的臂长(arr[i] = arr[mirror])
②:相交,即当前位置索引小于当前已经出现的回文串的 “最” 右边的索引(maxRight)并且当前位置到回文串的最右侧索引的距离小于等于当前位置关于中心的对称位置的中心扩散的臂长(i
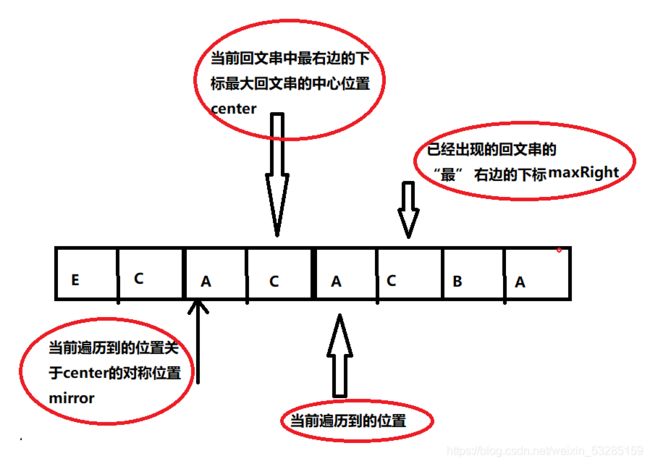
处理方法:返回maxRight-i和arr[mirror]的较小值,(arr[i]=Math.min(maxRight-i,arr[mirror]);)
③:新起点,即当前位置以及是回文串的边界或已经越过边界(maxRight<=i )
如图所示:
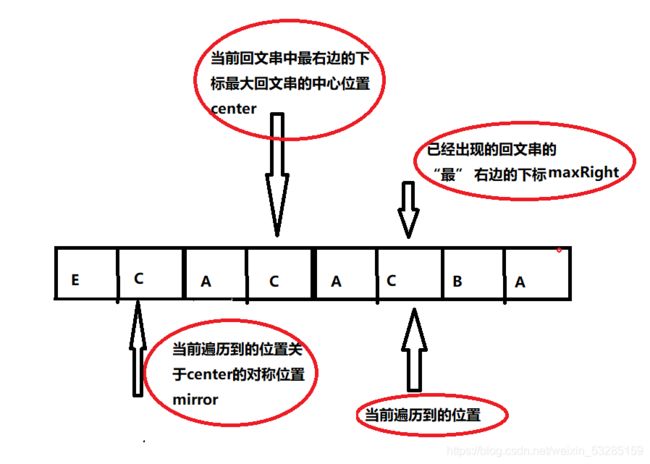
处理方法:进行中心扩散
还有一个字符串长度奇偶数的问题该怎么解决呢?
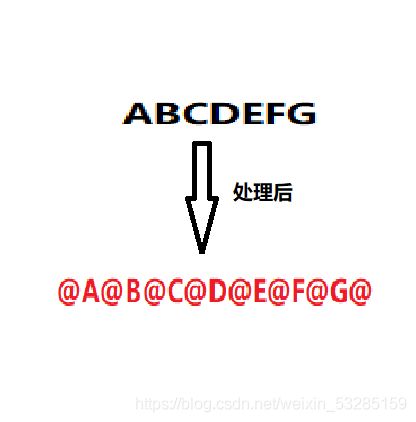
我们可以对字符串进行预处理,在原字符串的前后各加一个特殊字符(比如我的代码实现使用的是‘@’),然后再在原字符串的每个字符间插入这个特殊字符。当字符长度为奇数时。设为2n+1 处理后则是 (2n+1)2+1 结果是奇数;当字符长度为偶数时。设为2n 处理后则是 (2*n)*2+1 结果依然是奇数;这样就解决了字符串长度的奇偶数问题。
代码实现:
public String longestPalindrome(String s) {
int len=s.length()*2+1;
/*对字符串进行预处理
(字符串前后有一个'@'字符,每个字符中间加一个'@'字符,
假设原字符串长度为2n(偶数时),处理后字符串长度为4n+1
假设原字符串长度为2n-1(奇数时),处理后字符串长度为4n-1
也就是无论原字符串长度是奇数还是偶数都可以解决
也就是s.length()*2+1,解决字符串单偶问题)*/
char[] str =new char[len];
str[0]='@';
for(int i=1;i<len;i++){
//奇数时写入字符串s[i/2](因为字符数组读入是读入一个字符再读入一个'@',中间有1跨度)
//偶数时写入'@'
str[i]=i%2==1?s.charAt(i/2):'@';
}
//定义数组arr,arr每个元素是字符串对应下标中心扩散的步数,也可以叫做回文半径
int[] arr= new int[len];
arr[0]=0;//arr[0]左边就是边界无法进行中心扩散,所以步数为0
//回文串的中心centre,回文串最右边下标(已经出现的回文串的 “最” 右边的下标)maxRight
//遍历字符数组时,i关于中心centre对称的点mirror, mirror=2*center-i(因为center=(mirror+i)/2)
int center=0,maxRight=0,mirror=0;
//start 最长回文子串起始位置 ,maxlen最长回文子串的长度
int start=0,maxLen=1;
//循环遍历字符数组,并且更新center以及maxRight
for(int i=1;i<len;i++){
//这一步结合了相容和相交的情况,不去细分两者,而是取两者的共同之处,arr[i]先取当前位置到回文串最右侧的距离与当前位置的对称点的臂长的较小值,然后尝试向两边扩散
if(i<maxRight){
mirror=2*center-i;
arr[i]=Math.min(maxRight-i,arr[mirror]);
}
//尝试进行中心扩散
int left=i-(arr[i]+1);
int right=i+(arr[i]+1);
while(left >= 0 && right < len && str[left] == str[right]){
left--;
right++;
arr[i]++;
}
//更新maxRight以及center
if(i+arr[i]>maxRight){
maxRight=i+arr[i];
center=i;
}
if (arr[i] > maxLen) {
// 记录最长回文子串的长度和相应它在原始字符串中的起点
maxLen = arr[i];
start = (i - maxLen) / 2;
}
}
return s.substring(start,start+maxLen);
}
Manacher算法时间复杂度为O(n);
空间复杂度为O(n);
如有错误欢迎指出,共同进步