第十五章15.1矩阵奇异值分解步骤
文章目录
- 本章内容
- 矩阵的奇异值分解
- 正交矩阵
- 矩阵的奇异值分解
- 矩阵的满秩分解
本课程来自深度之眼,部分截图来自课程视频以及李航老师的《统计学习方法》第二版。
公式输入请参考: 在线Latex公式
本章内容
任务简介:学习矩阵奇异值分解的定义与基本定理,理解奇异值分解的紧凑和截断形式、几何解释、主要性质,掌握奇异值分解的主要步骤。
本章讲了矩阵奇异值分解的基本原理与实现过程。通过学习第1节,理解奇异值分解的定义与性质,掌握奇异值分解基本定理;通过学习第2节,掌握奇异值分解的计算-5步法;第3节描述奇异值分解与矩阵近似的关系,引入弗罗贝尼乌斯范数,矩阵的最优近似和外积展开式。
学习目标:
1.掌握矩阵奇异值分解法原理。
2.理解奇异值分解的两种形式:紧奇异值分解和截断奇异值分解。
3.理解矩阵奇异值分解与的特征值、特征向量的关系。
4.掌握矩阵奇异值分解步骤与几何意义。
5.理解矩阵的弗罗贝尼乌斯范数定义与性质。
矩阵的奇异值分解
SVD可以很容易得到任意矩阵的满秩分
解,⽤满秩分解可以对数据做压缩。
可以⽤SVD来证明对任意 M × N M\times N M×N的矩阵
均存在如下图的分解:
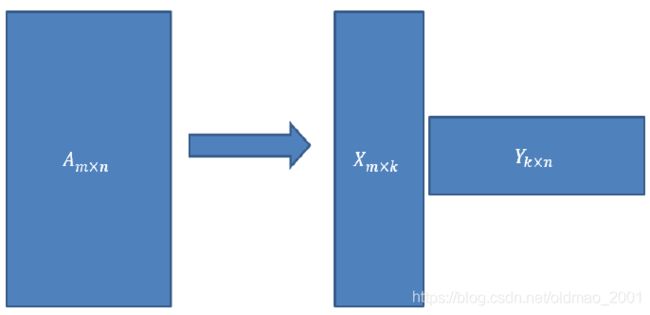
其中 k = r a n k ( A ) k=rank(A) k=rank(A)
这个经常用来数据降维,例如有m个样本,每个样本的维度是n,如果要降维至r维,那么就将m×n矩阵乘以一个n×r的矩阵,就得到m×r的矩阵,达到降维的目的。
注意降维是特征筛选的一种。
正交矩阵
正交矩阵是在欧⼏⾥得空间⾥的名称,在⾣空间⾥被称为⾣矩阵。
⼀个正交矩阵对应的变换叫正交变换,这个变换的特点是不改变向量的尺⼨和向量间的夹⻆。
正交变换是将变换向量⽤另⼀组正交基表示,在这个过程中并没有对向量做拉伸,也不改变向量的空间位置。(可以看成改变是坐标系)
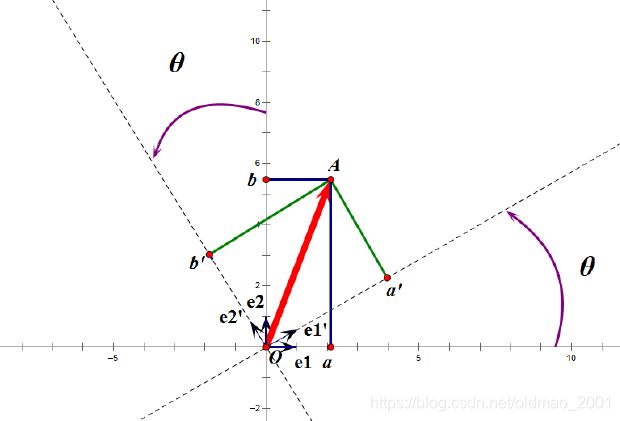
在新坐标系下向量的投影当然是有旋转和变化的。
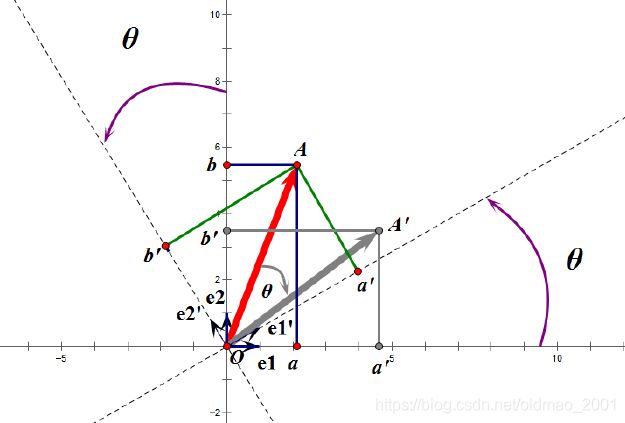
如果选择 e 1 ′ e1' e1′、 e 2 ′ e2' e2′作为新的标准坐标系,那么在新坐标系中OA(原标准坐标系的表示)变成OA’,看起来像坐标系不动,把OA往顺时针⽅向旋转了θ⻆度。
正交矩阵的⾏(列)向量都是两两正交的单位向量,正交矩阵对应的变换为正交变换,它有两种表现:旋转和反射。
正交矩阵将标准正交基映射为标准正交基(即上图中从 e 1 e1 e1、 e 2 e2 e2到 e 1 ′ e1' e1′、 e 2 ′ e2' e2′)
矩阵的奇异值分解
现在假设存在M*N矩阵A,事实上,A矩阵将n维空间中的向量映射到k(k<=m)维空间中,k=Rank(A)。
现在的目标是:在n维空间中找一组正交基,使得经过A变换后还是正交的。假设已经找到这样一组正交基: { v 1 , v 2 … , v n } \{v_1,v_2…,v_n\} { v1,v2…,vn}
则A将这组基映射为: { A v 1 , A v 2 , … , A v n } \{Av_1,Av_2,…,Av_n\} { Av1,Av2,…,Avn}
现在假设存在两组相互正交的基,且其模长为1:
v i T v j = v i ⋅ v j = 0 v_i^Tvj=v_i\cdot v_j=0 viTvj=vi⋅vj=0
所以如果正交基 v v v选择为 A T A A^TA ATA的特征向量的话,由于 A T A A^TA ATA是对称阵, v v v之间两两正交,那么这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化。因为
A v i ⋅ A v i = λ i v i ⋅ v i = λ i Av_i\cdot Av_i=\lambda_iv_i\cdot v_i=\lambda_i Avi⋅Avi=λivi⋅vi=λi
所以有
∣ A v i ∣ 2 = λ i ≥ 0 |Av_i|^2=\lambda_i\ge0 ∣Avi∣2=λi≥0
上面的内容感觉老师讲的和ppt内容相差太远。。。
摘录一点板书内容
如果矩阵 A m × n A_{m\times n} Am×n的秩 r a n k ( A ) = k ≤ min ( m , n ) rank(A)=k\le \min(m,n) rank(A)=k≤min(m,n),那么 A T A A^TA ATA或者 A A T AA^T AAT的秩也是k
证明:
假设矩阵方程 A X = 0 AX=0 AX=0成立
等式两边同时乘以一个东西也成立: A T A X = 0 A^TAX=0 ATAX=0
也就是说X是两个矩阵方程的解,也就是说上面方程的解空间属于下面方程的解空间。
也就是上面方程的解空间维度( n − r a n k ( A ) n-rank(A) n−rank(A))小于下面方程的解空间的维度( n − r a n k ( A T A ) n-rank(A^TA) n−rank(ATA))。
n − r a n k ( A ) ≤ n − r a n k ( A T A ) − r a n k ( A ) ≤ − r a n k ( A T A ) r a n k ( A ) ≥ r a n k ( A T A ) n-rank(A)\le n-rank(A^TA)\\ -rank(A)\le -rank(A^TA)\\ rank(A)\ge rank(A^TA) n−rank(A)≤n−rank(ATA)−rank(A)≤−rank(ATA)rank(A)≥rank(ATA)
上面的方程 A T A X = 0 A^TAX=0 ATAX=0再左右乘以一个东西还是成立的:
X T A T A X = 0 = ∣ ∣ A X ∣ ∣ 2 X^TA^TAX=0=||AX||^2 XTATAX=0=∣∣AX∣∣2
也就是 A X = 0 AX=0 AX=0,从这个推导我们可以得出结论
r a n k ( A ) = r a n k ( A T A ) = r a n k ( A A T ) = rank(A)= rank(A^TA)=rank(AA^T)= rank(A)=rank(ATA)=rank(AAT)=
接上面,由于 A T A , A A T A^TA,AA^T ATA,AAT都是半正定矩阵,因此有k个特征向量,写为:
λ 1 2 ≥ λ 2 2 ≥ ⋯ ≥ λ k 2 \lambda^2_1\ge\lambda^2_2\ge\cdots\ge\lambda^2_k λ12≥λ22≥⋯≥λk2
A v i ⋅ A v i = ∣ ∣ A v i ∣ ∣ 2 = v i T A T A v i Av_i\cdot Av_i=||Av_i||^2=v_i^TA^TAv_i Avi⋅Avi=∣∣Avi∣∣2=viTATAvi
由于 λ 2 \lambda^2 λ2是 A T A A^TA ATA特征值,因此上式可以写为:
= v i T λ i 2 A v i = λ i 2 v i T A v i =v_i^T\lambda_i^2Av_i=\lambda_i^2v_i^TAv_i =viTλi2Avi=λi2viTAvi
由于 v i v_i vi模长是1,因此上面结果为: λ i 2 \lambda_i^2 λi2
为什么可以写成 λ i \lambda_i λi?就好比假设 A = λ i 2 A=\lambda_i^2 A=λi2,这里用 λ i \lambda_i λi来表示A。
∣ A v i ∣ 2 = λ i ≥ 0 |Av_i|^2=\lambda_i\ge0 ∣Avi∣2=λi≥0
得证
取单位向量:
u i = A v i ∣ A v i ∣ = 1 λ i A v i u_i=\cfrac{Av_i}{|Av_i|}=\cfrac{1}{\sqrt{\lambda_i}}Av_i ui=∣Avi∣Avi=λi1Avi
变形:
A v i = σ i u i Av_i=\sigma_iu_i Avi=σiui
其中 σ i = λ i , 0 ≤ i ≤ k , k = R a n k ( A ) \sigma_i=\sqrt{\lambda_i},0\le i\le k,k=Rank(A) σi=λi,0≤i≤k,k=Rank(A)称为奇异值
当 k < i ≤ m k
同样的,对 v 1 , v 2 , ⋯ , v k v_1,v_2,\cdots,v_k v1,v2,⋯,vk进行扩展 v k + 1 , ⋯ , v n v_{k+1},\cdots,v_n vk+1,⋯,vn(这n-k个向量存在于A的零空间中,即Ax=0的解空间的基),使得 v 1 , v 2 , ⋯ , v n v_1,v_2,\cdots,v_n v1,v2,⋯,vn为n维空间中的一组正交基。
则可得到:
A [ v 1 v 2 ⋯ v k ∣ v k + 1 ⋯ v n ] = [ u 1 u 2 ⋯ u k ∣ u k + 1 ⋯ u m ] [ σ 1 0 ⋱ 0 σ k 0 0 0 0 0 ] A[v_1\space v_2\space\cdots\space v_k|v_{k+1}\space\cdots \space v_n]=[u_1\space u_2\space\cdots\space u_k|u_{k+1}\space\cdots \space u_m]\begin{bmatrix} \sigma_1 & & &0 \\ & \ddots& &0 \\ & & \sigma_k&0 \\ 0 & 0 & 0& 0 \end{bmatrix} A[v1 v2 ⋯ vk∣vk+1 ⋯ vn]=[u1 u2 ⋯ uk∣uk+1 ⋯ um]⎣⎢⎢⎡σ10⋱0σk00000⎦⎥⎥⎤
继而可以得到A矩阵的奇异值分解:
A = U Σ V T A=U\Sigma V^T A=UΣVT
矩阵的满秩分解
v i v_i vi为 A T A A^TA ATA的特征向量,称为A的右奇异向量, u i = A v i u_i=Av_i ui=Avi实际上为 A A T AA^T AAT的特征向量,称为A的左奇异向量。下面利用SVD证明矩阵的满秩分解:
A = [ u 1 u 2 ⋯ u k ∣ u k + 1 ⋯ u m ] [ σ 1 0 ⋱ 0 σ k 0 0 0 0 0 ] [ v 1 T ⋮ v k T v k + 1 T ⋮ v n T ] A=[u_1\space u_2\space\cdots\space u_k|u_{k+1}\space\cdots \space u_m]\begin{bmatrix} \sigma_1 & & &0 \\ & \ddots& &0 \\ & & \sigma_k&0 \\ 0 & 0 & 0& 0 \end{bmatrix}\begin{bmatrix} v_1^T\\ \vdots\\ v_k^T\\ v_{k+1}^T\\ \vdots\\ v_n^T\\ \end{bmatrix} A=[u1 u2 ⋯ uk∣uk+1 ⋯ um]⎣⎢⎢⎡σ10⋱0σk00000⎦⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡v1T⋮vkTvk+1T⋮vnT⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
利用矩阵分块乘法展开得:
A = [ u 1 u 2 ⋯ u k ] [ σ 1 ⋱ σ k ] [ v 1 T ⋮ v k T ] + [ u k + 1 ⋯ u m ] [ 0 ] [ v k + 1 T ⋮ v n T ] A=[u_1\space u_2\space\cdots\space u_k]\begin{bmatrix} \sigma_1 & & \\ & \ddots& \\ & & \sigma_k \end{bmatrix}\begin{bmatrix} v_1^T\\ \vdots\\ v_k^T \end{bmatrix}+[u_{k+1}\space\cdots \space u_m]\begin{bmatrix} & & \\ & 0& \\ & & \end{bmatrix}\begin{bmatrix} v_{k+1}^T\\ \vdots\\ v_n^T\\ \end{bmatrix} A=[u1 u2 ⋯ uk]⎣⎡σ1⋱σk⎦⎤⎣⎢⎡v1T⋮vkT⎦⎥⎤+[uk+1 ⋯ um]⎣⎡0⎦⎤⎣⎢⎡vk+1T⋮vnT⎦⎥⎤
可以看到第2项为0:
A = [ u 1 u 2 ⋯ u k ] [ σ 1 ⋱ σ k ] [ v 1 T ⋮ v k T ] A=[u_1\space u_2\space\cdots\space u_k]\begin{bmatrix} \sigma_1 & & \\ & \ddots& \\ & & \sigma_k \end{bmatrix}\begin{bmatrix} v_1^T\\ \vdots\\ v_k^T \end{bmatrix} A=[u1 u2 ⋯ uk]⎣⎡σ1⋱σk⎦⎤⎣⎢⎡v1T⋮vkT⎦⎥⎤
因此得到满秩分解A=XY。