如何确定梯度计算的准确性 调试梯度下降法
关于梯度的调试
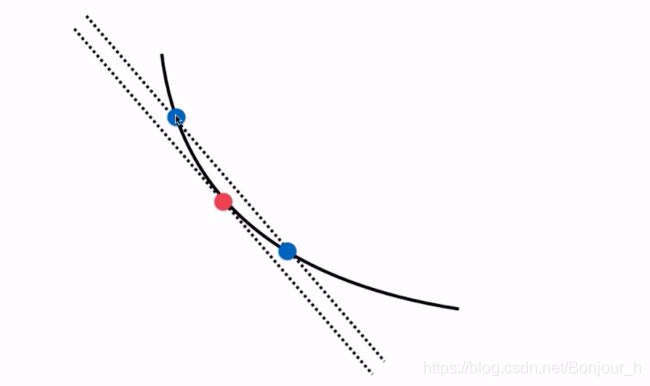 要求红色圆点处的斜率,只需要在图像上该圆点的正方向和负方向一定距离处分别取一个蓝色的点,两个蓝色点连线的斜率就是大致等于红色点的斜率,且距离越小,曲线的斜率就与红色点处的斜率越接近。
要求红色圆点处的斜率,只需要在图像上该圆点的正方向和负方向一定距离处分别取一个蓝色的点,两个蓝色点连线的斜率就是大致等于红色点的斜率,且距离越小,曲线的斜率就与红色点处的斜率越接近。
即在红色点上的倒数就约等于两点在横方向上的差除以两点在纵方向上的差
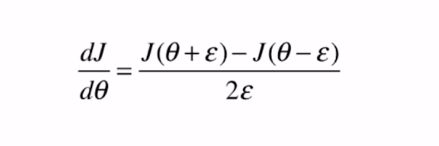
当在高维想对 θ \theta θ求导时,先对 θ 0 \theta _{0} θ0求导,同理对 θ 1 \theta _{1} θ1、 θ 2 \theta _{2} θ2、 θ 3 \theta _{3} θ3… θ n \theta _{n} θn求导,该种方法时间复杂度比较高,仅作为调试的方法

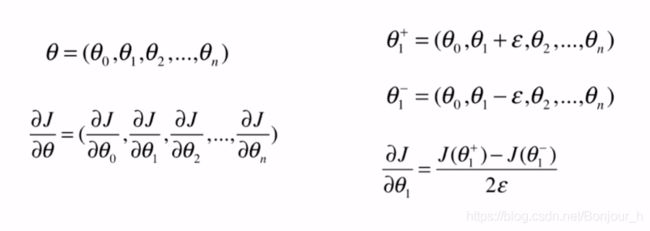
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.random(size=(1000,10))#生成1000个样本,每个样本有10个维度(1000行10列的随机浮点数)
true_theta = np.arange(1,12,dtype=float)#生成1-11的浮点数
X_b = np.hstack([np.ones((len(X),1)),X])
y = X_b.dot(true_theta)+np.random.normal(size=1000)
X.shape
输出:(1000, 10)
y.shape
输出:(1000,)
true_theta
输出:array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
def J(theta,X_b,y):#损失函数
try:
return np.sum((y-X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dJ_math(theta,X_b,y):#求出对于J这个损失函数在theta这个点上的梯度
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def dJ_debug(theta,X_b,y,epsilon=0.01):
res = np.empty(len(theta))
for i in range(len(theta)):
theta_1 = theta.copy()
theta_1[i] += epsilon
theta_2 = theta.copy()
theta_2[i] -= epsilon
res[i] = (J(theta_1,X_b,y) - J(theta_2,X_b,y)) / (epsilon * 2)
return res
def gradient_descent(dJ,X_b,y,initial_theta,eta,n_iters=1e4,epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta,X_b,y)
last_theta = theta
theta = theta - eta * gradient
if(abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < epsilon ):
break
cur_iter += 1
return theta
X_b = np.hstack([np.ones((len(X),1)),X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
#最终得到以dJ_debug作为梯度的求法,使用批量梯度下降法拟合出来的结果
%time theta = gradient_descent(dJ_debug,X_b,y,initial_theta,eta)#最终得到以dJ_debug作为梯度的求法,使用批量梯度下降法拟合出来的结果
theta
输出:Wall time: 1.96 s
array([ 1.07097966, 2.0602673 , 2.92715233, 4.13171709, 5.06055511,
5.91418021, 6.9856838 , 8.00953848, 8.87463983, 9.9956179 ,
10.9168136 ])
#最终得到以dJ_math作为梯度的求法,使用批量梯度下降法拟合出来的结果
%time theta = gradient_descent(dJ_math,X_b,y,initial_theta,eta)
theta
Wall time: 1.2 s
array([ 1.1251597 , 2.05312521, 2.91522497, 4.11895968, 5.05002117,
5.90494046, 6.97383745, 8.00088367, 8.86213468, 9.98608331,
10.90529198])
上述结果说明:
1、dJ_debug的方式是可以使用的,是可以得到正确结果的,只不过速度比较慢
2、dJ_debug函数其实是与J函数无关的,适用于所有的函数,dJ_debug函数完全是可以复用的
而dJ_math只适用于当前任务中对应的特定的损失函数J
3、如果机器学习算法涉及到梯度的求法的时候,我们完全可以先使用dJ_debug这个函数作为梯度的求法,通过这个方式。我们先得到机器学习算法的正确结果,然后再推导公式求出来该梯度计算相应的数学界解,之后将该数学解代入到机器学习算法中,可以通过最终得到的结果和使用dJ_debug得到的结果是否一样来验证我们推导的数学解是否是正确的