基于PyTorch的损失函数

前言

这篇博文为一些常见的损失函数提供了参考，你可以很轻松的导入到代码中。
损失函数定义了神经网络模型如何根据每回合的残差计算总体误差，这反过来又影响它们在进行反向传播时调整系数的方式，因此损失函数的选择直接影响模型的性能。
对于分割和其他分类任务，默认选择的损失函数是二进制交叉熵(BCE)。当一个特定的度量，例如dice系数或IoU，被用来判断模型性能时，竞争对手有时会试验从这些度量派生出的损失函数——通常是形式1 - f(x)，其中f(x)是有问题的度量。这些函数不能简单地用NumPy编写，因为它们是在GPU中实现的，因此需要来自相应模型库的后端函数，其中也包含一个用于反向传播算法的梯度。这并没有想象中复杂。
在多类分割中，通常使用损失函数来计算每个类的平均损失，而不是从整个预测张量中计算损失。这篇博文将作为基本代码的模板参考，但是为了多类平均而修改它应该是很简单的。例如，如果压扁张量包含连续的类，你可以将它们分成四个等长的类，计算它们各自的损失并求平均值。
希望这篇博文对你有所帮助，欢迎你的任何修改建议。

dice loss

骰子系数或Sørensen-Dice系数,是一种常见的标准二进制分类任务,如像素分割,也可以修改作为损失函数:

#PyTorch
class DiceLoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(DiceLoss, self).__init__()

    def forward(self, inputs, targets, smooth=1):
        
        #comment out if your model contains a sigmoid or equivalent activation layer
        inputs = F.sigmoid(inputs)       
        
        #flatten label and prediction tensors
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        
        intersection = (inputs * targets).sum()                            
        dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)  
        
        return 1 - dice

BCE-Dice Loss

这种损失结合了骰子损失和标准的二进制交叉熵(BCE)损失，这通常是默认的分割模型。将这两种方法结合在一起可以在一定程度上减少损失，同时受益于BCE的稳定性。任何学过逻辑回归的人都熟悉多类BCE的方程:

#PyTorch
class DiceBCELoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(DiceBCELoss, self).__init__()

    def forward(self, inputs, targets, smooth=1):
        
        #comment out if your model contains a sigmoid or equivalent activation layer
        inputs = F.sigmoid(inputs)       
        
        #flatten label and prediction tensors
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        
        intersection = (inputs * targets).sum()                            
        dice_loss = 1 - (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)  
        BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
        Dice_BCE = BCE + dice_loss
        
        return Dice_BCE

Jaccard/Intersection over Union (IoU) Loss

IoU指标，或Jaccard指标，类似于骰子指标，计算为两个集合之间的正实例重叠与它们相互组合值之间的比率:

与骰子度量一样，它也是评价像素分割模型性能的常用方法。

#PyTorch
class IoULoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(IoULoss, self).__init__()

    def forward(self, inputs, targets, smooth=1):
        
        #comment out if your model contains a sigmoid or equivalent activation layer
        inputs = F.sigmoid(inputs)       
        
        #flatten label and prediction tensors
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        
        #intersection is equivalent to True Positive count
        #union is the mutually inclusive area of all labels & predictions 
        intersection = (inputs * targets).sum()
        total = (inputs + targets).sum()
        union = total - intersection 
        
        IoU = (intersection + smooth)/(union + smooth)
                
        return 1 - IoU

Focal Loss

Facebook人工智能研究的Lin等人在2017年引入了focal loss，作为对抗极端不平衡数据集的一种手段，在这些数据集中阳性样例相对较少。他们的论文“Focal Loss for Dense Object Detection”可以在这里找到: https://arxiv.org/abs/1708.02002。在实践中，研究人员使用了阿尔法修改版本的函数，所以我将它包含在这个实现中。

#PyTorch
ALPHA = 0.8
GAMMA = 2

class FocalLoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(FocalLoss, self).__init__()

    def forward(self, inputs, targets, alpha=ALPHA, gamma=GAMMA, smooth=1):
        
        #comment out if your model contains a sigmoid or equivalent activation layer
        inputs = F.sigmoid(inputs)       
        
        #flatten label and prediction tensors
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        
        #first compute binary cross-entropy 
        BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
        BCE_EXP = torch.exp(-BCE)
        focal_loss = alpha * (1-BCE_EXP)**gamma * BCE
                       
        return focal_loss

Active-Contour-Loss

https://github.com/lc82111/Active-Contour-Loss-pytorch

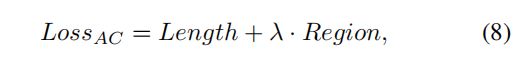
import torch

def active_contour_loss(y_true, y_pred, weight=10):
  '''
  y_true, y_pred: tensor of shape (B, C, H, W), where y_true[:,:,region_in_contour] == 1, y_true[:,:,region_out_contour] == 0.
  weight: scalar, length term weight.
  '''
  # length term
  delta_r = y_pred[:,:,1:,:] - y_pred[:,:,:-1,:] # horizontal gradient (B, C, H-1, W) 
  delta_c = y_pred[:,:,:,1:] - y_pred[:,:,:,:-1] # vertical gradient   (B, C, H,   W-1)
  
  delta_r    = delta_r[:,:,1:,:-2]**2  # (B, C, H-2, W-2)
  delta_c    = delta_c[:,:,:-2,1:]**2  # (B, C, H-2, W-2)
  delta_pred = torch.abs(delta_r + delta_c) 

  epsilon = 1e-8 # where is a parameter to avoid square root is zero in practice.
  lenth = torch.mean(torch.sqrt(delta_pred + epsilon)) # eq.(11) in the paper, mean is used instead of sum.
  
  # region term
  c_in  = torch.ones_like(y_pred)
  c_out = torch.zeros_like(y_pred)

  region_in  = torch.mean( y_pred     * (y_true - C_in )**2 ) # equ.(12) in the paper, mean is used instead of sum.
  region_out = torch.mean( (1-y_pred) * (y_true - C_out)**2 ) 
  region = region_in + region_out
  
  loss =  weight*lenth + region

  return loss