[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)
该系列文章是讲解Python OpenCV图像处理知识,前期主要讲解图像入门、OpenCV基础用法,中期讲解图像处理的各种算法,包括图像锐化算子、图像增强技术、图像分割等,后期结合深度学习研究图像识别、图像分类应用。希望文章对您有所帮助,如果有不足之处,还请海涵~
前面一篇文章介绍了图像增强知识,从而改善图像质量,增强图像识别效果,核心内容分为直方图均衡化、局部直方图均衡化和自动色彩均衡三部分。这篇文章将详细讲解图像分类知识,包括常见的图像分类算法,并介绍Python环境下的贝叶斯图像分类算法、基于KNN算法的图像分类和基于神经网络算法的图像分类等案例。万字长文整理,希望对您有所帮助。 同时,该部分知识均为作者查阅资料撰写总结,并且开设成了收费专栏,为小宝赚点奶粉钱,感谢您的抬爱。当然如果您是在读学生或经济拮据,可以私聊我给你每篇文章开白名单,或者转发原文给你,更希望您能进步,一起加油喔~
代码下载地址(如果喜欢记得star,一定喔):
- https://github.com/eastmountyxz/ImageProcessing-Python
文章目录
- 一.图像分类概述
- 二.常见的分类算法
-
- 1.朴素贝叶斯分类算法
- 2.KNN分类算法
- 3.SVM分类算法
- 4.随机森林分类算法
- 5.神经网络分类算法
- 三.基于朴素贝叶斯算法的图像分类
- 四.基于KNN算法的图像分类
- 五.基于神经网络算法的图像分类
- 六.总结
前文参考:
- [Python图像处理] 一.图像处理基础知识及OpenCV入门函数
- [Python图像处理] 二.OpenCV+Numpy库读取与修改像素
- [Python图像处理] 三.获取图像属性、兴趣ROI区域及通道处理
- [Python图像处理] 四.图像平滑之均值滤波、方框滤波、高斯滤波及中值滤波
- [Python图像处理] 五.图像融合、加法运算及图像类型转换
- [Python图像处理] 六.图像缩放、图像旋转、图像翻转与图像平移
- [Python图像处理] 七.图像阈值化处理及算法对比
- [Python图像处理] 八.图像腐蚀与图像膨胀
- [Python图像处理] 九.形态学之图像开运算、闭运算、梯度运算
- [Python图像处理] 十.形态学之图像顶帽运算和黑帽运算
- [Python图像处理] 十一.灰度直方图概念及OpenCV绘制直方图
- [Python图像处理] 十二.图像几何变换之图像仿射变换、图像透视变换和图像校正
- [Python图像处理] 十三.基于灰度三维图的图像顶帽运算和黑帽运算
- [Python图像处理] 十四.基于OpenCV和像素处理的图像灰度化处理
- [Python图像处理] 十五.图像的灰度线性变换
- [Python图像处理] 十六.图像的灰度非线性变换之对数变换、伽马变换
- [Python图像处理] 十七.图像锐化与边缘检测之Roberts算子、Prewitt算子、Sobel算子和Laplacian算子
- [Python图像处理] 十八.图像锐化与边缘检测之Scharr算子、Canny算子和LOG算子
- [Python图像处理] 十九.图像分割之基于K-Means聚类的区域分割
- [Python图像处理] 二十.图像量化处理和采样处理及局部马赛克特效
- [Python图像处理] 二十一.图像金字塔之图像向下取样和向上取样
- [Python图像处理] 二十二.Python图像傅里叶变换原理及实现
- [Python图像处理] 二十三.傅里叶变换之高通滤波和低通滤波
- [Python图像处理] 二十四.图像特效处理之毛玻璃、浮雕和油漆特效
- [Python图像处理] 二十五.图像特效处理之素描、怀旧、光照、流年以及滤镜特效
- [Python图像处理] 二十六.图像分类原理及基于KNN、朴素贝叶斯算法的图像分类案例
- [Python图像处理] 二十七.OpenGL入门及绘制基本图形(一)
- [Python图像处理] 二十八.OpenCV快速实现人脸检测及视频中的人脸
- [Python图像处理] 二十九.MoviePy视频编辑库实现抖音短视频剪切合并操作
- [Python图像处理] 三十.图像量化及采样处理万字详细总结(推荐)
- [Python图像处理] 三十一.图像点运算处理两万字详细总结(灰度化处理、阈值化处理)
- [Python图像处理] 三十二.傅里叶变换(图像去噪)与霍夫变换(特征识别)万字详细总结
- [Python图像处理] 三十三.图像各种特效处理及原理万字详解(毛玻璃、浮雕、素描、怀旧、流年、滤镜等)
- [Python图像处理] 三十四.数字图像处理基础与几何图形绘制万字详解(推荐)
- [Python图像处理] 三十五.OpenCV图像处理入门、算数逻辑运算与图像融合(推荐)
- [Python图像处理] 三十六.OpenCV图像几何变换万字详解(平移缩放旋转、镜像仿射透视)
- [Python图像处理] 三十七.OpenCV和Matplotlib绘制直方图万字详解(掩膜直方图、H-S直方图、黑夜白天判断)
- [Python图像处理] 三十八.OpenCV图像增强万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)
- [Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)
一.图像分类概述
图像分类(Image Classification)是对图像内容进行分类的问题,它利用计算机对图像进行定量分析,把图像或图像中的区域划分为若干个类别,以代替人的视觉判断。
图像分类的传统方法是特征描述及检测,这类传统方法可能对于一些简单的图像分类是有效的,但由于实际情况非常复杂,传统的分类方法不堪重负。现在,广泛使用机器学习和深度学习的方法来处理图像分类问题,其主要任务是给定一堆输入图片,将其指派到一个已知的混合类别中的某个标签。
在图1中,图像分类模型将获取单个图像,并将为4个标签{cat,dog,hat,mug}分配对应的概率{0.6, 0.3, 0.05, 0.05},其中0.6表示图像标签为猫的概率,其余类比。
如图1所示,该图像被表示为一个三维数组。在这个例子中,猫的图像宽度为248像素,高度为400像素,并具有红绿蓝三个颜色通道(通常称为RGB)。因此,图像由248×400×3个数字组成或总共297600个数字,每个数字是一个从0(黑色)到255(白色)的整数。图像分类的任务是将这接近30万个数字变成一个单一的标签,如“猫(cat)”。
那么,如何编写一个图像分类的算法呢?又怎么从众多图像中识别出猫呢?
这里所采取的方法和教育小孩看图识物类似,给出很多图像数据,让模型不断去学习每个类的特征。在训练之前,首先需要对训练集的图像进行分类标注,如图2所示,包括cat、dog、mug和hat四类。在实际工程中,可能有成千上万类别的物体,每个类别都会有上百万张图像。
图像分类是输入一堆图像的像素值数组,然后给它分配一个分类标签,通过训练学习来建立算法模型,接着使用该模型进行图像分类预测,具体流程如下:
- 输入:输入包含N个图像的集合,每个图像的标签是K种分类标签中的一种,这个集合称为训练集;
- 学习:第二步任务是使用训练集来学习每个类的特征,构建训练分类器或者分类模型;
- 评价:通过分类器来预测新输入图像的分类标签,并以此来评价分类器的质量。通过分类器预测的标签和图像真正的分类标签对比,从而评价分类算法的好坏。如果分类器预测的分类标签和图像真正的分类标签一致,表示预测正确,否则预测错误。
二.常见的分类算法
常见的分类算法包括朴素贝叶斯分类器、决策树、K最近邻分类算法、支持向量机、神经网络和基于规则的分类算法等,同时还有用于组合单一类方法的集成学习算法,如Bagging和Boosting等。
1.朴素贝叶斯分类算法
朴素贝叶斯分类(Naive Bayes Classifier)发源于古典数学理论,利用Bayes定理来预测一个未知类别的样本属于各个类别的可能性,选择其中可能性最大的一个类别作为该样本的最终类别。在朴素贝叶斯分类模型中,它将为每一个类别的特征向量建立服从正态分布的函数,给定训练数据,算法将会估计每一个类别的向量均值和方差矩阵,然后根据这些进行预测。
朴素贝叶斯分类模型的正式定义如下:
该算法的特点为:如果没有很多数据,该模型会比很多复杂的模型获得更好的性能,因为复杂的模型用了太多假设,以致产生欠拟合。
2.KNN分类算法
K最近邻分类(K-Nearest Neighbor Classifier)算法是一种基于实例的分类方法,是数据挖掘分类技术中最简单常用的方法之一。该算法的核心思想如下:一个样本x与样本集中的k个最相邻的样本中的大多数属于某一个类别yLabel,那么该样本x也属于类别yLabel,并具有这个类别样本的特性。简而言之,一个样本与数据集中的k个最相邻样本中的大多数的类别相同。
由其思想可以看出,KNN是通过测量不同特征值之间的距离进行分类,而且在决策样本类别时,只参考样本周围k个“邻居”样本的所属类别。因此比较适合处理样本集存在较多重叠的场景,主要用于预测分析、文本分类、降维等处理。
该算法在建立训练集时,就要确定训练数据及其对应的类别标签;然后把待分类的测试数据与训练集数据依次进行特征比较,从训练集中挑选出最相近的k个数据,这k个数据中投票最多的分类,即为新样本的类别。KNN分类算法的流程描述为如图3所示。
该算法的特点为:简单有效,但因为需要存储所有的训练集,占用很大内存,速度相对较慢,使用该方法前通常训练集需要进行降维处理。
3.SVM分类算法
支持向量机(Support Vector Machine)是数学家Vapnik等人根据统计学习理论提出的一种新的学习方法,其基本模型定义为特征空间上间隔最大的线性分类器,其学习策略是间隔最大化,最终转换为一个凸二次规划问题的求解。
SVM分类算法基于核函数把特征向量映射到高维空间,建立一个线性判别函数,解最优在某种意义上是两类中距离分割面最近的特征向量和分割面的距离最大化。离分割面最近的特征向量被称为“支持向量”,即其它向量不影响分割面。图像分类中的SVM如图4所示,将图像划分为不同类别。
下面的例子可以让读者对SVM快速建立一个认知。给定训练样本,支持向量机建立一个超平面作为决策曲面,使得正例和反例的隔离边界最大化。决策曲面的构建过程如下所示:
第一步,在图5中,想象红球和蓝球为球台上的桌球,首先需要找到一条曲线将蓝球和红球分开,于是得到一条黑色的曲线;
第二步,为了使黑色曲线离任意的蓝球和红球距离最大化,我们需要找到一条最优的曲线,如图6所示;
第三步,假设这些球不是在球桌上,而是抛在空中,但仍然需要将红球和蓝球分开,这时就需要一个曲面,而且该曲面仍然满足所有任意红球和蓝球的间距最大化,如图7所示。离这个曲面最近的红色球和蓝色球就被称为“支持向量(Support Vector)”。
该算法的特点为:当数据集比较小的时候,支持向量机的效果非常好。同时,SVM分类算法较好地解决了非线性、高维数、局部极小点等问题,维数大于样本数时仍然有效。
4.随机森林分类算法
随机森林(Random Forest)是用随机的方式建立一个森林,在森林里有很多决策树的组成,并且每一棵决策树之间是没有关联的。当有一个新样本出现的时候,通过森林中的每一棵决策树分别进行判断,看看这个样本属于哪一类,然后用投票的方式,决定哪一类被选择的多,并作为最终的分类结果。
随机森林中的每一个决策树“种植”和“生长”主要包括以下四个步骤:
- 假设训练集中的样本个数为N,通过有重置的重复多次抽样获取这N个样本,抽样结果将作为生成决策树的训练集;
- 如果有M个输入变量,每个节点都将随机选择m(m
- 每棵决策树都最大可能地进行生长而不进行剪枝;
- 通过对所有的决策树进行加来预测新的数据(在分类时采用多数投票,在回归时采用平均)。
该算法的特点为:在分类和回归分析中都表现良好;对高维数据的处理能力强,可以处理成千上万的输入变量,也是一个非常不错的降维方法;能够输出特征的重要程度,能有效地处理缺省值。
5.神经网络分类算法
神经网络(Neural Network)是对非线性可分数据的分类方法,通常包括输入层、隐藏层和输出层。其中,与输入直接相连的称为隐藏层(Hidden Layer),与输出直接相连的称为输出层(Output Layer)。神经网络算法的特点是有比较多的局部最优值,可通过多次随机设定初始值并运行梯度下降算法获得最优值。图像分类中使用最广泛的是BP神经网络和CNN神经网络。
1.BP神经网络
BP神经网络是一种多层的前馈神经网络,其主要的特点为:信号是前向传播的,而误差是反向传播的。BP神经网络的过程主要分为两个阶段,第一阶段是信号的前向传播,从输入层经过隐含层,最后到达输出层;第二阶段是误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置,具体结构如图8所示。
神经网络的基本组成单元是神经元。神经元的通用模型如图9所示,其中常用的激活函数有阈值函数、Sigmoid函数和双曲正切函数等。
神经元的输出为:
2.CNN卷积神经网络
卷积神经网络(Convolutional Neural Networks)是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习的代表算法之一。卷积神经网络的研究始于二十世纪80至90年代,时间延迟网络和LeNet-5是最早出现的卷积神经网络。在二十一世纪后,随着深度学习理论的提出和数值计算设备的改进,卷积神经网络得到了快速发展,并被大量应用于计算机视觉、自然语言处理等领域。
图10是一个识别的CNN模型。最左边的图片是输入层二维矩阵,然后是卷积层,卷积层的激活函数使用ReLU,即。在卷积层之后是池化层,它和卷积层是CNN特有的,池化层中没有激活函数。卷积层和池化层的组合可以在隐藏层出现很多次,上图中循环出现了两次,而实际上这个次数是根据模型的需要而定。常见的CNN都是若干卷积层加池化层的组合,在若干卷积层和池化层后面是全连接层,最后输出层使用了Softmax激活函数来做图像识别的分类。
三.基于朴素贝叶斯算法的图像分类
本章主要使用Scikit-Learn包进行Python图像分类处理。Scikit-Learn扩展包是用于Python数据挖掘和数据分析的经典、实用扩展包,通常缩写为Sklearn。Scikit-Learn中的机器学习模型是非常丰富的,包括:
- 线性回归
- 决策树
- SVM
- KMeans
- KNN
- PCA
- …
用户可以根据具体分析问题的类型选择该扩展包的合适模型,从而进行数据分析,其安装过程主要通过“pip install scikit-learn”实现。
实验所采用的数据集为Sort_1000pics数据集,该数据集包含了1000张图片,总共分为10大类,分别是人(第0类)、沙滩(第1类)、建筑(第2类)、大卡车(第3类)、恐龙(第4类)、大象(第5类)、花朵(第6类)、马(第7类)、山峰(第8类)和食品(第9类),每类100张。如图11所示。
接着将所有各类图像按照对应的类标划分至“0”至“9”命名的文件夹中,如图12所示,每个文件夹中均包含了100张图像,对应同一类别。
比如,文件夹名称为“6”中包含了100张花的图像,如图13所示。
下面是调用朴素贝叶斯算法进行图像分类的完整代码,调用sklearn.naive_bayes中的BernoulliNB()函数进行实验。它将1000张图像按照训练集为70%,测试集为30%的比例随机划分,再获取每张图像的像素直方图,根据像素的特征分布情况进行图像分类分析。
# -*- coding: utf-8 -*-
# By: Eastmount CSDN 2021-04-01
import os
import cv2
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
#----------------------------------------------------------------------------------
# 第一步 切分训练集和测试集
#----------------------------------------------------------------------------------
X = [] #定义图像名称
Y = [] #定义图像分类类标
Z = [] #定义图像像素
for i in range(0, 10):
#遍历文件夹,读取图片
for f in os.listdir("photo/%s" % i):
#获取图像名称
X.append("photo//" +str(i) + "//" + str(f))
#获取图像类标即为文件夹名称
Y.append(i)
X = np.array(X)
Y = np.array(Y)
#随机率为100% 选取其中的30%作为测试集
X_train, X_test, y_train, y_test = train_test_split(X, Y,
test_size=0.3, random_state=1)
print(len(X_train), len(X_test), len(y_train), len(y_test))
#----------------------------------------------------------------------------------
# 第二步 图像读取及转换为像素直方图
#----------------------------------------------------------------------------------
#训练集
XX_train = []
for i in X_train:
#读取图像
#print i
image = cv2.imread(i)
#图像像素大小一致
img = cv2.resize(image, (256,256),
interpolation=cv2.INTER_CUBIC)
#计算图像直方图并存储至X数组
hist = cv2.calcHist([img], [0,1], None,
[256,256], [0.0,255.0,0.0,255.0])
XX_train.append(((hist/255).flatten()))
#测试集
XX_test = []
for i in X_test:
#读取图像
#print i
image = cv2.imread(i)
#图像像素大小一致
img = cv2.resize(image, (256,256),
interpolation=cv2.INTER_CUBIC)
#计算图像直方图并存储至X数组
hist = cv2.calcHist([img], [0,1], None,
[256,256], [0.0,255.0,0.0,255.0])
XX_test.append(((hist/255).flatten()))
#----------------------------------------------------------------------------------
# 第三步 基于朴素贝叶斯的图像分类处理
#----------------------------------------------------------------------------------
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB().fit(XX_train, y_train)
predictions_labels = clf.predict(XX_test)
print('预测结果:')
print(predictions_labels)
print('算法评价:')
print(classification_report(y_test, predictions_labels))
#输出前10张图片及预测结果
k = 0
while k<10:
#读取图像
print(X_test[k])
image = cv2.imread(X_test[k])
print(predictions_labels[k])
#显示图像
cv2.imshow("img", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
k = k + 1
代码中对预测集的前十张图像进行了显示,其中“368.jpg”图像如图14所示,其分类预测的类标结果为“3”,表示第3类大卡车,预测结果正确。
图15展示了“452.jpg”图像,其分类预测的类标结果为“4”,表示第4类恐龙,预测结果正确。
图16展示了“507.jpg”图像,其分类预测的类标结果为“7”,错误地预测为第7类恐龙,其真实结果应该是第5类大象。
使用朴素贝叶斯算法进行图像分类实验,最后预测的结果及算法评价准确率(Precision)、召回率(Recall)和F值(F1-score)如图16所示。
四.基于KNN算法的图像分类
下面是基于KNN算法的图像分类代码,调用sklearn.neighbors中的KNeighborsClassifier()函数进行实验。核心代码如下:
- from sklearn.neighbors import KNeighborsClassifier
- clf = KNeighborsClassifier(n_neighbors=11).fit(XX_train, y_train)
- predictions_labels = clf.predict(XX_test)
完整代码参照下面的文件。
# -*- coding: utf-8 -*-
# By: Eastmount CSDN 2021-04-01
import os
import cv2
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
#----------------------------------------------------------------------------------
# 第一步 切分训练集和测试集
#----------------------------------------------------------------------------------
X = [] #定义图像名称
Y = [] #定义图像分类类标
Z = [] #定义图像像素
for i in range(0, 10):
#遍历文件夹,读取图片
for f in os.listdir("photo/%s" % i):
#获取图像名称
X.append("photo//" +str(i) + "//" + str(f))
#获取图像类标即为文件夹名称
Y.append(i)
X = np.array(X)
Y = np.array(Y)
#随机率为100% 选取其中的30%作为测试集
X_train, X_test, y_train, y_test = train_test_split(X, Y,
test_size=0.3, random_state=1)
print(len(X_train), len(X_test), len(y_train), len(y_test))
#----------------------------------------------------------------------------------
# 第二步 图像读取及转换为像素直方图
#----------------------------------------------------------------------------------
#训练集
XX_train = []
for i in X_train:
#读取图像
#print i
image = cv2.imread(i)
#图像像素大小一致
img = cv2.resize(image, (256,256),
interpolation=cv2.INTER_CUBIC)
#计算图像直方图并存储至X数组
hist = cv2.calcHist([img], [0,1], None,
[256,256], [0.0,255.0,0.0,255.0])
XX_train.append(((hist/255).flatten()))
#测试集
XX_test = []
for i in X_test:
#读取图像
#print i
image = cv2.imread(i)
#图像像素大小一致
img = cv2.resize(image, (256,256),
interpolation=cv2.INTER_CUBIC)
#计算图像直方图并存储至X数组
hist = cv2.calcHist([img], [0,1], None,
[256,256], [0.0,255.0,0.0,255.0])
XX_test.append(((hist/255).flatten()))
#----------------------------------------------------------------------------------
# 第三步 基于KNN的图像分类处理
#----------------------------------------------------------------------------------
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=11).fit(XX_train, y_train)
predictions_labels = clf.predict(XX_test)
print('预测结果:')
print(predictions_labels)
print('算法评价:')
print((classification_report(y_test, predictions_labels)))
#输出前10张图片及预测结果
k = 0
while k<10:
#读取图像
print(X_test[k])
image = cv2.imread(X_test[k])
print(predictions_labels[k])
#显示图像
cv2.imshow("img", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
k = k + 1
代码中对预测集的前十张图像进行了显示,其中“818.jpg”图像如图17所示,其分类预测的类标结果为“8”,表示第8类山峰,预测结果正确。
图18展示了“929.jpg”图像,其分类预测的类标结果为“9”,正确地预测为第9类食品。
使用KNN算法进行图像分类实验,最后算法评价的准确率(Precision)、召回率(Recall)和F值(F1-score)如图19所示,其中平均准确率为0.63,平均召回率为0.55,平均F值为0.49,其结果略差于朴素贝叶斯的图像分类算法。
五.基于神经网络算法的图像分类
下面是基于神经网络算法的图像分类代码,主要是结合“誓天断发”老师的博客实现的,通过自定义的神经网络实现图像分类。它的基本思想为:先计算每一层的状态和激活值,直到最后一层(即信号是前向传播的);接着计算每一层的误差,误差的计算过程是从最后一层向前推进的(反向传播);最后更新参数(目标是误差变小),迭代前面两个步骤,直到满足停止准则,比如相邻两次迭代的误差的差别很小。
具体代码如下:
# -*- coding: utf-8 -*-
# By: Eastmount CSDN 2021-04-01
import os
import cv2
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
#----------------------------------------------------------------------------------
# 第一步 图像读取及转换为像素直方图
#----------------------------------------------------------------------------------
X = []
Y = []
for i in range(0, 10):
#遍历文件夹,读取图片
for f in os.listdir("photo/%s" % i):
#获取图像像素
Images = cv2.imread("photo/%s/%s" % (i, f))
image=cv2.resize(Images,(256,256),interpolation=cv2.INTER_CUBIC)
hist = cv2.calcHist([image], [0,1], None, [256,256], [0.0,255.0,0.0,255.0])
X.append((hist/255).flatten())
Y.append(i)
X = np.array(X)
Y = np.array(Y)
#切分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, Y,
test_size=0.3, random_state=1)
#----------------------------------------------------------------------------------
# 第二步 定义神经网络函数
#----------------------------------------------------------------------------------
from sklearn.preprocessing import LabelBinarizer
import random
def logistic(x):
return 1 / (1 + np.exp(-x))
def logistic_derivative(x):
return logistic(x) * (1 - logistic(x))
class NeuralNetwork:
def predict(self, x):
for b, w in zip(self.biases, self.weights):
# 计算权重相加再加上偏向的结果
z = np.dot(x, w) + b
# 计算输出值
x = self.activation(z)
return self.classes_[np.argmax(x, axis=1)]
class BP(NeuralNetwork):
def __init__(self,layers,batch):
self.layers = layers
self.batch = batch
self.activation = logistic
self.activation_deriv = logistic_derivative
self.num_layers = len(layers)
self.biases = [np.random.randn(x) for x in layers[1:]]
self.weights = [np.random.randn(x, y) for x, y in zip(layers[:-1], layers[1:])]
def fit(self, X, y, learning_rate=0.1, epochs=1):
labelbin = LabelBinarizer()
y = labelbin.fit_transform(y)
self.classes_ = labelbin.classes_
training_data = [(x,y) for x, y in zip(X, y)]
n = len(training_data)
for k in range(epochs):
#每次迭代都循环一次训练
#训练集乱序
random.shuffle(training_data)
batches = [training_data[k:k+self.batch] for k in range(0, n, self.batch)]
#批量梯度下降
for mini_batch in batches:
x = []
y = []
for a,b in mini_batch:
x.append(a)
y.append(b)
activations = [np.array(x)]
#向前一层一层的走
for b, w in zip(self.biases, self.weights):
#计算激活函数的参数,计算公式:权重.dot(输入)+偏向
z = np.dot(activations[-1],w)+b
#计算输出值
output = self.activation(z)
#将本次输出放进输入列表 后面更新权重的时候备用
activations.append(output)
#计算误差值
error = activations[-1]-np.array(y)
#计算输出层误差率
deltas = [error * self.activation_deriv(activations[-1])]
#循环计算隐藏层的误差率 从倒数第2层开始
for l in range(self.num_layers-2, 0, -1):
deltas.append(self.activation_deriv(activations[l]) * np.dot(deltas[-1],self.weights[l].T))
#将各层误差率顺序颠倒 准备逐层更新权重和偏向
deltas.reverse()
#更新权重和偏向
for j in range(self.num_layers-1):
# 权重的增长量 计算公式为: 增长量 = 学习率 × (错误率.dot(输出值))
delta = learning_rate/self.batch*((np.atleast_2d(activations[j].sum(axis=0)).T).dot(np.atleast_2d(deltas[j].sum(axis=0))))
#更新权重
self.weights[j] -= delta
#偏向增加量 计算公式为: 学习率 × 错误率
delta = learning_rate/self.batch * deltas[j].sum(axis=0)
#更新偏向
self.biases[j] -= delta
return self
#----------------------------------------------------------------------------------
# 第三步 基于神经网络的图像分类处理
#----------------------------------------------------------------------------------
clf = BP([X_train.shape[1],10],10).fit(X_train,y_train,epochs=100)
predictions_labels = clf.predict(X_test)
print('预测结果:')
print(predictions_labels)
print('算法评价:')
print(classification_report(y_test, predictions_labels))
使用神经网络算法进行图像分类实验,最后算法评价的准确率(Precision)、召回率(Recall)和F值(F1-score)如图16-20所示,其中平均准确率为0.63,平均召回率为0.63,平均F值为0.62,整体分类结果良好。
这里可能会疑惑效果为什么会这么差呢?
- 一方面是采用拉直函数,正常图像分类更建议将整个图像矩阵映射进行分类;
- 另一方面我们采用的算法比较传统,后续作者会介绍CNN、RNN、LSTM之类的对比;
- 该篇文章更重要的是普及图像分类算法,并实现一个简单的demo。
六.总结
写到这里,本文就介绍完毕。这篇主要讲解Python环境下的图像分类算法,首先普及了常见的分类算法,包括朴素贝叶斯、KNN、SVM、随机森林、神经网络等,接着通过朴素贝叶斯、KNN和神经网络分别实现了1000张图像的图像分类实验,对读者有一定帮助。
- 一.图像分类概述
- 二.常见的分类算法
1.朴素贝叶斯分类算法
2.KNN分类算法
3.SVM分类算法
4.随机森林分类算法
5.神经网络分类算法 - 三.基于朴素贝叶斯算法的图像分类
- 四.基于KNN算法的图像分类
- 五.基于神经网络算法的图像分类
源代码下载地址,记得帮忙点star和关注喔。
- https://github.com/eastmountyxz/ImageProcessing-Python
时光嘀嗒嘀嗒的流失,这是我在CSDN写下的第八篇年终总结,比以往时候来的更早一些。《敏而多思,宁静致远》,仅以此篇纪念这风雨兼程的一年,这感恩的一年。转眼小宝六个月了,哈哈~这是四月的第一篇文章,加油!
- 2020年总结:敏而多思,宁静致远——纪念这风雨兼程的一年
2020年8月18新开的“娜璋AI安全之家”,主要围绕Python大数据分析、网络空间安全、人工智能、Web渗透及攻防技术进行讲解,同时分享CCF、SCI、南核北核论文的算法实现。娜璋之家会更加系统,并重构作者的所有文章,从零讲解Python和安全,写了近十年文章,真心想把自己所学所感所做分享出来,还请各位多多指教,真诚邀请您的关注!谢谢。
![]()
(By:Eastmount 2021-04-01 晚上12点 http://blog.csdn.net/eastmount/ )
参考文献:
- [1] 罗子江. Python中的图像处理[M]. 科学出版社 2020.
- [2] 冈萨雷斯. 数字图像处理(第3版)[M]. 北京:电子工业出版社, 2013.
- [3] 张恒博, 欧宗瑛. 一种基于色彩和灰度直方图的图像检索方法[J]. 计算机工程, 2004.
- [4] 杨秀璋, 颜娜. Python网络数据爬取及分析从入门到精通(分析篇)[M]. 北京航天航空大学出版社, 2018.
- [5] https://blog.csdn.net/gzq0723/article/details/82185832
- [6] https://blog.csdn.net/baidu_28342107/article/details/82999249.
- [7] https://blog.csdn.net/baidu_28342107/article/details/82870436.
- [8] https://www.jianshu.com/p/57e862d695f2
- [9] ttps://www.jianshu.com/p/6ab6f53874f7
- [10] https://blog.csdn.net/smilejiasmile/article/details/80752889
- [11] https://blog.csdn.net/baidu_28342107/article/details/83307633
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第1张图片](http://img.e-com-net.com/image/info8/755978b23ec14088baba57ef84020a2e.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第2张图片](http://img.e-com-net.com/image/info8/89b86d835d664ded892eb560894b0114.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第3张图片](http://img.e-com-net.com/image/info8/dbfd514b9a9d4ed7b793d3f4244ae1a2.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第4张图片](http://img.e-com-net.com/image/info8/27fbd8b475004cff86dcfee8462740e1.png)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第5张图片](http://img.e-com-net.com/image/info8/259d7c8c69974763b845376479f508a4.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第6张图片](http://img.e-com-net.com/image/info8/ae10494fb8c949c4b084a34be0fd8125.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第7张图片](http://img.e-com-net.com/image/info8/00bbef1fffed4a60bbb61fce298d3c51.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第8张图片](http://img.e-com-net.com/image/info8/4479991ac583457f9c68152b552e39dd.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第9张图片](http://img.e-com-net.com/image/info8/b1272da2b55f4f8d8eaec3d9b906181c.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第10张图片](http://img.e-com-net.com/image/info8/db2b144c2dd34838a8b4026dab3c5f26.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第11张图片](http://img.e-com-net.com/image/info8/e1d6f25d0e184af99a635fb1758c8f98.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第12张图片](http://img.e-com-net.com/image/info8/272f7e2c3f94453a84e4400a62d41483.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第13张图片](http://img.e-com-net.com/image/info8/4b2823d04cbf4634893cc09b3e3d5603.jpg)
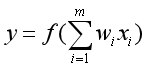
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第14张图片](http://img.e-com-net.com/image/info8/01f924b129664591ac3c3d5d8e657720.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第15张图片](http://img.e-com-net.com/image/info8/03a49ad21bf24e3589ef23c4a0d7817e.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第16张图片](http://img.e-com-net.com/image/info8/2f423182d78d46d9b14a855b6753919d.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第17张图片](http://img.e-com-net.com/image/info8/2310289550494309a000d849a3ec3dab.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第18张图片](http://img.e-com-net.com/image/info8/68a29ddbaf504f4590d2d03b67308095.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第19张图片](http://img.e-com-net.com/image/info8/fa803309f62341738cf579f95c43fa0a.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第20张图片](http://img.e-com-net.com/image/info8/e1a9c21356834b5e9eef7e45529a373a.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第21张图片](http://img.e-com-net.com/image/info8/ec217592695341eb8e90ade218969678.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第22张图片](http://img.e-com-net.com/image/info8/8249c01509084357b43c1e3e0188429a.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第23张图片](http://img.e-com-net.com/image/info8/4d2bad1f92ff4e31b854271d5ee6f015.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第24张图片](http://img.e-com-net.com/image/info8/e8d1cb9b2538479188ab6dbcd1909727.jpg)
![[Python图像处理] 三十九.Python图像分类万字详解(贝叶斯图像分类、KNN图像分类、DNN图像分类)_第25张图片](http://img.e-com-net.com/image/info8/1a65bbc37ac84a46bb7af67c104df705.jpg)