PART.0:
相信每个学过高中生物的同学,都遇到过这么一道欠揍的题目:
“有一家人,有两个孩子,其中一个是女孩,那么另一个是女孩的概率是?”
网上会告诉你答案是1/2,理由是多种多样的,除了“第二个孩子跟第一个孩子什么性别无关,所以是1/2”之外,其它各种说法都貌似很有道理。
而教材上的答案通常会是1/3,理由是基于“贝叶斯”公式的思路,从“男女”、“女男”、“女女”中选择其一。
但是,这些解答其实根本没有接触到背后最实质的问题:很多问题,其实考验的不是“智力”,而是“理解/表达能力”。归根结底,是因为“日常用语”并不是严谨的,而“科学需要的语言”必须是严谨的。
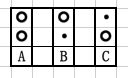
PART.1:[家庭]/[孩子]
先讲个表面上似乎和主题没什么关系的问题:
1.同一个[答案] 回答 不同的[问题]:
“谁爱你”——“我爱你”
“我爱谁”——“我爱你”
2.同一个[问题] 有 不同的[答案]:
“A爱B吗”——“不,A爱C”
“A爱B吗”——“不,D爱B”
对于“我爱你”来说,将焦点放在不同的字上,会有不同的思考模式。我将这种由聚焦不同概念,产生不同思路的现象,暂且命名为某概念[Get Focus]。
“某个[家庭]有两个[小孩]”这个问题,我们将两个不同的点[Get Focus],就会产生两种不同的思路。
PS.1:网上有一种主流的解释方法:
1.「其中一个是女孩」,语义上应该理解为「至少一个是女孩」或者「存在一个是女孩」。
2.「另一个不清楚」的意思,则应该理解为「特指问者知道性别的那个是女孩」。
但是,这其实和问题的描述,是没有什么太大关系的。
因为无论哪种描述方式,其实人们都可以选择两种[Get Focus]的方法来考虑这个问题。
不过是不同的叙述方式,会更加诱导我们倾向于对哪个概念[Get Focus],可是同样的描述对有不同敏感性、不同惯性思维的人来说,能起到的作用是不同的。
PS.2:同样,[贝叶斯]也并没有什么用。
因为当Focus on[家庭]时,贝叶斯是这样的:(1/3)*(0%)+(2/3)*(100%)=[2/3]
但是当Focus on[孩子]时,贝叶斯是这样的:(1/4)*(100%)+(1/4)*(100%)+(1/2)*(0%)=[1/2]
在这个问题下提“贝叶斯”其实没有任何意义。
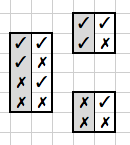
PART.2:[硬币]/[正反面]
如果问题换成了扔硬币,情况是一样的:
PS.3:同样,“先选币后分面”和“先分面后选币”都是在Focus on[硬币组合],答案都会是[2/3]。反之如果Focus on[正反面],无论怎么思考,答案都会是[1/2]
无论给出的描述是什么种类的,答案只跟[Get Focus]有关。
再讲个表面上似乎和主题没什么关系的问题:
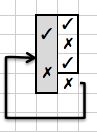
现在的问题是:如果仍一枚硬币,落地后发现朝上的是正面,问另一面是正面的概率?
解释依然众说纷纭:
如果Focus on[硬币],那么[这枚硬币是A硬币的概率是1/3];
如果Focus on[正反面],那么[另一面是正面的概率是1/2]。
PS.4:题目的描述,只会一定程度上改变你Focus的倾向,但是如果确定了Focus on哪一个概念,那么怎样的语言描述都不会影响到这个人的惯性思维了。
我相信这个问题同样有人坚定地认为应该是1/2、1/3,这真的只是[语言理解]带来的问题定性不同而已。
PART.3:成功率
至于还有一种说法是“另一个孩子的性别跟其它无关,就是单纯的1/2,前面的描述都是误导”则有一定的问题。此1/2非彼1/2,数字上的巧合不能代表思考过程的正确。
其实换成另外的思路去看待:
你会发现,此时并不是原始的50%几率能够解决的。
其实可以转换成以下的思路:
那么此时前三种情况的几率分别为:
1/4+(1/4)^2+(1/4)^2+……+(1/4)^n = ?
用+1-1的方法,高中生就可以根据等比公式得出:
1+n+n^2+……n^n = [n^(n-1)-1] / [n-1]
当n趋近无穷时为4/3,4/3-1=1/3
也就是说:
“第二胎(后一胎)”生男生女的几率为[1/3比2/3],而不是各占50%
因为这种情况下和你有了一个“时间机器”是等价的——你没有任何道理地回避了一种自然状况下本来不应该回避的可能性。
End:
其实,网上说的“贝叶斯”、还有其它引申“限定被观察的必须是女孩”、还有说“联合分布”的,这些东西并不是这个问题需要的答案。因为只有[聚焦]才是真正决定不同人有不同思路的主要因素。
我们来考虑一下:将最前面的问题进行修改会如何?
“我爱她” = > 问题可以同时指向“我爱的人是谁”、“爱她的人是谁”
“我是爱她的人” = > 问题很难指向“我爱的人是谁”
“我爱的人是她” = > 问题很难指向“爱她的人是谁”
“A爱B吗?” = > 答案可以同时指向“不,A爱C”、“不,D爱B”
“A爱的人是B吗?” = > 答案很难指向“不,D爱B”
“A是爱B的人吗?” = > 答案很难指向“不,A爱C”
但是就算如此,“A是爱B的人吗?”这个问题依然有人会回答“不,A是爱C的人”。
当一个人坚定地聚焦某个概念,你是很难改变他的思维的。