逐步回归选取特征及GAM模型的使用==college数据集（统计学习导论）

统计学习导论习题 chapter 7 EX-10

Author - - SIHENG HUANG
Attention：**切勿直接copy入作业 **

问题复现

数据集下载链接：college数据集

【问题分析一】 逐步回归选取特征

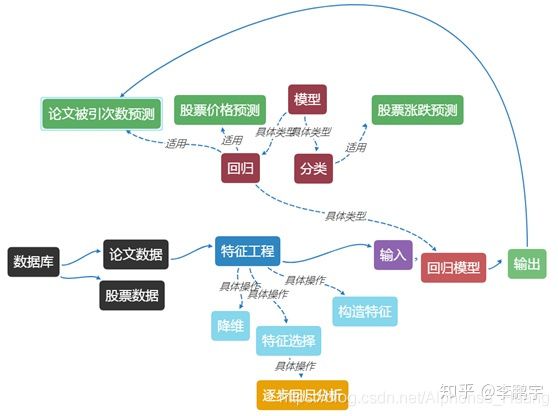
逐步回归分析的名字里虽然带了“回归”，但实际上是一个特征选择方法。如图，是与逐步回归分析相关的一些概念及其关系。

Resource — 知乎

基于逐步回归分析的特征选择

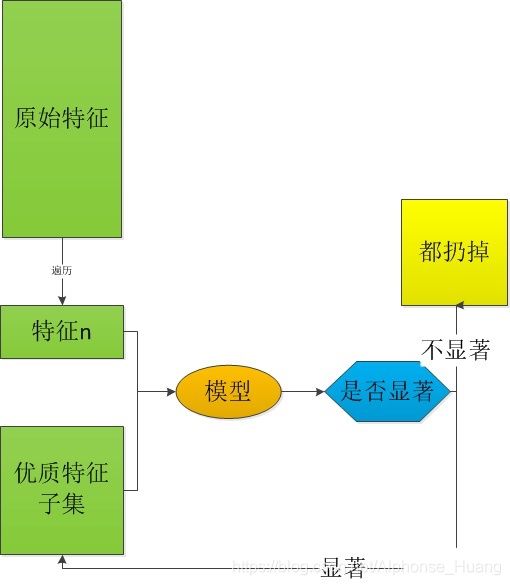
逐步回归分析的过程如下图，

主要的步骤包括：

(1) 从原始特征集合中，不放回地随机选择一个特征;

(2) 将这个特征与特征子集合起来，建回归模型，并进行统计检验;

(3) 如果得到一个显著的模型，说明这个特征是有用的，将这个特征收录到特征子集中；如果模型不显著，说明这个特征没用，需要删掉。

遍历完原始特征集合，我们就得到了一个优质的特征子集，以及一个显著的回归模型。

逐步回归就这么一点内容:它首先是一个特征选择的策略，然后还有建立回归模型的功能。

逐步回归分析的python实现

逐步向前回归算法的python实现

def forward_stepwise_selection(data,target):
    
    total_features = [[]]
    score_dict = {
     }
    remaining_features = [col for col in data.columns if not col == target]
    
    for i in range(1,len(data.columns)):
        best_score = 0;best_feature = None
        for feature in remaining_features:

            X = total_features[i-1] + [feature]
            model = LinearRegression().fit(data[X],data[target])
            score = r2_score(data[target],model.predict(data[X]))

            if score > best_score:
                best_score = score
                best_feature = feature
        
        total_features.append(total_features[i-1] + [best_feature])
        remaining_features.remove(best_feature)
        score_dict[i] = best_score
    
    return total_features,score_dict

应用到本例

total_features_fwd, score_dict_fwd = forward_stepwise_selection(data,'Outstate')

X_train,X_test,y_train,y_test = train_test_split(data.drop('Outstate',axis = 1),data['Outstate'],test_size = 0.2)

validation_scores_dict = {
     }
for features in total_features_fwd[1:]:
    lr = LinearRegression()
    lr.fit(X_train[features],y_train)
    preds = lr.predict(X_test[features])
    validation_scores_dict[len(features)] = mean_squared_error(y_test,preds)

选取特征

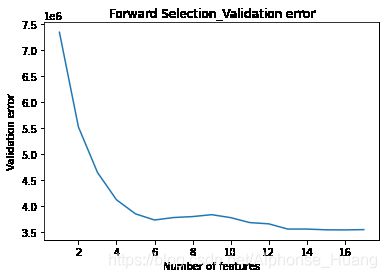
# By Validation error
plt.plot(list(validation_scores_dict.keys()),list(validation_scores_dict.values()))
plt.xlabel('Number of features')
plt.ylabel('Validation error')
plt.title('Forward Selection_Validation error')

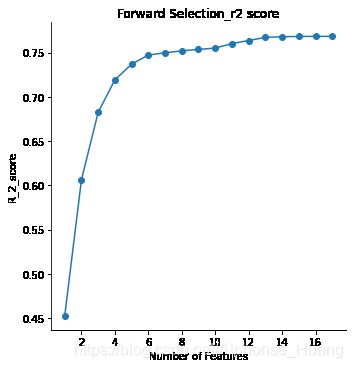
# By r2 score
temp = pd.DataFrame({
     'Number of Features':np.arange(1,len(total_features_fwd)),
                     'R_2_score':list(score_dict_fwd.values())})
plt.figure(figsize = (12,6))
g = sns.FacetGrid(data = temp,size=5)
g.map(plt.scatter, 'Number of Features' , 'R_2_score')
g.map(plt.plot, 'Number of Features', 'R_2_score')
plt.xticks = list(np.arange(1,len(total_features_fwd)))
plt.title('Forward Selection_r2 score')

结果输出：根据R2及validation_scores选取

features_selected = total_features_fwd[13]

最后，选取了如下特征：
'Expend',
 'Private',
 'Room.Board',
 'perc.alumni',
 'PhD',
 'Grad.Rate',
 'Personal',
 'Terminal',
 'S.F.Ratio',
 'Accept',
 'F.Undergrad',
 'Apps',
 'Top10perc'

【问题分析二】GAM

广义相加模型通过光滑样条函数 、核函数或者局部回归光滑函数，对变量进行拟合。GAM采用模型中的每个预测变量并将其分成多个部分（由’结’​​分隔），然后将多项式函数分别拟合到每个部分。GAM的原理是最小化残差（拟合优度）同时最大化简约性（最低可能自由度）。回归模型中部分或全部的自变量采用平滑函数，降低线性设定带来的模型风险，对模型的假定不严，如不需要假定自变量线性相关于因变量（线性或非线性都可以），并且解决logistic回归当解释变量个数较多时容易引起维度灾难（Curse of dimensionality）。

GAM的python实现

模型建立

from pygam import LinearGAM,LogisticGAM
from sklearn import preprocessing

# Standardized the y_value
data["Outstate"] = preprocessing.MinMaxScaler(feature_range=(0, 1), copy=True).fit_transform(data[["Outstate"]])

X = data[features_selected]
y = pd.Series(data.Outstate)

# Split data
X_train,X_test, y_train, y_test = train_test_split(X,y,test_size=0.2, random_state=0)
# --- time warning 【about 27min】 ---  
lam = np.logspace(-3, 3, 2)
lams = [lam] * 13
gam = LogisticGAM().fit(X_train, y_train)
gam = gam.gridsearch(X_train, y_train,lam = lams)                                           

模型评估

from sklearn.metrics import mean_squared_error,r2_score

predictions = gam.predict_proba(X_test)      
print("Accuracy: {} ".format(mean_squared_error(y_test, predictions)))
print("Fitting score: {} ".format(r2_score(y_test, predictions)))

Accuracy: 0.009899192760988572
Fitting score: 0.7889358717146394

GAM模型 — 自动调参

通过gridsearch来自动选择参数。默认参数是一个字典类型的lam，{‘lam’:np.logspace(-3,3,11)}

有2种方式：

• 通过网格，将grid变成list，搜寻的数量一共有2**13个。（13个特征）

lam = np.logspace(-3, 3, 2)
lams = [lam] * 13
gam.gridsearch(X, y, lam=lams)

• 直接将网格变成np.ndarray，当搜索的空间非常大的时候，我们会随机进行搜索。

lams = np.exp(np.random.random(50, 4) * 13 - 3)
gam.gridsearch(X, y, lam=lams)

GAM模型的解释—部分依赖图（Partial dependency plots）

gam的优势之一是，gam的可加性让我们能够控制其他变量，来探究和解释某一个变量。通过generate_X_grid来帮助我们产生合适的画图数据。

如果我们非常想要结合这些图像的可解释性，并且防止GAM过拟合，从而提出一个能够推广到持久数据集的模型，则需要引入部分依赖图。

部分依赖图（Partial dependency plots）非常有用，因为他们具有高度的可解释性，并且易于理解。

LINK：部分依赖图用于解释数据

关于本例

# Partial dependency plots
plt.rcParams['figure.figsize'] = (20, 10)
fig, axs = plt.subplots(1,13)
titles = features_selected

for i, ax in enumerate(axs):
    XX = gam.generate_X_grid(term=i)
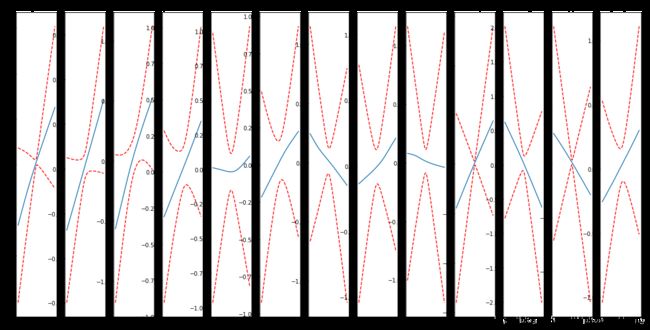
    ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX))
    ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX, width=.95)[1], c='r', ls='--')
    ax.set_title(titles[i])
    
plt.show()

输出

因此，对该图进行解释，便得到自变量特征及目标特征的关系。

同时，不妨尝试用Poly Regression, 并把degree设置为3，预计会有较强的线性性。

部分依赖图 ---- 调整光滑度

对于有些很难解释特征，并且我们已经推断我们希望有一条更平滑的曲线。（有先验知识的情况下，我们通过设置约束，强制让某一个特征对目标值有着单调递增或递减的特性，或者调整样条函数的数量。）

主要调整的参数有三个，n_splines，lam，和constraints。

• n_splines：用来拟合的spline函数（样条函数）的数量
• lam：惩罚项（在整个目标函数中乘以二阶导数）
• constraints：允许用户指定函数是否应具有单调约束的约束列表。包括[‘convex’, ‘concave’,‘monotonic_inc’, ‘monotonic_dec’,’circular’, ‘none’]

更改n_splines让曲线变得更光滑。（如果惩罚项对于每一个特征都是一样的值，则不需要写成list形式；如果不一样的值，那么可以写成列表）

如果我们强制平滑后，准确度下降了，说明我们损失了一部分信息（没有捕捉到部分信息），不过同样，准确度的下降也表明我们可以将多少我们的直觉加入到模型中。

参数lam控制着惩罚程度，就算我们将n_splines设置的很大，但是惩罚很大的话，函数图像可能仍然会出现直线。