一、实验目的
1、学习K-means算法,理解算法的原理及其过程。
2、选择合适的实验,进行算法的仿真重现。
二、算法基本原理及其内容
K-means算法是基于原型的、划分的聚类技术。它试图发现用户指定个数(K)的簇(由质心代表)。K-means算法比较简单,基本算法原理如下:
首先,选择K个初始质心,其中K是用户指定的参数,即所期望的簇的个数。每个点指派到最近的质心,而指派到一个质心的点集为一个簇。
然后,根据指派到簇的点,更新每个簇的质心。
重复指派和更新步骤,直到簇不发生变化,或等价地,直到质心不发生变化。
三、实验步骤
那么在计算机编程中,其算法步骤一般如下:
1)随机生成随机点簇
2)从D中随机取k个元素,作为k个簇的各自的中心。
3)分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。
4)根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。
5)将D中全部元素按照新的中心重新聚类。
6)重复第4步,直到聚类结果不再变化。
7)将结果输出。
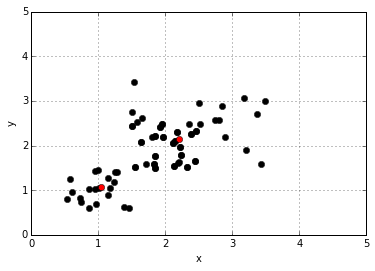
四、实验结果
import matplotlib.pyplot as plt
import numpy as np
culster1 = np.random.uniform(0.5, 1.5, (2, 20))
culster2 = np.random.uniform(1.5, 2.5, (2, 20))
culster3 = np.random.uniform(1.5, 3.5, (2, 20))
culster4 = np.random.uniform(3.5, 4.5, (2, 20))
x1 = np.hstack((culster1,culster2))
x2 = np.hstack((culster2,culster3))
x = np.hstack((x1,x2)).T
plt.figure()
plt.axis([0, 5, 0, 5])
plt.xlabel(‘x‘)
plt.ylabel(‘y‘)
plt.grid(True)
plt.plot(x[:,0],x[:,1], ‘k.‘, markersize = 12)
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
kmeans = KMeans(n_clusters = 2)
kmeans.fit(x)
plt.plot(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],‘ro‘)
K = range(1, 10)
meandistortions = []
for k in K:
kmeans =KMeans(n_clusters=k)
kmeans.fit(x)
meandistortions.append(sum(np.min(cdist(x, kmeans.cluster_centers_,‘euclidean‘), axis=1)) / x.shape[0])#选择每行最小距离求和
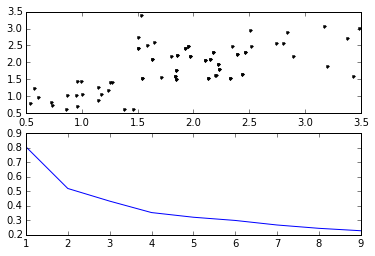
plt.figure()
plt.grid(True)
plt1 = plt.subplot(2,1,1)
plt1.plot(x[:,0], x[:,1], ‘k.‘)
plt2 = plt.subplot(2,1,2)
plt2.plot(K, meandistortions)
五、实验结果
六、总结
实验主要学习了K-means算法原理及其实现过程的学习。理解了K-means算法核心的内容要点。如何找到质心、计算质心等。但仍存在不足,后续会学习二分K-means算法及其他聚类算法,比较相同点和不同点,比较适用范围及其优劣等。