【物流选址】佛洛依德算法求解物流选址问题【Matlab 108期】

一、简介

1 弗洛伊德(Floyd)算法介绍
1)和Dijkstra算法一 样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵 奖获得者、斯坦福大学计算机科学系教授罗伯特.弗洛伊德命名
2)弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
3)迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径。
4)弗洛伊德算法VS迪杰斯特拉算法:迪杰斯特拉算法通过选定的被访问项点，求出从出发访问顶点到其他项点的最短路径;弗洛伊德算法中每个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他项点的最短路径。

2 弗洛伊德(Floyd)算法最佳应用-最短路径

1)胜利乡有7个村庄(A,B,C,D,E,E, G)
2)各个村庄的距离用边线表示(权)，比如A-B距离5公里
3)问:如何计算出各村庄到其它各村庄的最短距离?

3 弗洛伊德(Floyd)算法图解分析
1)设置顶点vi到顶点vk的最短路径己知为Lik，顶点vk到vj的最短路径已知为Lkj，顶点vi到vj的路径为Lij，则vi到vj的最 短路径为: min((Lik+Lkj),Lij)， vk的取值为图中所有顶点，则可获得vi到vj的最短路径
2)至于vi到vk的最短路径Lik或者vk到vj的最短路径Lkj,是以同样的方式获得
3)弗洛伊德(Floyd)算法图解分析举例说明
3.1 弗洛伊德算法的步骤:
初始状态：

第一轮循环中，以A(下标为: 0)作为中间顶点[即把A作为中间顶点的所有情况都进行遍历,
就会得到更新距离表和前驱关系]，距离表和前驱关系更新为:

将A做为中间顶点的情况有：
C->A->G:9,C->G:N
C->A->B:12,C->B:N
G->A->B:7,G->B:3
通过比较，得出最小的值，然后更新距离表和前驱关系表
以此类推。。。

4 案例
某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系a，b表示，距离单位：千米）及水泥日用量d（吨）由下表给出。目前急需新建两个料场，位置待定，日储量各有20吨。假设从料场到工地之间均有直线道路相连。试制定两个料场的位置以及每天的供应计划，即从A，B两料场分别向各工地运送多少吨水泥，使得总的运输吨千米数最小。

二、源代码

x0 = [3.0000  5.0000  0.0707  7.0000  0  0.9293  0  0  3.9293  0  6.0000 ...
      10.0707  6.3875  4.3943  5.7511  7.1867]';
A=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
b=[20;20];
Aeq=[1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0;...
       0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0;...
       0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0;...
       0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0;...
       0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0;...
       0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0];
beq=[3;5;4;7;6;11];
VLB=[0;0;0;0;0;0;0;0;0;0;0;0];
VUB=[];
[x,fval]=fmincon('f1',x0,A,b,Aeq,beq,VLB,VUB)
function [x,val,k]=bfgs(fun,gfun,x0,varargin)
%功能: 用BFGS算法求解无约束问题:  min f(x)
%输入: x0是初始点, fun, gfun分别是目标函数及其梯度;
% varargin是输入的可变参数变量, 简单调用bfgs时可以忽略它,
% 但若其它程序循环调用该程序时将发挥重要的作用
%输出:  x, val分别是近似最优点和最优值,  k是迭代次数.
maxk=500;   %给出最大迭代次数
rho=0.55; sigma1=0.4; epsilon1=1e-5; 
k=0;   n=length(x0); 
Bk=eye(n);   %Bk=feval('Hess',x0); 
while(k<maxk)
    gk=feval(gfun,x0,varargin{
     :}); %计算梯度
    if(norm(gk)<epsilon1), break; end  %检验终止准则
    dk=-Bk\gk;  %解方程组, 计算搜索方向
    m=0; mk=0;
    while(m<20)   % 用Armijo搜索求步长 
        newf=feval(fun,x0+rho^m*dk,varargin{
     :});
        oldf=feval(fun,x0,varargin{
     :});
        if(newf<oldf+sigma1*rho^m*gk'*dk)
            mk=m; break;
        end
        m=m+1;
    end
    %BFGS校正
    x=x0+rho^mk*dk;  
    sk=x-x0;  yk=feval(gfun,x,varargin{
     :})-gk;
    if(yk'*sk>0)
        Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);
    end
    k=k+1;     x0=x;
end
function g=df1(x)
g = [sqrt((x(13)-1.25)^2+(x(14)-1.25)^2), sqrt((x(13)-8.75)^2+(x(14)-0.75)^2),...
    sqrt((x(13)-0.5)^2+(x(14)-4.75)^2), sqrt((x(13)-5.75)^2+(x(14)-5.0)^2),...
    sqrt((x(13)-3.0)^2+(x(14)-6.5)^2), sqrt((x(13)-7.25)^2+(x(14)-7.25)^2),...
    sqrt((x(15)-1.25)^2+(x(16)-1.25)^2), sqrt((x(15)-8.75)^2+(x(16)-0.75)^2),...
    sqrt((x(15)-0.5)^2+(x(16)-4.75)^2), sqrt((x(15)-5.75)^2+(x(16)-5.0)^2),...
    sqrt((x(15)-3.0)^2+(x(16)-6.5)^2), sqrt((x(15)-7.25)^2+(x(16)-7.25)^2)]';
g(13)=x(1)*(x(13)-1.25)/g(1)+x(2)*(x(13)-8.75)/g(2)+x(3)*(x(13)-0.5)/g(3)+...
      x(4)*(x(13)-5.75)/g(4)+x(5)*(x(13)-3.0)/g(5)+x(6)*(x(13)-7.25)/g(6);
g(14)=x(1)*(x(14)-1.25)/g(1)+x(2)*(x(14)-0.75)/g(2)+x(3)*(x(14)-4.75)/g(3)+...
      x(4)*(x(14)-5.0)/g(4)+x(5)*(x(14)-6.5)/g(5)+x(6)*(x(14)-7.25)/g(6);
g(15)=x(7)*(x(15)-1.25)/g(7)+x(8)*(x(15)-8.75)/g(8)+x(9)*(x(15)-0.5)/g(9)+...
      x(10)*(x(15)-5.75)/g(10)+x(11)*(x(15)-3.0)/g(11)+x(12)*(x(15)-7.25)/g(12);
g(16)=x(7)*(x(16)-1.25)/g(7)+x(8)*(x(16)-0.75)/g(8)+x(9)*(x(16)-4.75)/g(9)+...
      x(10)*(x(16)-5.0)/g(10)+x(11)*(x(16)-6.5)/g(11)+x(12)*(x(16)-7.25)/g(12);

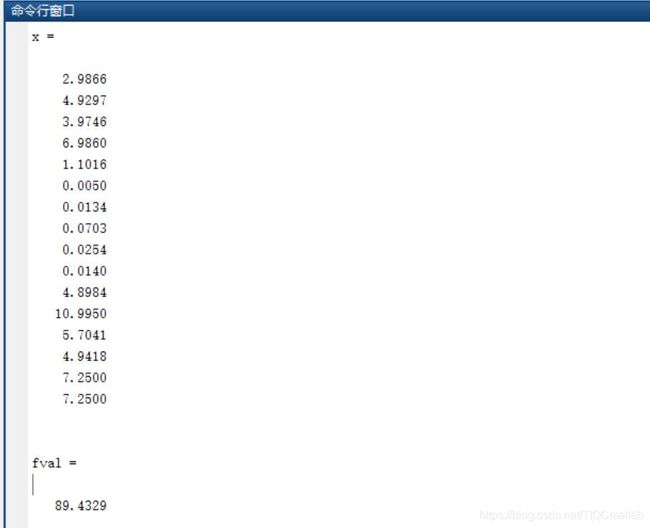
三、运行结果

四、备注

版本：2014a
完整代码或代写加QQ912100926