原链接:KMP算法详解|CloudWong
传统的字符串匹配模式(暴力循环)
子串的定位操作通常称作串的串的匹配模式,也就是在主串S中查找模式串(子串)T第一次出现的位置。如比较以下两个串:
主串S:ABCDABX
子串T:ABX
我们可以通过暴力循环的方式依次的比较S[i]和T[j],若匹配失败,则子串向前移位1步,重新开始匹配,直至匹配完成。
主串S:ABCDABX
子串T: ABX(匹配成功)
传统的暴力循环代码如下:
int index(String S,String T){
int i,j;
i = j = 0;
while(i StrLength(T)) return i - StrLength(T) + 1; //返回定位
return 0; //匹配失败
}
这种传统的模式匹配方式最坏的情况下需要循环mxn次,时间复杂度为O(mxn),因为主串中可能存在多个和模式串“部分匹配”的子串,因此指针多次回溯,效率极低。
KMP算法的匹配过程
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。用以下例子说明:
- 主串:abcababca...(假设主串很长,我们就先看前9位)
- 子串:abcabx
按照传统的匹配模式的过程就应该如下:
传统的匹配模式,就应该是按照上面的方式一步一步的匹配下来,一旦匹配失败,主串指针i就要回溯,效率非常低!而KMP算法的匹配过程只需要两步:
为什么一下次就可以跳过中间的比较来到这一步呢,下面就来探究KMP算法的匹配方式。
先来对比一下传统的匹配模式,可以发现主串的指针i值的变化:
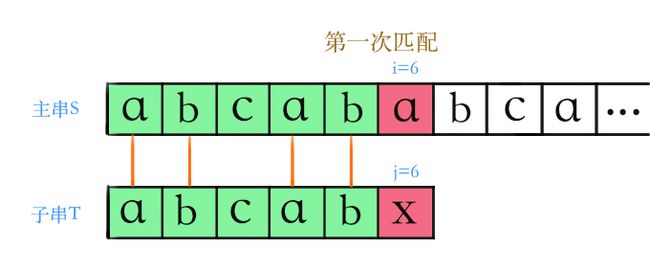
第一次遍历到了i=6,匹配失败;
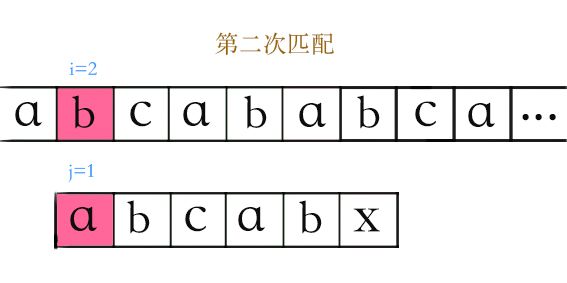
第二次遍历到了i=2,匹配失败;
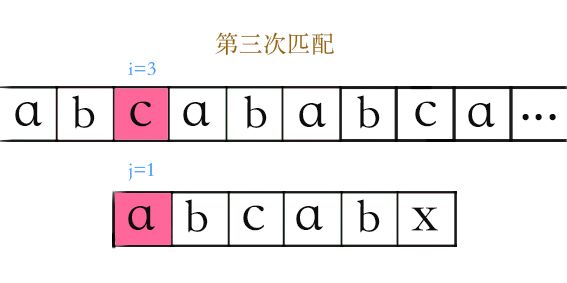
第三次遍历到了i=3,匹配失败;
第四次遍历到了i=4,匹配失败;
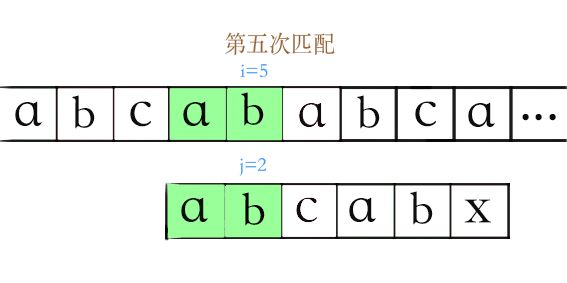
第五次遍历到了i=5,匹配失败;
直到第五次i值终于又回到了i=6。
i值的变化情况:6->1->2->3->4->5->6
在传统的匹配算法中,可以发现i值是不断回溯的。
反观KMP算法,只需对主串一次遍历,i值不会回溯,即遍历过程中i值是不会变小的。
那么既然KMP算法的i值遍历只需一次,那么就要考虑j是如何变化的了,为什么第一次匹配失败后j可以从j=3开始匹配,而不像传统遍历算法那样每当匹配失败就要从j=1重新开始匹配。
再看看一开始对KMP算法的定义:KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
划重点:利用匹配失败后的信息。什么是匹配失败后得到的信息呢?
于是回到刚刚的第一次匹配,看看能从这次失败的匹配中得到什么信息。
因为S[1...5] = T[1…5] 所以有 S[1,2] = T[1,2] S[4,5] = T[4,5]
又因为子串T有 T[1,2] = T[4,5],所以S[4,5] = T[1,2]
那下一次滑动到直接让S[4,5] = T[1,2],然后继续比较下一个元素就行啦。
这是简化模型第一次匹配的情况,根据传统的匹配算法,当匹配失败时模式串T移动一格,和S串比较。但是由于绿色部分在第一次匹配的时候发现了额外的信息:
就像刚刚那个例子,T[1,2] = S[4,5],都这样了,难道T还需要一格格的移动吗,直接滑过去就行啦。
这就是KMP算法的匹配过程。
如何确定模式串的滑动区间
知道了KMP算法的匹配过程,接下来就要考虑计算机是如何知道匹配失败时,指针j下一次指向的位置。由于KMP算法中指针i是不减的,因此j的指向位置只与模式串本身的结构有关。j的滑动位置的信息存放在next数组中。当匹配失败,就可以通过查询next数组的值得到下一次j滑动的位置。
next数组存放的是模式串的移位信息,具体就是模式串的部分匹配值,next数组大小与模式串T等长。
部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
下面是模式串T:a b c d a b c a | next数组的推导过程
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0
T[j]≠T[j] i++ next[i] = 0
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0
T[j]≠T[j] i++ next[i] = 0
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0 0
T[j]≠T[j] i++ next[i] = 0
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0 0 1
T[j]=T[j] i++ j++ next[i] = j+1
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0 0 1 2
T[j]=T[j] i++ j++ next[i] = j+1
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0 0 1 2 3
T[j]=T[j] i++ j++ next[i] = j+1
j i
模式串:a b c d a b c a
串下标:0 1 2 3 4 5 6 7
next :0 0 0 0 1 2 3
T[j]≠T[j] j = next[j-1]
j i
模式串:a b c d a b c a
j :0 1 2 3 4 5 6 7
next :0 0 0 0 1 2 3 1
T[j]=T[j] next[i] = j+1
最后得到 next[] = {0,0,0,0,1,2,3,1}
C语言的next数组实现如下:
void get_next(String T,int next[]){
int j = 0;
int i = 1;
next[0] = 0;
while(i有了next数组,我们就可以知道每当KMP匹配过程中,一旦匹配失败,我们就令指针 j = next[j-1] ,然后继续与S[i]比较。
KMP完整算法如下:
int KMP(String S,String T){
int length_S = StrLength(S);
int length_T = StrLength(T);
int next[length_T];
get_next(T,next);
int i = 0;
int j = 0;
while(j文章参考
字符串匹配的KMP算法
详解KMP算法
CODE
《大话数据结构》
《数据结构》—严蔚敏