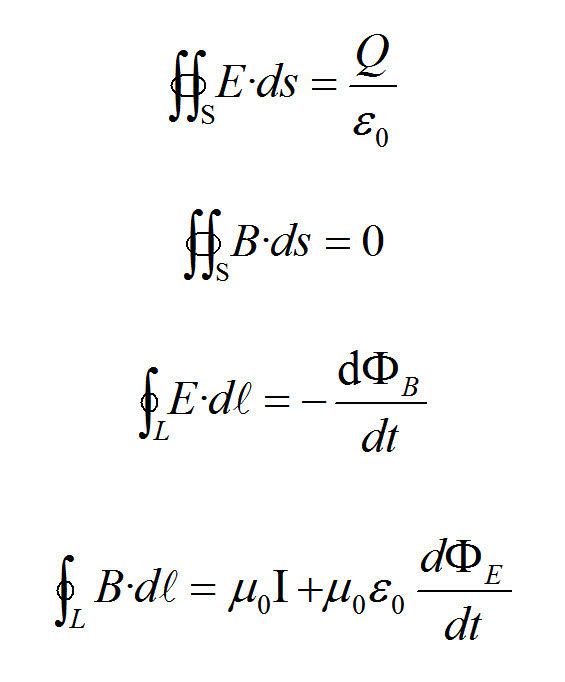有源电场与无源磁场与麦克斯韦方程

麦克斯韦方程由4个式子组成，其中2个关于电场、2个关于磁场，一起反映了空间某区域的E、B、q、I之间的关系。电荷产生电场，电流产生磁场。电荷和电流对电场和磁场干的事情是不一样的：电荷的作用是给电场贡献一些散度，而电流的作用是给磁场贡献一些旋度。然而变化的电磁场对对方干的事情是一样的，都是给对方贡献一些旋度。

麦克斯韦提出的涡旋电场和位移电流假说的核心思想是：
变化的磁场可以激发涡旋电场，
变化的电场可以激发涡旋磁场；
电场和磁场不是彼此孤立的，
它们相互联系、相互激发组成一个统一的电磁场
（也是电磁波的形成原理）。

据法拉第感应定律，变化的磁场会生成电场；根据麦克斯韦-安培定律，变化的电场生又成了磁场，正是这不停的循环使得电磁波能够自我传播？？如图9-10所示。

图9-10 电磁波

麦克斯韦提出：电可以变成磁，磁可以变成电，电和磁的这种相互转化和震荡不就是一种波吗？电磁场的振荡是周期存在的，这种振荡叫电磁波，一旦发出就会通过空间向外传播。但更神奇的是，当他用方程计算电磁波的传播速度时，结果接近300000公里/秒，恰与光的传播速度一致。这显然不只是个巧合。

电磁扰动就是光，光在本质上不过是电场和磁场的扰动。

麦克斯韦用对称的数学公式4个描述电磁关系。麦克斯韦方程组乃是由四个方程共同组成的：

1. 高斯定律：该定律描述静电场与空间中电荷分布的关系。电场线开始于正电荷，凡是有正电荷的地方，必有电力线发出；终止于负电荷，凡是有负电荷的地方，必有电力线会聚。计算穿过某给定闭曲面的电场线数量，即其电通量，可以得知包含在这闭曲面内的总电荷。更详细地说，这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。静电场是有源场；高斯定理是从库仑定律直接导出的，它完全依赖于电荷间作用力的二次方反比律。把高斯定理应用于处在静电平衡条件下的金属导体，就得到导体内部无净电荷的结论，因而测定导体内部是否有净电荷是检验库仑定律的重要方法。对于某些对称分布的电场,如均匀带电球的电场,无限大均匀带电面的电场以及无限长均匀带电圆柱的电场，可直接用高斯定理计算它们的电场强度。电位移对任一面积的能量为电通量，因而电位移亦称电通密度。
2. 高斯磁定律：该定律表明，磁单极子实际上并不存在。所以，没有孤立磁荷，磁场线没有初始点，也没有终止点，所以通过任何闭合面的磁通量必等于零。磁场线会形成循环或延伸至无穷远。换句话说，进入任何区域的磁场线，必需从那区域离开。这个规律类似于电场中的高斯定理，因此也称为高斯定理。以术语来说，通过任意闭曲面的磁通量等于零，或者，磁场是一个无源场。
3. 法拉第感应定律：该定律描述时变磁场怎样感应出电场。电磁感应是制造许多发电机的理论基础。例如，一块旋转的条形磁铁会产生时变磁场，这又接下来会生成电场，使得邻近的闭合电路因而感应出电流。
4. 麦克斯韦-安培定律：该定律阐明，磁场可以用两种方法生成：一种是靠传导电流（原本的安培定律），另一种是靠时变电场，或称位移电流（麦克斯韦修正项）。

麦克斯韦方程组微积分形式：

以总电荷和总电流为源头的表述 :
名称	微分形式	微分形式解释	积分形式
高斯定律		电场E的散度，等于在该点的电荷密度ρ（乘上系数1/ε0）；		计算穿过某给定闭曲面的电场线数量，即其电通量，可以得知包含在这闭曲面内的总电荷。描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
高斯磁定律		磁场B的散度，等于0； 磁感强度的散度处处等于零 （磁通连续性原理） 。		通过任何闭合面的磁通量必等于零。
法拉第感应定律		电场E的旋度，等于在该点的磁场B的变化率（乘上系数-1）；		描述时变磁场怎样感应出电场。电场E沿闭合回线L 的积分，等于穿过该闭合回线磁通随时间的变化率。简化形式：绕组接线端感应电压，为磁链。
麦克斯韦-安培定律 （全电流定律）		磁场B的旋度，等于在该点的电流密度J（乘上系数μ0），加上在该点的电场E的变化率（乘上系数μ0ε0）。		磁场可以用两种方法生成：一种是靠传导电流（原本的安培定律），另一种是靠时变电场，或称位移电流（麦克斯韦修正项）。

以自由电荷和自由电流为源头的表述 :
名称	微分形式		积分形式
高斯定律
高斯磁定律
法拉第感应定律
麦克斯韦-安培定律				磁场与产生磁场的电流之间的关系：磁场强度H的切线分量沿闭合回路C的线积分等于通过与该回路关联的任何表面S的总电流。

 

符号	物理意义	国际单位
	电场强度	V ／ m ， N ／ C
	磁场强度	A ／ m
	电位移	C ／ m 2 ， N ／ V · m
	磁感应强度 磁通密度？？	T ， Wb/m 2 ， V · s/m2
	散度 算符	／ m
	旋度 算符
	对于时间的偏导数	／ s
	曲面积分的运算曲面	m 2
	路径积分的运算路径	m
	微小面元素矢量	m 2
	微小线元素矢量	m
	电常数	F ／ m
	磁常数	H ／ m ， N ／ A 2
	自由电荷密度	C ／ m 3
	总电荷密度	C ／ m 3
	在闭曲面   里面的 自由电荷	C
	在闭曲面   里面的总 电荷	C
	自由电流密度	A ／ m 2
	总电流密度	A ／ m 2
	穿过闭路径   所包围的曲面的 自由电流	A
	穿过闭路径   所包围的曲面的总 电流	A
	穿过闭路径   所包围的曲面   的 磁通量	T·m 2 ， V·s ， Wb
	穿过闭路径   所包围的曲面   的 电通量	J·m/C
	穿过闭路径   所包围的曲面   的电位移 通量	C

国际单位制 电磁学 单位
名称	符号	量纲	物理量
安培	A	A	电流
库仑	C	A·s	电荷量
伏特	V	J/C = kg·m 2 ·s −3 ·A −1	电压
欧姆	Ω	V/A = kg·m 2 ·s −3 ·A −2	电阻 、 阻抗 、 电抗
欧姆 米	Ω·m	kg·m 3 ·s −3 ·A −2	电阻率
瓦特	W	V·A = kg·m 2 ·s −3	功率
法拉	F	C/V = kg −1 ·m −2 ·A 2 ·s 4	电容
法拉 每 米	F/m	kg −1 ·m −3 ·A 2 ·s 4	电容率
倒 法拉	F −1	kg 1 ·m 2 ·A −2 ·s −4	倒电容
西门子	S	Ω −1  = kg −1 ·m −2 ·s 3 ·A 2	电导 ,  导纳 ,  电纳
西门子 每 米	S/m	kg −1 ·m −3 ·s 3 ·A 2	电导率
韦伯	Wb	V·s = kg·m 2 ·s −2 ·A −1	磁通量
特斯拉	T	Wb/m 2  = kg·s −2 ·A −1	磁通量密度、磁感应强度
安培 每 米	A/m	m −1 ·A	磁场强度
安培 每 韦伯	A/Wb	kg −1 ·m −2 ·s 2 ·A 2	磁阻
亨利	H	Wb/A = V·s/A = kg·m 2 ·s −2 ·A −2	自感
亨利 每 米	H/m	kg·m·s −2 ·A −2	磁导率
(无量纲)	χ	-	磁化率

 

◆ （11-4）

 

我们可以看出，

上图微分别表示为：

（1）

（2）电场强度的旋度（法拉第电磁感应定律）等于该点处磁感强度变化率的负值；

 

 

第四个式子是麦克斯韦将安培环路定理推广后的全电流定律。

其中，左边L、B、dl物理意义同上，分别是路径积分的运算路径、磁场、闭合曲线上的微分。右边是磁常数，Ι是穿过闭合路径L所包围的曲面的总电流，是绝对介电常数，是穿过闭合路径L所包围的曲面的电通量（计算如式一左边），表示电通量对时间t的导数，也即变化率。

它表示，磁场B在闭合曲线上的环量，等于该曲线包围的曲面S里的电流Ι（系数是磁常数），加上电场E在该曲线包围的曲面S上的通量的变化率（系数是）。

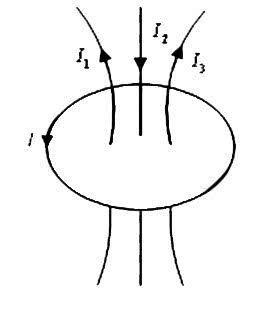
原安培环路定律是一系列电磁定律，它总结了电流在电磁场中的运动规律，如图9-8所示。安培定律表明，电流可以激发磁场，但它只限用于稳恒磁场。

图9-8 安培环路定理：在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。这个结论称为安培环路定理（Ampere circuital theorem）。安培环路定理可以由毕奥－萨伐尔定律导出。它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。只适用于静态磁场。

因此，麦克斯韦将安培环路定理推广，提出一种“位移电流”假设，得出一般形式下的安培环路定律，揭示出磁场可以由传导电流激发，也可以由变化电场的位移电流所激发。

传导电流和位移电流合在一起，称为全电流，这就是麦克斯韦—安培定律。

这一定律反映了电场是如何产生磁场的，即描述了变化的电场激发磁场的规律。这一规律和法拉第电磁感应定律相反：当电场随时间变化时，会诱导一个围绕电场的磁场。

 

相关物理公式

安培定律也就是电流产生磁场的定律。描述了“一个”来源（电流）产生的“场”。

库仑定律描述了“两个”微小来源（电荷）之间的“力”。

电磁学中也有磁场版本的库仑定律，描述了两个微小电流之间的力，叫做毕奥-萨伐尔定律Biot-Savart Law；反之，也有电场版本的安培定律，描述了一个电荷产生的磁场，叫做高斯定律Gauss's Law。

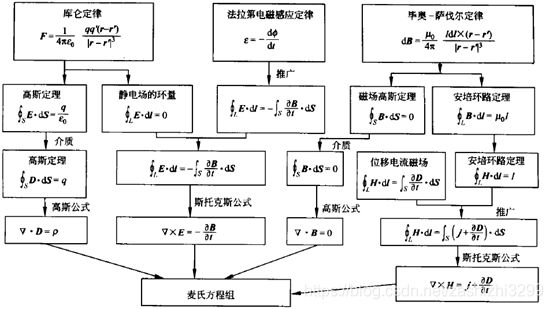
这四个定律之间有如下关系：

数学上可以证明，库仑定律（毕奥-萨伐尔定律）和高斯定律（安培定律）在静电学（静磁学）中是完全等价的。也就是说，我们可以任意假设一个定律，从而推导出另一个定律。

法拉第发现了电磁感应，也就是说变化的磁场是可以产生电场的，这就是法拉第定律Faraday's Law。

类似地，麦克斯韦发现安培定律的描述并不完善，除了电流之外，变化的电场也可以产生磁场，这被称为安培-麦克斯韦定律Ampere-Maxwell Law。

推导过程：

 

 

数学基础：散度、旋度、梯度

麦克斯韦方程组有微分和积分2种形式。

积分形式繁琐，原因有二：一方面，积分是很难算的，虽然每一个方程的左右两边都必然相等，但随便给你一个场和一个曲面/曲线，想把左侧的积分算出来极为困难；另一方面，也正因为如此，我们尽管有可以描述电磁场的方程，但给定一个特定的来源（比如天线中一个来回摇摆的电荷），我们想算出具体的E和B也是极为困难，因为我们只知道E和B在某个特殊曲面/曲线上的积分。

微分形式的好处：首先，计算一个给定向量场的微分（散度和旋度）是很简单的，只要使用之前提到过的∇·和∇×算符就好，而这两个算符都有一套固定的算法；其次，散度和旋度代表着一个向量场的两种不同的自由度，有着非常直接的几何意义，从这两个量中恢复出向量场也是比较直观的过程。

散度divergence，顾名思义，是指一个向量场发散的程度。一个向量场F的散度是一个标量场（向量场的每一点有一个自己的散度），写作∇·F（这个写法也很直白，因为点乘就是标量）。如果一个点的散度为正，那么在这一点上F有向外发散的趋势；如果为负，那么在这一点上F有向内收敛的趋势。

旋度curl则指一个向量场旋转的程度。一个向量场F的旋度是一个向量场（向量场的每一点有一个自己的旋度，而且是一个向量；这是因为旋转的方向需要标明出来），写作∇×F（这个写法也很直白，因为叉乘就是向量）。如果一个点的旋度不为0，那么在这一点上F有漩涡的趋势，而这个旋度的方向表明了旋转的方向。

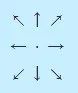
举些两个向量场，第一个向量场往外发散，但完全没有旋转扭曲的趋势；第二个向量场形成了一个标准的漩涡，但没有任何箭头在往外或往里指，没有发散或收敛的趋势。

散度不为0、但旋度为0的向量场：旋度不为0、但散度为0的向量场：

 

                                          

 

只要知道一个向量场的散度和旋度，我们就可以唯一确定这个向量场本身。

麦克斯韦方程组的微分形式，就是要描述电磁场的散度和旋度。我前边说到，微分形式和积分形式是完全等价的，我很也可以很轻松地从一个形式推导出另一个形式，用的是高斯定理（不要和高斯定律混淆、又叫散度定理）和斯托克斯定理。

高斯定理Gauss's Theorem：一个向量场F在闭合曲面∂V上的通量，等于该曲面包裹住的体积V里的F全部的散度（F的散度的体积积分）。这是可以想象的，毕竟通量就是在计算有多少场从这个闭合曲面里发散出去了，也就是总共的散度（散度的积分）。

斯托克斯定理Stokes' Theorem：一个向量场F在闭合曲线∂S上的环量，等于该曲线环住的曲面S上的F全部的旋度（F的旋度的曲面积分）。这也是可以想象的，毕竟环量就是在计算有多少场和这个环方向一样（有多少场在沿着这个环旋转），也就是总共的旋度（旋度的积分）。

总结如下表：

在保守力场的这样一个式子：F=-∇V。这里F是个向量场，V是个标量场。我们看到，这个神奇的倒三角不但可以表示散度（把向量变成标量）和旋度（把向量变成向量），还可以这样把一个标量场变成一个向量场！数学上这个倒三角叫Nabla算符，而∇V叫做一个标量场V的梯度。梯度gradient就是一个标量场变化的程度。

总结一下我们见到的三种向量微分：

于是，从F=-∇V这个公式我们看到，保守力场（比如引力场）可以表示为某个标量场（比如引力势能）的梯度。之前说过， 保守力场的环量/旋度一定为0。这也就是说，梯度的旋度一定为0。这是可以想象的，梯度指的是上坡的方向；而如果它有旋度，就意味着它们的指向可以形成的 一个环，在这个环上可以一直上坡。这就像彭罗斯楼梯，是不可能的情形。

还有一个类似的定理，是说旋度的散度一定为0。我们也来想一下几何上这意味着什么。如果旋度有散度，就意味着在某个球上散度都在往球外指，也就意味着在球上每个点这个场都是逆时针旋转的。想想也知道这是不可能的，所以我们得到了两个重要的结论：

1、任意标量场V的梯度∇V都是没有旋度的，也就是∇×(∇V)=0；

2、任意向量场F的旋度∇×F都是没有散度的，也就是∇·(∇×F)=0。

这些“X度”都可以认为是场的一种微分，那么这些“X度的X度”就可以认为是二次导数了。我们看到，有两种二次导数都自动为0，不必我们深究。还有一种二次导数也很有名，也就是梯度的散度，它甚至有了一个专门的花哨的名字，叫“拉普拉斯算符”Laplacian。

 

 

库仑定律：

毕奥-萨伐尔定律：

 

Nabla算符：

 

梯度：

 

散度：

 

旋度：

 

高斯定理：

 

斯托克斯定理：

 

真空中的电磁波：

 

 

 

 

 

 

参考文献：

1、电磁学-赵凯华

2、[理论物理 第三册] 吴大猷 - 电磁学 (1983, 科学出版社)

3、麦克斯韦方程组（彩图完美解释版) - exce4 - 博客园  https://www.cnblogs.com/bluespot/p/3951184.html

4、【射频笔记4】想搞清楚“麦克斯韦方程组”，你得先懂这个。 散度、旋度、梯度度 http://www.360doc.com/content/16/0610/17/908538_566543693.shtml

5、麦克斯韦方程组：史上最伟大的公式，没有之一，都了解一下  https://new.qq.com/omn/20190101/20190101A10TMZ.html

6、麦克斯韦方程组浅析 - 百度文库  https://wenku.baidu.com/view/1ac761c7dd88d0d233d46a7a.html

7、维基百科 ： http://zh.wikipedia.org/zh-cn/ 麦克斯韦方程组

8、电机学，（美）A.E.Fitzgerald，刘新正译. 电子工业出版社

9、史上最透彻的讲解：麦克斯韦方程组 https://mp.weixin.qq.com/s/7Sgtg9GvkMedivOCsJ6PgQ

10、

11、

12、

13、

14、