matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结
1、基本概念
| 点集 | 区间 | 领域 | ||
|---|---|---|---|---|
| 一维 | 直线 | 实数集 | 线段(端点) | (不含端点) |
| 二维 | 平面 | 实平面 | 平面区域(边界) | (不含边界) |
| 三维 | 空间 | 实空间 | 曲面(边界)&体(表面) | (不含边界&表面) |
点和点集的关系
| 内点 | 外点 | 边界点 |
|---|---|---|
| 点集E内 | 点集E外 | 点集E边界上 |
| 存在领域属于E | 存在领域与E交集为空 | 任意领域与E、CUE皆有交集 |
重要的平面点集
| 名称 | 含义 |
|---|---|
| 开集 | 没边界点 |
| 闭集 | 包含内点和边界点 |
| 连通集 | 任意两点连连看 |
| 开区域 | 连通开集 |
| 闭区域 | 连通闭集 |
| 有界集 | 能找着一个确定的最大半径 |
e.g.
{(x,y)|1
{(x,y)|x²>1}无界、开集、不连通
2、多元函数
概念(n元函数):
任意(x,y)属于D属于R^n, 存在唯一u属于R使得f(a,b,c,……,n)=u
二重极限(以二元为例,可推广至n元):
设f(x,y)在P0(x0,y0)极限为A,存在一个半径δ,使f(x,y)所有点P(x,y)都在P0的这个半径的去心邻域里,从而使得f(x,y)与A的差的绝对值小于任意一个极小正值(即无穷小)。
重点:
证明:找到那个半径0
证反:P趋于P0,方向任意&&路径任意(无穷多≠任意)
e.g.
| 性质 | 备注 |
|---|---|
| 多元初等函数在定义区域内连续 | 定义区域包含在定义域内;极限值=函数值 |
| 有界性定理 | |
| 最值定理 | 值为一,取值点不唯一 |
| 介值定理 | 能取到最值间任一函数值 |
3、偏导数
偏增量(在x0处关于x):Δxz=f(x0+Δx,y0)-f(x0,y0)
偏导数(在x0处关于x):当Δx趋于0时(Δxz/Δx)的极限
求偏导实质上,就是将其他变量视作常数对指定自变量求导。
有时候可以通过先将其他自变量数值代入以简化计算。
巧妙运用轮换对称性简化计算。
导数拆开表示微商;偏导数是一个整体符号,不能拆分,不能抵消。
求分段点、不连续点处的偏导数要用定义。
几何意义:
导数:关于自变量x变化的切线斜率
二元函数的偏导数:在曲面中,由其中一自变量y0确定出一个平面,平面与曲面交线关于x变化的切线斜率
| 一元函数 | 导数存在→连续→有极限 |
| 多元函数 | 偏导数存在 不能推 连续、有极限;连续→有极限 |
偏导数存在,函数不一定连续
偏导数存在→一元函数极限定义
连续性→二元函数极限定义
函数连续,偏少数不一定存在
e.g.上半圆锥,对顶点处的偏导不存在
高阶偏导数
若连续,则混合偏导数与对自变量求偏导数的先后次序无关
偏导数求不定积分时,需加上一关于其他自变量的函数项(相当于一元函数的C)
4、全微分
偏增量(关于x):Δxz=f(x+Δx,y)-f(x,y)
全增量:Δz=f(x+Δx,y+Δy)-f(x,y)=AΔx+BΔy+o(ρ)
ρ为两点间距
全微分:dz=df=AΔx+BΔy=fxdx+fydy
一元函数
多元函数
判断二元函数全微分存在
应用:近似计算
5、多元复合函数求导
链式法则
连线相乘,分线相加,一元全导,多元偏导
抽象函数求偏导
全微分形式不变性
(无论u、v是自变量还是中间变量,结果形式相同)
6.隐函数求导
一个方程的情形
隐函数求导公式[公式法]
F(x,y):
F(x,y,z):
全微分形式不变性[微分法]
对方程两边同时求微分,
化简为以下形式:
得到du、dv前系数即为一阶偏导
[直接求导法]
就字面上的意思,方程两边同时对某一变量求偏导,然后移项化简得到偏导
由方程组确定的隐函数
设F(x,y,u,v),G(x,y,u,v)满足
①在点P(x0,y0,u0,v0)的某个领域内具有连续偏导数
②F(x0,y0,u0,v0)=0,G(x0,y0,u0,v0)=0
③
推导
F(x,y,u(x,y),v(x,y))=0
G(x,y,u(x,y),v(x,y))=0
两式同时对x求偏导
对y求偏导同理
方程个数=因变量个数=确定的函数个数
总变量个数-因变量个数=自变量个数
解题步骤
①对确定函数的方程两边同时对自变量求导(多个自变量则分别求偏导)
②通过克莱默法则或其他代数运算得到结果
③如果题目还有其他要求,如求二阶导,自个继续求就行
7.多元函数微分学的几何应用
线
x=x(t)
y=y(t)
z=z(t)
参数曲线的切线与法平面
切向量:(x'(t),y'(t),z'(t))
切线:(点向式方程)
法平面:(点法式方程)
两曲面的交线的切线与法平面
方程组两边对x求导,解出dy/dx,dz/dx,之后与前面同理
面
F(x,y,z)=0
F(x(t),y(t),z(t))=0
曲面的切平面与法线
法向量:
(F_x,F_y,F_z)
法线:(点向式方程)
切平面:(点法式方程)
特殊的当z=f(x,y)时
令F(x,y,z)=f(x,y)-z=0
其他如上同理
法向量的方向余弦
一次项 x→x+x0, y→y+y0
平方项 x^2→xx0, y^2→yy0
交叉项 2xy→x0y+xy0
8.方向导数与梯度
偏导数:fx、fy表示f(x,y)沿x、y轴方向的变化率
方向导数:fl表示f(x,y)沿方向向量l的变化率
方向导数是单侧导数,偏导数是双侧导数
z=f(x,y)沿各个方向的方向导数存在,偏导数不一定存在
z=f(x,y)P点沿任意方向的方向导数存在,在P点不一定连续
梯度
几何意义:法向量低指高
二元函数:
以一座山在一象限以正海拔为z轴正方向建立空间直角坐标系,取低海拔与高海拔两条闭合等高线在xoy面投影,每条等高线为一条等值线,等高线边缘一点梯度由外指内,z的低值指向高值,即由低海拔指向高海拔酱紫
同理,一个谷则是等高线由内指外,但还是z的低值指向高值,即由低海拔指向高海拔
三元函数:
这时候整个山的表面是一个等值面,山体外边是高值,山体内部是低值,低指高就是内指外
谷的话,也就是说凹面,谷表面是一个等值面,谷内部在等值面上方是高值,也就是外指内
9.多元函数的极值
一元函数的极值
定义理解:有个点x0,在法则f下算出来的值比两边都大(都小),称极大值(极小值)
充分条件
导数由正变负,在该点取极大值;负变正,极小值
一阶导为0,二阶导小于零,在该点取极大值;大于零,取极小值
必要条件
函数y=f(x)在点可导,且在该点取得极值,则
极值是局部概念
极值点必须是定义域的内点
定义可推广到多元函数
多元函数的极值
定义理解:有个点(x0,y0),在法则f下算出来的值比周围一圈都大(都小),称极大值(极小值)
驻点:使偏导数同时为0的点
偏导数存在的极值点一定是驻点
驻点不一定是极值点
可能的极值点:驻点、不可导点
必要条件
函数z=f(x,y)在点(x0,y0)存在偏导数,且在该点取得极值,则
充分条件
AC-B^2>0 无极值
几何意义
最值
方法:全部可能最值点求出来,再直接求出其值比较(无需判断最大最小值点)
条件极值
对自变量除定义域限制外还有其他条件限制
[代入法] 显式直接代换消元
[拉格朗日乘数法] 隐式难显化
10.常见题型
1.求多元函数的定义域或表达式
2.求多元函数的极限或判断极限不存在
3.求函数在一点的偏导数、全微分 多元分段函数在一-点的偏导数、全微分
4.偏导函数与全微分的计算
5.复合函数与隐函数的求导计算
6.求偏导数(包括高阶导数)及微分
①显函数及抽象函数
②多元复合函数
③多元隐函数
④交织综合函数
7.偏导数的几何应用(求空间曲线的切线及空间曲面的切平面)
8.求极值与最值
9.偏导数的逆问题
(
ps:
我有尽力在写了,但无奈微信不支持markdown只好把部分内容截图放上来,应该不会过分影响观感。
如果有什么问题请在评论中指出,我会及时改正的。
大家高数加油!
)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第1张图片](http://img.e-com-net.com/image/info8/9f2a7507003f4a33916618cf6b2f7281.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第2张图片](http://img.e-com-net.com/image/info8/d5ddd4c5de124fdb9f485fe8e7f11ba2.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第3张图片](http://img.e-com-net.com/image/info8/7c63766b2fd24a618e351b6e0efb4640.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第4张图片](http://img.e-com-net.com/image/info8/77deaaba4aa24069a3bb436b07e55be0.jpg)

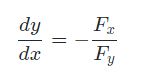
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第5张图片](http://img.e-com-net.com/image/info8/3243bc49456b46bd9090c04980571d2d.jpg)
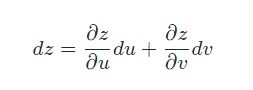

![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第6张图片](http://img.e-com-net.com/image/info8/bce4ccaced5e4f9fa90f37d0b09de2d7.jpg)



![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第7张图片](http://img.e-com-net.com/image/info8/f7696ea99fb5436498c02e5d2154aa8e.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第8张图片](http://img.e-com-net.com/image/info8/1b9150d4d6174d10a9583ef156edd6d7.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第9张图片](http://img.e-com-net.com/image/info8/6ee7489561cd4a22a867fce04c6f4735.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第10张图片](http://img.e-com-net.com/image/info8/59fb15321b52421e9fe29ba6594228e5.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第11张图片](http://img.e-com-net.com/image/info8/82f3605106ce4638ab5de6fc52a35de8.jpg)
![matlab求二元函数极值算法_[小白头秃]多元函数基本概念总结_第12张图片](http://img.e-com-net.com/image/info8/7cf5e3f8dd1d4e7095e0e39e5d964271.jpg)