吴恩达机器学习课后作业——逻辑回归(Python实现)
1.写在前面
吴恩达机器学习的课后作业及数据可以在coursera平台上进行下载,只要注册一下就可以添加课程了。所以这里就不写题目和数据了,有需要的小伙伴自行去下载就可以了。
作业及数据下载网址:吴恩达机器学习课程
2.逻辑回归实现
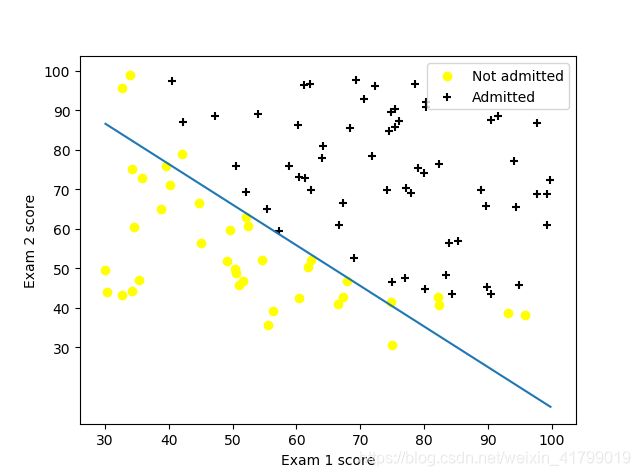
逻辑回归的作业主要包含两个任务:对决策边界进行可视化以及进行预测。下面附上代码,有详细的注释,这里就不一一解释了。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
from collections import OrderedDict
#用于导入数据的函数
def inputData():
#从txt文件中导入数据,注意最好标明数据的类型
data = pd.read_csv('MachineLearning\\machine-learning-ex2\\machine-learning-ex2\\ex2\\ex2data1.txt'
,dtype={
0:float,1:float,2:int})
#插入一列全为1的列
data.insert(0,"one",[1 for i in range(0,data.shape[0])])
#分别取出X和y
X=data.iloc[:,0:3].values
y=data.iloc[:,3].values
y=y.reshape(y.shape[0],1)
return X,y
#用于最开始进行数据可视化的函数
def showData(X,y):
#分开考虑真实值y是1和0的行,分别绘制散点,并注意使用不同的label和marker
for i in range(0,X.shape[0]):
if(y[i,0]==1):
plt.scatter(X[i,1],X[i,2],marker='+',c='black',label='Admitted')
elif(y[i,0]==0):
plt.scatter(X[i,1],X[i,2],marker='o',c='yellow',label='Not admitted')
#设置坐标轴和图例
plt.xticks(np.arange(30,110,10))
plt.yticks(np.arange(30,110,10))
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
#因为上面绘制的散点不做处理的话,会有很多重复标签
#因此这里导入一个集合类消除重复的标签
handles, labels = plt.gca().get_legend_handles_labels() #获得标签
by_label = OrderedDict(zip(labels, handles)) #通过集合来删除重复的标签
plt.legend(by_label.values(), by_label.keys()) #显示图例
plt.show()
#定义sigmoid函数
def sigmoid(z):
return 1/(1+np.exp(-z))
#计算代价值的函数
def showCostsJ(X,y,theta,m):
#根据吴恩达老师上课讲的公式进行书写
#注意式子中加了1e-6次方是为了扩大精度,防止出现除0的警告
costsJ = ((y*np.log(sigmoid(X@theta)+ 1e-6))+((1-y)*np.log(1-sigmoid(X@theta)+ 1e-6))).sum()/(-m)
return costsJ
#用于进行梯度下降的函数
def gradientDescent(X,y,theta,m,alpha,iterations):
for i in range(0,iterations): #进行迭代
#根据吴恩达老师的公式,进行向量化的计算。
#注意下面第二行使用X.T@ys可以替代掉之前的同步更新方式,写起来更简洁
ys=sigmoid(X@theta)-y
theta=theta-alpha*(X.T@ys)/m
#以下完全根据吴恩达老师视频中进行编写代码,可以代替上面两行的代码
# temp0=theta[0][0]-alpha*(ys*(X[:,0].reshape(X.shape[0],1))).sum() #注意这里一定要将X[:,1]reshape成向量
# temp1=theta[1][0]-alpha*(ys*(X[:,1].reshape(X.shape[0],1))).sum()
# temp2=theta[2][0]-alpha*(ys*(X[:,2].reshape(X.shape[0],1))).sum()
# theta[0][0]=temp0 #进行同步更新θ0和θ1和θ2
# theta[1][0]=temp1
# theta[2][0]=temp2
return theta
#对决策边界进行可视化的函数
def evaluateLogisticRegression(X,y,theta):
#这里和上面进行数据可视化的函数步骤是一样的,就不重复阐述了
for i in range(0,X.shape[0]):
if(y[i,0]==1):
plt.scatter(X[i,1],X[i,2],marker='+',c='black',label='Admitted')
elif(y[i,0]==0):
plt.scatter(X[i,1],X[i,2],marker='o',c='yellow',label='Not admitted')
plt.xticks(np.arange(30,110,10))
plt.yticks(np.arange(30,110,10))
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')
handles, labels = plt.gca().get_legend_handles_labels()
by_label = OrderedDict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys())
minX=np.min(X[:,1]) #取得x1中的最小值
maxX=np.max(X[:,1]) #取得x1中的最大值
xx=np.linspace(minX,maxX,100) #创建等间距的数100个
yy=(theta[0][0]+theta[1][0]*xx)/(-theta[2][0]) #绘制决策边界
plt.plot(xx,yy)
plt.show()
#利用训练集数据判断准确率的函数
def judge(X,y,theta):
ys=sigmoid(X@theta) #根据假设函数计算预测值ys
yanswer=y-ys #使用真实值y-预测值ys
yanswer=np.abs(yanswer) #对yanswer取绝对值
print('accuary:',(yanswer<0.5).sum()/y.shape[0]*100,'%') #计算准确率并打印结果
X,y = inputData() #输入数据
theta=np.zeros((3,1)) #初始化theta数组
alpha=0.004 #设定alpha值
iterations=200000 #设定迭代次数
theta=gradientDescent(X,y,theta,X.shape[0],alpha,iterations) #进行梯度下降
judge(X,y,theta) #计算准确率
evaluateLogisticRegression(X,y,theta) #决策边界可视化
3.正则化逻辑回归
正则化逻辑回归的作业主要包含两个任务:进行数据映射、实现正则化的梯度下降,绘制决策边界以及进行预测。下面附上代码,有详细的注释,这里就不一一解释了。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
#用于导入数据的函数
def inputData():
#从txt文件中导入数据,注意最好标明数据的类型
data=pd.read_csv('MachineLearning\\machine-learning-ex2\\machine-learning-ex2\\ex2\\ex2data2.txt'
,dtype={
0:float,1:float,2:int})
#插入一列全为1的列
data.insert(0,"ones",np.ones((data.shape[0],1)))
#分别取出X和y
X=data.iloc[:,0:3]
X=X.values
y=data.iloc[:,3]
y=(y.values).reshape(y.shape[0],1)
return X,y
#用于最开始进行数据可视化的函数
def showData(X,y):
#分开考虑真实值y是1和0的行,分别绘制散点,并注意使用不同的label和marker
for i in range(0,X.shape[0]):
if(y[i][0]==1):
plt.scatter(X[i][1],X[i][2],marker="+",c='b',label='y=1')
else:
plt.scatter(X[i][1],X[i][2],marker='o',c='y',label='y=0')
#设置坐标轴和图例
plt.xticks(np.arange(-1,1.5,0.5))
plt.yticks(np.arange(-0.8,1.2,0.2))
plt.xlabel('Microchip Test 1')
plt.ylabel('Microchip Test 2')
#因为上面绘制的散点不做处理的话,会有很多重复标签
#因此这里导入一个集合类消除重复的标签
handles, labels = plt.gca().get_legend_handles_labels() #获得标签
by_label = OrderedDict(zip(labels, handles)) #通过集合来删除重复的标签
plt.legend(by_label.values(), by_label.keys()) #显示图例
plt.show()
#定义sigmoid函数
def sigmoid(z):
return 1/(1+np.exp(-z))
#计算代价值的函数
def computeCostsJ(X,y,theta,lamda,m):
#根据吴恩达老师上课讲的公式进行书写
hx=sigmoid(X@theta)
costsJ=-(np.sum(y*np.log(hx)+(1-y)*np.log(1-hx)))/m+lamda*np.sum(np.power(theta,2))/(2*m)
return costsJ
#进行特征映射
def featureMapping(x1,x2,level):
answer = {
} #定义一个字典
for i in range(1,level+1): #外层循环,映射的阶数
for j in range(0,i+1): #内存循环,x1的次数
answer['F{}{}'.format(i-j,j)]=np.power(x1,i-j)*np.power(x2,j) #形成字典中的key-value
answer = pd.DataFrame(answer) #转换为一个dataframe
answer.insert(0,"ones",np.ones((answer.shape[0],1))) #插入第一列全1
return answer.values
#进行梯度下降的函数
def gradientDescent(X,y,theta,alpha,iterations,m,lamda):
for i in range(0,iterations+1):
hx=sigmoid(X@theta)
temp0=theta[0][0]-alpha*np.sum(hx-y)/m #因为x0是不需要进行正则化的,因此需要单独计算
theta=theta-alpha*(X.T@(hx-y)+lamda*theta)/m #根据公式进行同步更新theta
theta[0][0]=temp0 #单独修改theta0
return theta
#利用训练集数据判断准确率的函数
def judge(X,y,theta):
ys=sigmoid(X@theta) #根据假设函数计算预测值ys
yanswer=y-ys #使用真实值y-预测值ys
yanswer=np.abs(yanswer) #对yanswer取绝对值
print('accuary',(yanswer<0.5).sum()/y.shape[0]*100,'%') #计算准确率并打印结果
#对决策边界进行可视化的函数
def evaluateLogisticRegression(X,y,theta):
#这里和上面进行数据可视化的函数步骤是一样的,就不重复阐述了
for i in range(0,X.shape[0]):
if(y[i][0]==1):
plt.scatter(X[i][1],X[i][2],marker="+",c='b',label='y=1')
else:
plt.scatter(X[i][1],X[i][2],marker='o',c='y',label='y=0')
plt.xticks(np.arange(-1,1.5,0.5))
plt.yticks(np.arange(-0.8,1.2,0.2))
plt.xlabel('Microchip Test 1')
plt.ylabel('Microchip Test 2')
handles, labels = plt.gca().get_legend_handles_labels()
by_label = OrderedDict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys())
#通过绘制等高线图来绘制决策边界
x=np.linspace(-1,1.5,250) #创建一个从-1到1.5的等间距的数
xx,yy = np.meshgrid(x,x) #形成一个250*250的网格,xx和yy分别对应x值和y值
#利用ravel()函数将xx和yy变成一个向量,也就是62500*1的向量
answerMapping=featureMapping(xx.ravel(),yy.ravel(),6) #进行特征映射
answer=answerMapping@theta #代入映射后的数据进行计算预测值
answer=answer.reshape(xx.shape) #将answer换成一样格式
plt.contour(xx,yy,answer,0) #绘制等高线图,0代表绘制第一条等高线
plt.show()
X,y = inputData() #导入数据
theta=np.zeros((28,1)) #初始化theta数组
iterations=200000 #定义迭代次数
alpha=0.001 #定义alpha值
lamda=100 #定义lamda
mappingX = featureMapping(X[:,1],X[:,2],6) #进行特征映射
theta=gradientDescent(mappingX,y,theta,alpha,iterations,X.shape[0],lamda) #进行正则化的梯度下降
judge(mappingX,y,theta) #计算预测的准确率
evaluateLogisticRegression(X,y,theta) #绘制决策边界