2021年第十二届蓝桥杯第一场c/c++ b组

解题思路

32位=4B
1MB=1024KB=1024B
故答案为: 25610241024/4=67108864

解题思路
送分题，但要注意题目中的陷阱，有3张卡片的时候，是能拼出10不能拼出11.

#include 
#include 
//答案3181
int main()
{
     
    int i;
    int flag=1;
    int a[10];
    for(i=0;i<10;i++)
        a[i]=2021;
    for(i=1;;i++)
    {
     
        int t=i;
        int temp;
        while(t!=0)
        {
     
            temp=t%10;
            if(a[temp]<=0)
            {
     
                flag=0;
                i--;   //这个数已经拼不出来了
                break;
            }
            a[temp]--;
            t=t/10;
        }
        if(!flag)
            break;
    }
    printf("%d",i);
    return 0;
}

答案:3181

解题思路
两种思路：
①分辨不同直线，去重相同直线：利用一般式 ax+by+c=0 或 y=kx+b 来判断是否为一条直线
k的求法 n=gcd（x1-x2,y1-y2） k=((x1-x2)/n)/((y1-y2)/n) m=gcd((x1-x2)/n,(y1-y2)/n) bx=(x1-x2)/n/m
by=(y1-y2)/n/m b=bx/by
②求最短同直线距离，并以x或y坐标限制前后端点判断是否是最长直线：最短距离 x=(x1-x2)/n y=(y1-y2)/n
本代码中y为负数的情况:

#include 
#include 
#define X 20
#define Y 21

typedef struct
{
     
    int x;
    int y;
} Dian;

int gcd(int a,int b)
{
     
    if(a<0)
        a=-a;
    if(b<0)
        b=-b;
    int r;
    while(b!=0)
    {
     
        r=a%b;
        a=b;
        b=r;
    }
    return a;
}

int main()
{
     
    Dian d[X][Y];
    int i,j,x,y,k,l;

    for(i=0;i<X;i++)
        for(j=0;j<Y;j++)
    {
     
        d[i][j].x=i;
        d[i][j].y=j;
    }

    int ans=0;
    for(i=0;i<X;i++)
        for(j=0;j<Y;j++)
    {
     
        for(k=i;k<X;k++)    //以x限制点的前后
            for(l=0;l<Y;l++)   //注意y的上下并没有被限制所以最小距离比的y有负数
        {
     
            x=d[k][l].x-d[i][j].x;
            y=d[k][l].y-d[i][j].y;
            if(x==0 || y==0)    //斜率为0和斜率不存在的直线
                continue;
            int n=gcd(x,y);
            x=x/n;
            y=y/n;     //同直线最短距离

             //判断是否是最长的直线
            if(d[i][j].x-x>=0 && d[i][j].y-y>=0 && d[i][j].y-y<Y)  //对前端点的判断第三个条件是y为负数的情况
                continue;

            if(d[k][l].x+x<X && d[k][l].y+y<Y && d[k][l].y+y>=0)   //后端点的判断
                continue;
            ans++;
        }
    }
    printf("%d",ans+X+Y);
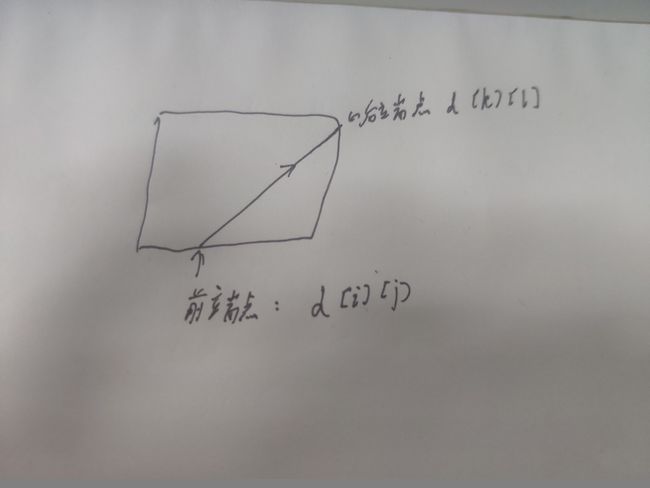
    return 0;
}

答案:40257

解题思路
16位数没有超过longlong
我们可以算出按小到大的顺序算出三个因数然后来组合排列

#include 
#include 
#include 

typedef long long ll;

int main()
{
     
    ll n=2021041820210418;
    int ans=0;

    for(ll a=1;a<sqrt(n);a++)
        if(n%a==0)
    {
     
        ll nn=n/a;
        for(ll b=1;b<sqrt(nn);b++)
        {
     
            if(nn%b==0)
            {
     
                ll c=nn/b;

                //三个相同加一 两个相同加三 没有相同加六
                if(a<=b && b<=c)
                {
     
                    if(a==b && b==c)
                        ans+=1;
                    if(a==b && b!=c)
                        ans+=3;
                    if(a!=b && b==c)
                        ans+=3;
                    if(a!=b && b!=c)
                        ans+=6;
                }
            }
        }
    }
    printf("%d",ans);

    return 0;
}

答案:2430

解题思路
简单的成无向图然后可以用Floyd和Djstra算法求最小权值(Floyd会比较慢)

Djstra:

#include 
#include 
#define INF 999999999

int arc[2022][2022];
int lcm(int a,int b)
{
     
    int r;
    int x=a,y=b;
    while(b!=0)
    {
     
        r=a%b;
        a=b;
        b=r;
    }

    return x*y/a;
}

void Djstra(int D[],int v)
{
     
    int i,w,min,k;
    int final[2022]={
     0};

    for(i=1;i<=2021;i++)
        D[i]=arc[v][i];
    D[v]=0;
    final[v]=1;  //自己到自己需要标记
    for(i=2;i<=2021;i++)
    {
     
        min=INF;
        for(w=1;w<=2021;w++)
        {
     
            if(!final[w] && D[w]<min)
            {
     
                min=D[w];
                k=w;
            }
        }
        final[k]=1;
        for(w=1;w<=2021;w++)
        {
     
            if(!final[w] && D[w]>min+arc[k][w])
            {
     
                D[w]=min+arc[k][w];      //将本不相连的点通过中介连接或算出新的距离
            }
        }
    }
}

int main()
{
     
    int i,j,D[2022];

    //初始化
    for(i=1;i<2022;i++)
        for(j=1;j<2022;j++)
         arc[i][j]=INF;

    for(i=1;i<2022;i++)
        for(j=i+1;j<2022;j++)
    {
     
        if(j-i<=21)
        {
     
            arc[i][j]=lcm(i,j);
            arc[j][i]=arc[i][j];
        }
    }

    Djstra(D,1);
    printf("%d",D[2021]);
    return 0;
}

Floyd:

#include 
#include 
#define INF 999999999
int arc[2022][2022];
int D[2022][2022];

int lcm(int a,int b)
{
     
    int x=a,y=b,r;
    while(b!=0)
    {
     
        r=a%b;
        a=b;
        b=r;
    }
    return x*y/a;
}

void Floyd()
{
     
   int i,j,k;

   for(i=1;i<=2021;i++)
    for(j=1;j<=2021;j++)
      D[i][j]=arc[i][j];

   for(i=1;i<=2021;i++)
    for(j=1;j<=2021;j++)
    for(k=1;k<=2021;k++)
   {
     
       if(D[i][k]>D[i][j]+D[j][k])
        D[i][k]=D[i][j]+D[j][k];
   }
}

int main()
{
     
    int i,j;

    for(i=1;i<=2021;i++)
        for(j=1;j<=2021;j++)
        arc[i][j]=INF;

    for(i=1;i<=2021;i++)
        for(j=i+1;j<=2021;j++)
    {
     
        if(j-i<=21)
        {
     
            arc[i][j]=lcm(i,j);
            arc[j][i]=arc[i][j];
        }
    }
    Floyd();
    printf("%d",D[1][2021]);
    return 0;
}

答案：10266837

解题思路
水题不说了

#include 
#include 
//99999999999999999
int main()
{
     
    long long int n;
    scanf("%lld",&n);

    n=n%(24*60*60*1000);
    int H,M,S;
    H=n/(60*60*1000);
    M=n%(60*60*1000)/(60*1000);
    S=n%(60*60*1000)%(60*1000)/1000;
    if(H<10)
        printf("0%d:",H);
    else
        printf("%d:",H);
    if(M<10)
        printf("0%d:",M);
    else
      printf("%d:",M);
    if(S<10)
     printf("0%d",S);
    else
        printf("%d",S);
    return 0;
}

解题思路
DFS暴力骗分，正解是dp也很简单
初始状态dp【sum】肯定是能够组成的，我们设定为1
利用自顶向下的思维动态转移方程：
dp【i】|=dp【i-w【j】】 这是只有左边放砝码的情况，我们可以自顶向下求出各种组合
dp【i】|=dp【i-2w【j】】 这是右边存在砝码的情况，相当于从左边抽出一个放到右边 重量为sum-2w【i】

注意哦：砝码不能重复使用不然写法会不同。

砝码重复
for(i=sum;i>0;i--)
for(j=0;j<n;j++)

DFS：

#include 
#include 
#define N 103

int flag[100000];
int vis[N];
int n,ans=0;
void dfs(int a[],int x)
{
     
    if(n<0)
    {
     
        n=0;
      return;
    }
    if(!flag[n])   //不能返回让他继续加
    {
     
        //printf("%d ",n);
        flag[n]=1;
        ans++;
    }
    for(int i=0;i<x;i++)
    {
     
        if(!vis[i])
        {
     
            int t=n;
            n=t-a[i];
            vis[i]=1;
            dfs(a,x);  //减的dfs
            n=t+a[i];
            dfs(a,x);  //加的dfs
            vis[i]=0;
            n=t;
        }
    }
}

int main()
{
     
    int a[N],n,i;
    scanf("%d",&n);
    for(i=0;i<n;i++)
        scanf("%d",&a[i]);
    dfs(a,n);
    printf("%d",ans-1);  //把0的情况减去
    return 0;
}

DP正解:

#include 
#include 
#define M 100003
#define N 103

int main()
{
     
    int w[N],n,i,j,sum=0;
    int dp[M]={
     0};
    scanf("%d",&n);

    for(i=0;i<n;i++)
    {
     
        scanf("%d",&w[i]);
        sum+=w[i];
    }

    dp[sum]=1;
    for(i=0;i<n;i++)   //砝码不重复的写法
     for(j=1;j<=sum;j++)
     {
     
         if(dp[j])
         {
     
             if(j>w[i])
                dp[j-w[i]]=1;   //砝码都在左边
             if(j>2*w[i])
                dp[j-2*w[i]]=1;  //有砝码放右边
         }
     }

    int ans=0;
    for(i=1;i<=sum;i++)
        if(dp[i])
        ans++;
    printf("%d",ans);

    return 0;
}

解题思路
用一个数组保存上一层的杨辉三角算出本层的杨辉三角，以此循坏直到寻到输入的数（骗分思路）

#include 
#include 

long long int a[10000]={
     1};
long long int last[10000]={
     1};
int main()
{
     
    int n;
    scanf("%d",&n);
    int i,j,count,flag=0;
    for(i=1;;i++)
    {
     
      for(j=0;j<i;j++)
      {
     
          if(j==0 || j==i-1)
          {
     
              count++;
              a[j]=1;
              last[j]=a[j];
              continue;
          }
          a[j]=last[j-1]+last[j];
          count++;
          if(a[j]==n)
          {
     
              flag=1;
              break;
          }
      }
      if(flag)
        break;
      for(j=0;j<i;j++)
        last[j]=a[j];
    }
    printf("%d",count);
    return 0;
}

解题思路
写了两个快排来骗分

#include 
#include 

//从小到大
void q_sort_mi(int a[],int start,int end)
{
     
    if(start>end) return;
    int i=start;
    int j=end;
    int temp=a[start];

    while(i<j)
    {
     
        while(i<j && a[j]>=temp)
            j--;
        if(i<j)
        {
     
            a[i]=a[j];
            i++;
        }
        while(i<j && a[i]<=temp)
            i++;
        if(i<j)
        {
     
            a[j]=a[i];
            j--;
        }
    }
    a[i]=temp;
    q_sort_mi(a,start,i-1);
    q_sort_mi(a,i+1,end);
}

//从大到小
void q_sort_ma(int a[],int start,int end)
{
     
    if(start>end)
        return;
    int i=start;
    int j=end;
    int temp=a[start];

    while(i<j)
    {
     
        while(i<j && a[j]<=temp)
            j--;
        if(i<j)
        {
     
            a[i]=a[j];
            i++;
        }
        while(i<j && a[i]>=temp)
            i++;
        if(i<j)
        {
     
            a[j]=a[i];
            j--;
        }
    }
    a[i]=temp;
    q_sort_ma(a,start,i-1);
    q_sort_ma(a,i+1,end);
}

int main()
{
     
    int a[6000],i;
    for(i=0;i<6000;i++)
        a[i]=i+1;
    int n,m,mode,end;
    scanf("%d%d",&n,&m);
    for(i=0;i<m;i++)
    {
     
        scanf("%d%d",&mode,&end);
        if(mode==0)
            q_sort_ma(a,0,end-1);
        else if(mode==1)
            q_sort_mi(a,end-1,n-1);
    }
    for(i=0;i<n;i++)
        printf("%d ",a[i]);
    return 0;
}

不会。。