力扣993 二叉树的堂兄弟节点——二叉树上的BFS

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：

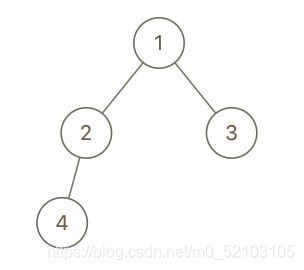
输入：root = [1,2,3,4], x = 4, y = 3
输出：false
示例 2：

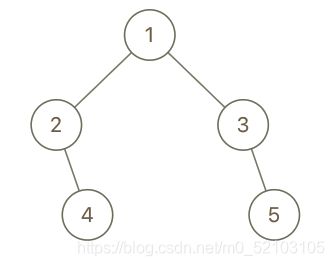
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true
示例 3：

输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

提示：

二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cousins-in-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

include <stdio.h>
#include 
#include 
struct TreeNode{
     
  int val;
  struct TreeNode *left;
  struct TreeNode *right;
};

typedef struct node{
     
    int parent;
    int step;
    struct TreeNode item;
    struct node *next;
}Node;

typedef struct{
     
    struct node *front;
    struct node *rear;
    int size;
}Queue;

void InitQueue(Queue *q)
{
     
    q->size=0;
    q->front=NULL;
    q->rear=NULL;
}

bool isEmpty(Queue *q){
     
    if(q->size==0)
        return true;
    return false;
}

void DeQueue(Queue *q,Node *t)
{
     
    Node *temp = q->front;
    if(isEmpty(q))
        return;
    q->front = q->front->next;
    q->size--;
    *t = *temp;
    free(temp);
    if(isEmpty(q))
        q->rear = NULL;
}

void EnQueue(Queue *q,struct TreeNode *t,int step,int parent)
{
     
    struct node *pnew = (struct node *)malloc(sizeof(struct node));
    pnew->next = NULL;
    pnew->step = step;
    pnew->item = *t;
    pnew->parent = parent;
    if(isEmpty(q))
    {
     
        q->front = q->rear = pnew;
        q->size++;
    }
    else
    {
     
        q->rear->next = pnew;
        q->rear = pnew;
        q->size++;
    }
}

bool isCousins(struct TreeNode* root, int x, int y){
     
    Queue q;
    Node t;
    int flx=0,fly=0;
    int place_x,place_y;
    int x_parent,y_parent;
    InitQueue(&q);
    EnQueue(&q,root,0,1);
    while(!isEmpty(&q))
    {
     
        DeQueue(&q,&t);
        if(flx==0 && t.item.val==x)
        {
     
            place_x=t.step;
            x_parent=t.parent;
            flx=1;
        }
        if(fly==0 && t.item.val==y)
        {
     
            place_y=t.step;
            y_parent=t.parent;
            fly=1;
        }
        if(fly && flx)
        {
     
            if(place_x==place_y && x_parent != y_parent)
                return true;
            else
                return false;
        }
     if(t.item.left!=NULL)
        EnQueue(&q,t.item.left,t.step+1,t.item.val);
      if(t.item.right!=NULL)
        EnQueue(&q,t.item.right,t.step+1,t.item.val);
    }
}

void CreatTree(struct TreeNode **root)
{
     
    int val;
    scanf("%d",&val);
    if(val==1234)
    {
     
        *root = NULL;
    }
    else
    {
     
        struct TreeNode *pnew = (struct TreeNode *)malloc(sizeof(struct TreeNode));
        pnew->val = val;
        pnew->left = NULL;
        pnew->right = NULL;
        *root = pnew;
        CreatTree(&(pnew->left));
        CreatTree(&(pnew->right));
    }
}

void PrintTree(struct TreeNode *root)
{
     
    if(root)
    {
     
        PrintTree(root->left);
        printf("%d ",root->val);
        PrintTree(root->right);
    }
}

int main()
{
     
    struct TreeNode *root;
    CreatTree(&root);
    PrintTree(root);
    putchar('\n');
    int x,y;
    scanf("%d%d",&x,&y);
    bool flag=isCousins(root,x,y);
    if(flag)
        puts("Yes");
    else
        puts("No");
    return 0;
}