超分辨论文阅读笔记:SAN
SAN;Second-order Attention Network for Single Image Super-Resolution阅读笔记
SAN
- SAN;Second-order Attention Network for Single Image Super-Resolution阅读笔记
-
- 1.Introduction
- 2.Related Work
- 3.Second-order Attention Network
-
- 3.1Network Framework
- 3.2Non-locally Enhanced Residual Group(NLRG)
- 3.3.Second-order Channel Attention(SOCA)
- 3.4协方差标准化
文章链接:2019CVPR,图像超分辨SAN
SAN摘要:基于CNN的超分辨方法虽然取得了最好的结果,但此类方法关注更宽或更深的结构设计,忽略了中间层特征之间的关系,本文提出二阶注意力网络,以达到更强的特征表达和特征关系学习。具体来说:本文开发了一种新的二阶通道注意力模块,能够自适应的调整通道特征来获得更有区别性的表示,另外,本文提出了一种非局部残差加强结构,不仅包含了非局部操作而且有多个局部信息注意力块,用于学习日益抽象的特征表示。
1.Introduction
单幅图像超分辨引起了广泛关注,通俗的说,超分辨的目标是输入低分辩得到一个视觉上的高分辨图像,由于多个不同的HR版图像可以映射到同一个LR图像,因此作为一个逆问题超分辨是不适定的。
基于模型的方法虽然能灵活的生成高质量的HR图像,但优化困难时间复杂度高,当图像信息分布与获得的先验差距较大时,其效果会迅速下降。
深度卷积神经网络最近在各种问题上取得了空前的成就,CNN因为其强大的特征表示和端到端的训练参数使其成为解决超分辨问题的一种有效方案,最近几年,提出了大量的基于CNN的方法来学习LR与HR之间的映射关系,通过充分的探索训练数据中图像的先验信息,CNN在超分辨领域取得了目前最优的结果,但基于CNN的方法仍然存在一些局限性:1.不能充分利用LR图像的信息,导致性能较差,2.大多数CNN方法主要关注设计更深或更宽的网络学习更具有区分性的特征,很少有模型去探索特征之间的固有联系,因此阻碍了CNN的表达能力。
本文提出了二阶注意力机制(SOCA)更好的学习特征之间的联系,此模块通过利用二阶特征的分布自适应的学习特征的内部依赖关系,SOCA的机制是网络能够专注于更有益的信息且能够提高判别学习的能力,此外,本文提出了一种非局部加强残差组结构能进一步结合非局部操作来提取长程的空间上下文信息。通过堆叠非局部残差组,本文的方法能够利用LR图像的信息且能够忽略低频信息,
本文贡献主要有以下三点:
1.提出了用于图像超分辨的深度二阶注意力网络,
2.提出了二阶注意力机制通过利用高阶的特征自适应的调整特征,另外利用了协方差归一化的方法来加速网络的训练。
3.提出了非局部加强残差组NLRG结构构建网络,进一步结合非局部操作来提取空间上的上下文信息,并共享残差结构来学习深度特征,另外通过跳跃链接来过滤低频信息且简化了深层网络的训练。
2.Related Work
基于CNN的超分辨方法:基于CNN的方法由于其强大的非线性表达能力在超分辨领域被广泛的研究,一般情况下,超分辨问题被视为一个图像到图像的回归问题,大多数方法致力于设计更宽或更深的网络结构,SRCNN首次将CNN引入超分辨领域,KIM等设计了更深的VDSR和DRCN,其层数超过了16层,Lim等人提出了堆叠残差块的EDSR,显著的性能表明,表示网络深度在图像超分辨中的重要性,MemNet和RDN都是基于dense的方法,致力于使用所有卷积层的高频信息,另外NLRN和RCAN通过考虑空间和通道维度之间的关系来提高性能。
Attention mechanism
SENet虽然被引入超分辨领域,但其只探索只探索了一阶的图像特征,而忽略了更高阶的图像特征,因此阻碍了网络的判别性能力,在图像超分辨领域高频信息的特征对于HR重建非常重要,因此本文提出了二阶注意力机制,
3.Second-order Attention Network
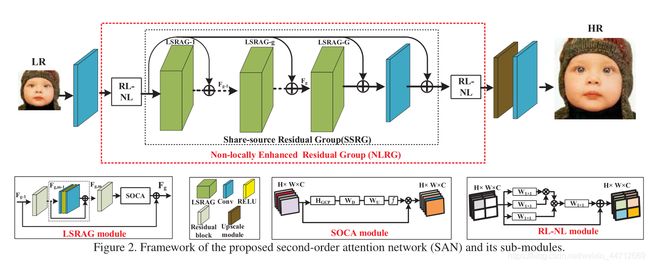
3.1Network Framework
SAN由4个部分组成:浅层的特征提取,基于特征提取的非局部加强残差组(NLRG),上采样模块,重建部分,本文只用了一个卷积层来提取浅层特征 F 0 F_{0} F0:
F 0 = H S F ( I L R ) F_{0}=H_{SF}(I_{LR}) F0=HSF(ILR), H S F ( . ) H_{SF}(.) HSF(.)表示卷积操作,然后将 F 0 F_{0} F0被用于NLRG,公示表示如下:
F D F = H N L R G ( F 0 ) F_{DF}=H_{NLRG}(F_{0}) FDF=HNLRG(F0)此处的 H N L R G H_{NLRG} HNLRG表示基于深度特征提取NLRG模块,包含了几个扩大感受野的非局部模块以及G个局部残差注意力组(LSRAG)模块,因此本文的NLRG能够达到非常深的深度,从而获得了非常大的感受野。
最终通过上采用模块进行上采样:
F ↑ = H ↑ ( F D F ) F_{\uparrow}=H_{\uparrow}(F_{DF}) F↑=H↑(FDF),这里的 H ↑ ( . ) H_{\uparrow}(.) H↑(.)和 F ↑ F_{\uparrow} F↑分别代表上采用模块和上采样特征,
I S R = H R ( F ↑ ) = H S A N ( I L R ) I_{SR}=H_{R}(F_{\uparrow})=H_{SAN}(I_{LR}) ISR=HR(F↑)=HSAN(ILR) 这里的 H R ( . ) , H S A N H_{R}(.),H_{SAN} HR(.),HSAN分别代表重建层和SAN.
SAN可以通过损失函数进行优化,本文使用了 L 1 L_{1} L1作为损失函数,最终的LOSS表示如下:
L ( Θ ) = 1 N ∑ i = 1 N ∣ ∣ H S A N ( I L R i ) − I H R i ∣ ∣ 1 L(\Theta)=\frac{1}{N}\sum_{i=1}^{N}||H_{SAN}(I^{i}_{LR})-I^{i}_{HR}||_{1} L(Θ)=N1∑i=1N∣∣HSAN(ILRi)−IHRi∣∣1
3.2Non-locally Enhanced Residual Group(NLRG)
NLRG如图所示,其包含了数个局部的非局部(RL-NL)模块和一个共同的残差组结构(SSRG),RL-NL提取了LR特征丰富的结构信息和HR场景中自相似性。SSRG模块有G个局部残差注意力组LSRAG和共享跳跃链接组成。每个LSRAG进一步包含了M个简单的残差块和局部跳跃链接,之后时SOCA进一步利用特征的相互依赖性。
堆叠残差块有助于形成深度CNN,但以此构建的非常深的网络会由于梯度消失和梯度爆炸而训练困难且性能难以提升,受到深度laplacian金字塔网络的启发,本文提出局部残差注意力机制(LSRAG)作为基础单元,但简单的堆叠块很难获得更好的结果,为了解决这个问题,在NLRG引入了共享跳跃链接,不止便于网络的训练,而且能够过滤低频信息,LSRAG的第G个组表示为: F G = W S S C F 0 + H g ( F g − 1 ) F_{G}=W_{SSC}F_{0}+H_{g}(F_{g-1}) FG=WSSCF0+Hg(Fg−1),
这里的 W S S C W_{SSC} WSSC表示卷积层的权重,省略了偏置项, H g ( . ) H_{g}(.) Hg(.)表示第g个LSRAG, F g F_{g} Fg表示第g个LSRAG的输出,得到的深度特征可以表示为:
F D F = W S S C F 0 + F G F_{DF}=W_{SSC}F_{0}+F_{G} FDF=WSSCF0+FG
SSRG结构布置有利于跨层信息的交流,能够训练出非常深的网络进一步提高模型性能
RL-NL:Region-level non-local module
传统的全局等级的非局部操作有以下几点限制:1.计算量大,尤其特征尺寸较大时,2.经验表明,对于低级图像任务,合适的邻域大小的局部操作效果更好。因此对于分辨率更高的图像特征或退化的特征,执行局部的非局部操作是更好的选择,由于这些原因,本文将特征分成了几个区域,如上图所示,输入特征被分为尺寸相同的 k 2 k^{2} k2大小的块,然后将其输入到后续的层,,
Local-source residual attention group:
通过共享跳跃链接,可以过滤低频信息,为了进一步进行残差学习,本文堆叠了M个简单的残差块来构建LSRAG,第g个LSRAG中的第m个残差块表示为:
F g , m = H g , m ( F g , m − 1 ) F_{g,m}=H_{g,m}(F_{g,m-1}) Fg,m=Hg,m(Fg,m−1)
这里的 H g , m ( . ) H_{g,m}(.) Hg,m(.)表示其操作,两个F分别表示其输入和输出,为了让网络能够拥有更多的信息性的特征,添加了局部跳跃链接:
F g = W g F g − 1 + F g , M F_{g}=W_{g}F_{g-1}+F_{g,M} Fg=WgFg−1+Fg,M
这里的 W g W_{g} Wg指的是相应的权重,为了更获得判别性更强的信息,本文提出了SOCA机制,嵌入在LSRAG的末端,此机制通过二阶特征信息学习自适应的通道放缩。
3.3.Second-order Channel Attention(SOCA)
Covariance normalization: 协方差标准化,将一个HWC的特征F=[f1,…fc],将其形状转化为一个特征矩阵,样本协方差矩阵的计算表示为:
∑ = X I ‾ X T \sum=X\overline{I}X^{T} ∑=XIXT, I ‾ = 1 s ( I − 1 s 1 ) \overline{I}=\frac{1}{s}(I-\frac{1}{s}1) I=s1(I−s11),
I和1是s*s的协方差矩阵和单位矩阵。文献[19][20]中表明协方差标准化对获得更有判别性的信息有关键作用,,因此本文首先用获得的协方差矩阵 ∑ \sum ∑做协方差归一化,此矩阵是对称正定的,其特征值分解为:
∑ = U Λ U T \sum=U\Lambda U^{T} ∑=UΛUT,
U是正交矩阵, Λ \Lambda Λ指的是特征值在不递增时的对角矩阵,
协方差归一化转换成特征值的幂:
Y ^ = ∑ α = U Λ α U T \hat{Y}=\sum^{\alpha}=U\Lambda^{\alpha }U^{T} Y^=∑α=UΛαUT,
α \alpha α表示一个正实数, Λ α \Lambda^{\alpha } Λα表示对角矩阵,当 α = 1 \alpha=1 α=1时,不需要标准化,当其<1时,会非线性的收缩大于1.0的特征值,在[19]中表明了, α = 0.5 \alpha=0.5 α=0.5能够获得更有判别性的特征。因此本文设置 α \alpha α,
Channel attention: 标准化协方差矩阵表征了通道特征之间的相关性,本文通过全局协方差池化将标准化矩阵作为通道描述符, Y ^ = [ y 1 . . . . . . y C ] \hat{Y}=[y_{1}......y_{C}] Y^=[y1......yC],
通过收缩 Y ^ \hat{Y} Y^可以获得通道信息表征 Z ∈ R C × 1 Z\in R^{C\times1} Z∈RC×1,第c个维度的z的计算表示为:
z c = H G C P ( y c ) = 1 C ∑ i c y c ( i ) z_{c}=H_{GCP}(y_{c})=\frac{1}{C} \sum^{c}_{i}y_{c}(i) zc=HGCP(yc)=C1∑icyc(i),
H G C P ( . ) H_{GCP}(.) HGCP(.)表示全局协方差池化函数,与一阶池化相比, 全局协方差池化能够获得更高阶的特征信息和更具有判别性的特征信息,为充分利用聚合信息中的特征依赖关系,本文采用了一种门控机制,利用sigmoid函数作为一种简单的门控函数:
w = f ( W U δ ( W D Z ) ) w=f(W_{U}\delta(W_{D^{Z}})) w=f(WUδ(WDZ)),
此处的 W D W_{D} WD和 W U W_{U} WU是卷积层的权重,特征通道为C/r和C,f(.)表示sigmoid函数, δ \delta δ表示RELU函数,最后通过 w c w_{c} wc来对注意力权重进行缩放:
f c ^ = w c ⋅ f c \hat{f_{c}}=w_{c}\cdot f_{c} fc^=wc⋅fc
w c w_{c} wc和 f c f_{c} fc表示尺度因子和特征映射,通过通道注意力,LSRAG的残差分量可以被自适应的调整。
综上所述,协方差归一化在SOCA中起着重要的作用,但其严重依赖特征值分解,不能在GPU平台得到很好的支持,从而导致训练困难,因此本文采用了基于牛顿-舒尔兹迭代的快速矩阵归一化方法
3.4协方差标准化
在GPU平台快速实现特征值分解仍然是一个困难的问题,本文通过牛顿-舒尔兹迭代快速实现协方差归一化的计算, ∑ \sum ∑的平方根为 ∑ 1 / 2 = Y = U d i a g ( λ i 1 / 2 U T ) \sum^{1/2}=Y=Udiag(\lambda_{i}^{1/2}U^{T}) ∑1/2=Y=Udiag(λi1/2UT),给初值 Y 0 = ∑ , Z 0 = I Y_{0}=\sum,Z_{0}=I Y0=∑,Z0=I,更新公式如下:
Y n = 1 2 Y n − 1 ( 3 I − Z n − 1 Y n − 1 ) Y_{n}=\frac{1}{2}Y_{n-1}(3I-Z_{n-1}Y_{n-1}) Yn=21Yn−1(3I−Zn−1Yn−1)
Z n = 1 2 ( 3 I − Z n − 1 Y n − 1 ) Z n − 1 Z_{n}=\frac{1}{2}(3I-Z_{n-1}Y_{n-1})Z_{n-1} Zn=21(3I−Zn−1Yn−1)Zn−1
经过重复迭代之后, Y n 和 Z n Y_{n}和Z_{n} Yn和Zn将二次收敛到Y和 Y − 1 Y_{-1} Y−1,此方法能够经过很少的迭代就得到近似解,
由于此迭代方法旨在局部收敛,为保证收敛,首先对 ∑ \sum ∑进行预标准化:
∑ ^ = 1 t r ( ∑ ) ∑ \hat{\sum}=\frac{1}{tr(\sum)}\sum ∑^=tr(∑)1∑,此处 t r ( ∑ ) = ∑ C i λ i tr(\sum)=\sum_{C}^{i}\lambda_{i} tr(∑)=∑Ciλi表示 ∑ \sum ∑的轨迹,可以推断出 ∣ ∣ ∑ − I ∣ ∣ 2 ||\sum-I||_{2} ∣∣∑−I∣∣2,等于 ( ∑ − I ) (\sum-I) (∑−I)的最大奇异值,因此保证了收敛的条件。
经过此迭代之后,本文通过后补偿对预归一化的数据量进行补偿,最终的标准化协方差矩阵为:
Y ^ = t r ( ∑ ) Y N \hat{Y}=\sqrt{tr(\sum)}Y_{N} Y^=tr(∑)YN