第一行两个正整数n和m,代表花海的大小
接下来n行每行一个长度为m的01串,描述花海中的每一个点
其中0代表可以走,1代表这个点被小妖精封住辣~
数据保证花海的左上角和右下角没有小妖精
【弱省胡策】Round #0 Flower Dance DP
Flower Dance
Time Limit: 20 Sec Memory Limit: 256 MB
题目连接
http://162.105.80.126/contest/%E3%80%90%E5%BC%B1%E7%9C%81%E8%83%A1%E7%AD%96%E3%80%91Round%20%230/Flower%20Dance
Description
萌萌哒的TKD正在打代码,耳边放着Flower Dance,手指轻快地在键盘上舞动。
听着这美妙的旋律,TKD不禁想起了什么。
第一次遇到Po姐姐的时候,就一起欣赏了美丽的花舞吧。
两个人自由地在花海中徜徉...徜徉......
那真的是段美妙的回忆呢~
欣赏花舞之后,腹黑的Po姐姐和TKD聊了起来。
‘TKD啊,你还记得我们是怎么走过花海的吗?’
‘唔...貌似记得不是太清楚了>v<’
‘我刚才观察了一下,其实花海中能走的路,就是一个n*m的网格图’
‘哦?是吗OwO’
‘然后呢,有一些节点被调皮的小妖精堵住了,是不能走的’
‘嗯是的,好可爱的妖精呢>_<’
‘即便如此我们还是都走了最短的路径呢~’
‘嗯嗯!~’
‘而且我还刻意走了一条和你走的路不相交的路哦~’
‘姐姐真是厉害呀,连我走的路是什么都知道~~~’
‘当然啊,姐姐可比你厉害多了。现在我考考你,我们从左上角走到右下角,只能向右或者向下走,有多少总走法呢?’
‘啊——?’
萌萌哒的TKD完全没有想到Po姐姐会如此腹黑。
你能帮TKD解答腹黑姐姐的问题吗~
Input
Output
一行一个整数,代表Po姐姐和TKD从左上角走到右下角的方案数
答案对1000000007(109+7)取模
注意:对于两条不相交的路径A和B,如果Po姐姐走了A,TKD走了B,和Po姐姐走了B,TKD走了A我们视为同一种方案。
Sample Input
4 4 0001 0100 0000 0000
Sample Output
HINT
- 对于20%的数据,
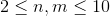
- 对于40%的数据,
- 对于另外10%的数据,花海中不存在小妖精
- 对于100%的数据,
五种方案如下图所示:
题意
题解:
DP,我们可以分析一下,从上面走的,必然是从(1,2)走到(n-1,m),下面走的,必然是从(2,1)走到(n,m-1)位置
我们可以跑一法dp,从(1,2)走到(n-1,m)的总类数,从(2,1)走到(n,m-1)的种类数
但是很显然,我们把相交的情况也考虑进去了,相交的情况,其实可以转化一下,就变成从(1,2)走到(n,m-1),从(2,1)走到(n-1,m)的种类数相乘法
因为不管怎么走,这样子必然会有一个交点,就把所有相交的情况都囊括进去了,然后乱搞就好了
代码:
//qscqesze #include <cstdio> #include <cmath> #include <cstring> #include <ctime> #include <iostream> #include <algorithm> #include <set> #include <vector> #include <sstream> #include <queue> #include <typeinfo> #include <fstream> #include <map> #include <stack> typedef long long ll; using namespace std; //freopen("D.in","r",stdin); //freopen("D.out","w",stdout); #define sspeed ios_base::sync_with_stdio(0);cin.tie(0) #define test freopen("test.txt","r",stdin) #define maxn 200001 #define mod 1000000007 #define eps 1e-9 int Num; char CH[20]; //const int inf=0x7fffffff; //нчоч╢С const int inf=0x3f3f3f3f; inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } inline void P(int x) { Num=0;if(!x){putchar('0');puts("");return;} while(x>0)CH[++Num]=x%10,x/=10; while(Num)putchar(CH[Num--]+48); puts(""); } //************************************************************************************** int n,m; char s[3005][3005]; ll dp[3005][3005]; ll solve(int x,int y,int xx,int yy) { if(s[x][y]==1) return 0; memset(dp,0,sizeof(dp)); dp[x][y]=1; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(s[i][j]=='1') continue; dp[i][j]+=dp[i-1][j]+dp[i][j-1]; dp[i][j]%=mod; } } return dp[xx][yy]; } int main() { //test; n=read(),m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); ll tmp=solve(1,2,n-1,m)*solve(2,1,n,m-1)-solve(1,2,n,m-1)*solve(2,1,n-1,m); printf("%d\n",(tmp%mod+mod)%mod); }