面试题打卡——C++版

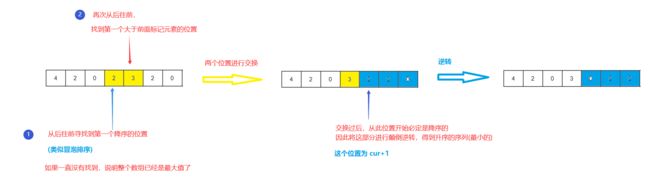
下一个排列

实现获取 下一个排列 的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

class Solution {
public:
    void nextPermutation(vector& nums) {
        int cur=nums.size()-2;

        while(cur>=0&&nums[cur]>=nums[cur+1])//前面大于后面的
        {
            cur--;
        }

        if(cur<0)//已经是最大数组了
            sort(nums.begin(),nums.end());
        else//表示找到了降序的一个位置
        {
            int pos=nums.size()-1;
            while(nums[pos]<=nums[cur])
            {
                pos--;
            }

            swap(nums[cur],nums[pos]);
            reverse(nums.begin()+cur+1,nums.end());
        }
        
    }
};

合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

class Solution {
public:

    struct Less
    {
        bool operator ()(vector&arr1,vector&arr2)
        {
            return arr1[0]> merge(vector>& intervals) {
        if(intervals.size()<2)//只有一个区间
            return intervals;

        sort(intervals.begin(),intervals.end(),Less());//按左端点进行排序

        vector> ret;
        ret.push_back(intervals[0]);
        int cur=1;
        while(cur

最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。

解题思路：

1.取出strs之中的一个字符串
2.用这个字符串一次依次与strs之中，后面的字符串进行比较，并且统计相出现相同的字符
3.如果第一个单词就不相等，直接返回空

class Solution {
public:
    string longestCommonPrefix(vector& strs) {
        if(strs.size()==0)
            return "";

        string str(strs[0]);
        int len=0;//标记匹配的长度

        for(auto&e:strs)
        {
            if(e[0]!=str[0])//第一个字符就不匹配
                return "";
            else//匹配了
            {
                int count=0;//记录匹配的单词个数
                for(int i=0;i

最接近的三数之和

给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

解题思路：

本题是要我们求从数组中取出三个数，组成的和最接近target，如果用最直观的方法即是三个for循环进行嵌套，此时的时间复杂度高达O(N^3)。

我们可以进行如下图所示的优化：

1.给定一个count先记录前面的三个数的和

2.先对数组进行排序

3.每次先确定一个中心点，然后给定左右两个指针，即可以得到三个数字的和num，此时有三种情况：
a.num==target直接进行返回；
b.num c.num>target,与上面相反，left–；

第二种情况，和第三种情况，我们要用得到的num和target进行比较，如果num更加的接近target，则更新count

class Solution {
public:
    int threeSumClosest(vector& nums, int target) {
        sort(nums.begin(),nums.end());//排序
        int ret=nums[0]+nums[1]+nums[2];

        int mid=1;
        while(mid=0&&right

螺旋矩阵II

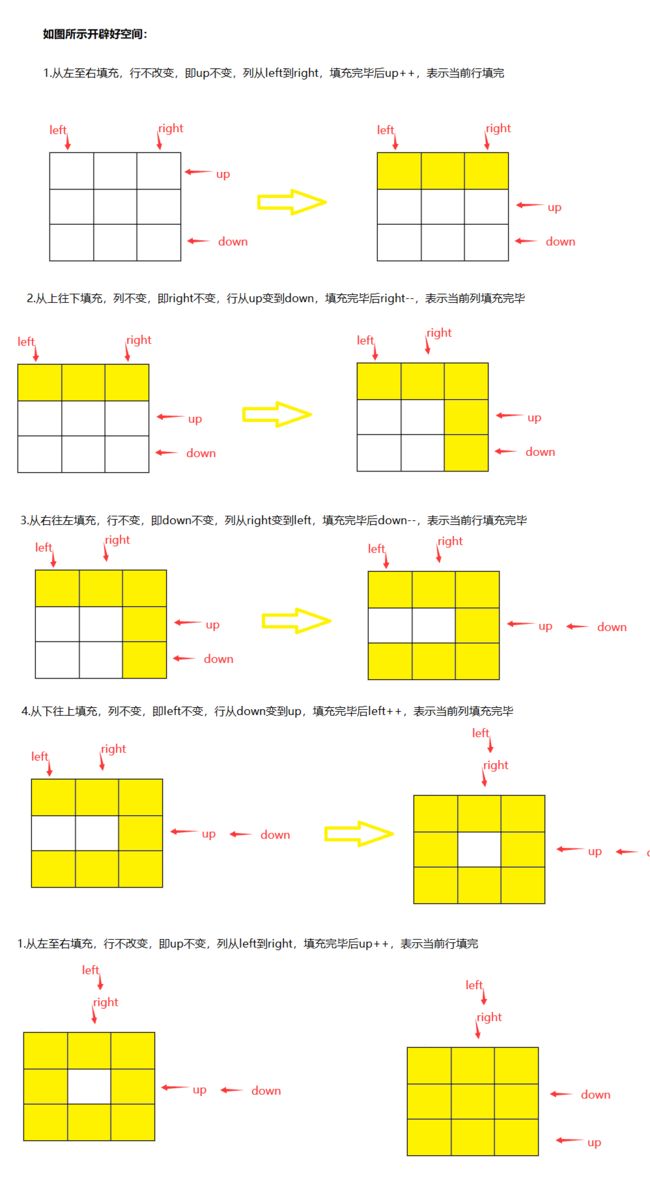
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

class Solution {
public:
    vector> generateMatrix(int n) {
        vector> ret(n,vector(n,0));

        int left=0;
        int right=n-1;
        int up=0;
        int down=n-1;
        int num=1;

        while(left<=right&&up<=down)
        {
            //if(up<=down)//从左至右，行不变->up不变
                for(int i=left;i<=right;i++)
                {
                    ret[up][i]=num++;
                }
                up++;//当前行已经补充完毕

          // 从上至下，列不变 ->right不变
                for(int i=up;i<=down;i++)
                {
                    ret[i][right]=num++;
                }
                right--;//当前列补充完毕

          // 从右至左，行不变 ->down不变
                for(int i=right;i>=left;i--)
                {
                    ret[down][i]=num++;
                }
                down--;//当前行补充完毕

           //从下至上，列不变 ->left不变
                for(int i=down;i>=up;i--)
                {
                    ret[i][left]=num++;
                }
                left++;//当前列补充完毕
        }
        return ret;
    }
};