Wu deeplearning.ai C2W1 assignment_Gradient+Checking

Gradient Checking

Welcome to the final assignment for this week! In this assignment you will learn to implement and use gradient checking. 

You are part of a team working to make mobile payments available globally, and are asked to build a deep learning model to detect fraud--whenever someone makes a payment, you want to see if the payment might be fraudulent, such as if the user's account has been taken over by a hacker. 

But backpropagation is quite challenging to implement, and sometimes has bugs. Because this is a mission-critical application, your company's CEO wants to be really certain that your implementation of backpropagation is correct. Your CEO says, "Give me a proof that your backpropagation is actually working!" To give this reassurance, you are going to use "gradient checking".

Let's do it!

这一章节主要介绍了一种检查反向传播是否发生错误的方法，数值逼近。在反向传播的过程中，我们可能在求导的过程中极可能出错，采用这种方法就可以确定我们推导的公式是正确的。

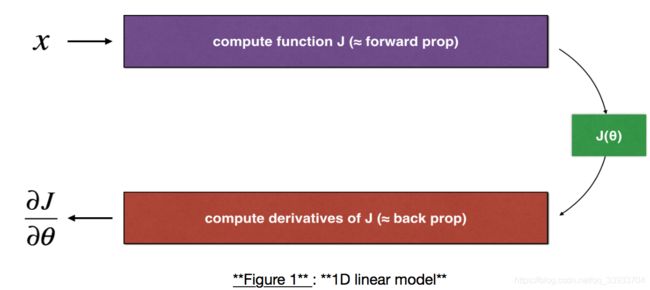
1、1-dimensional gradient checking

一层的梯度检查，简单来说，我们先正常的利用方向传播函数计算出，然后利用在领域极限的定义计算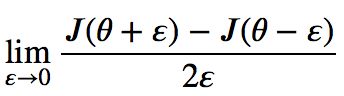然后在根据误差公示来判断是否出现了错误，如果difference的值小于10的-7次方，那么就是没有错误，反之就是有错误。

# Packages
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector

# GRADED FUNCTION: forward_propagation

def forward_propagation(x, theta):
    J = theta*x
    return J

# GRADED FUNCTION: backward_propagation

def backward_propagation(x, theta):
    dtheta = x
    return dtheta

# GRADED FUNCTION: gradient_check

def gradient_check(x, theta, epsilon = 1e-7):
    thetaplus = theta + epsilon                             # Step 1
    thetaminus = theta - epsilon                            # Step 2
    J_plus = forward_propagation(x, thetaplus)              # Step 3
    J_minus = forward_propagation(x, thetaminus)            # Step 4
    gradapprox = (J_plus - J_minus)/(2*epsilon)             # Step 5
    grad = backward_propagation(x, theta)
    numerator = np.linalg.norm(grad - gradapprox)           # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)   # Step 2'
    difference = numerator / denominator                    # Step 3'
    
    if difference < 1e-7:
        print ("The gradient is correct!")
    else:
        print ("The gradient is wrong!")
    
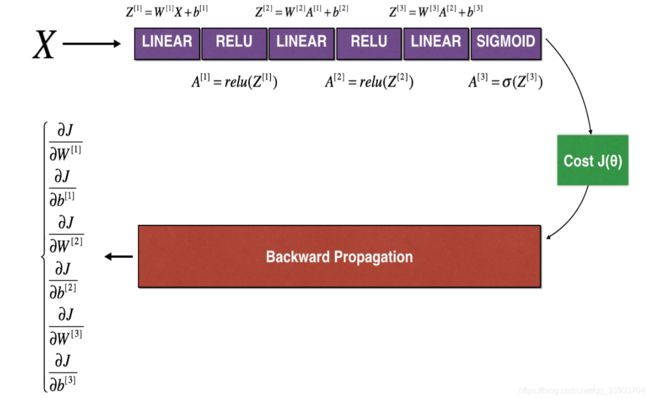
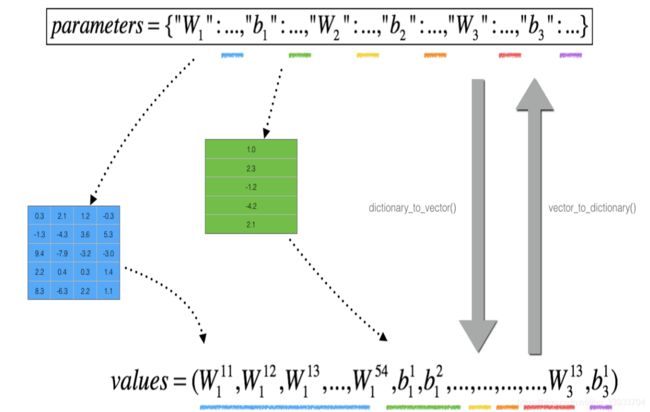
    return difference

2、N-dimensional gradient checking 

到了多层之后，总体的方法没有改变，就是多了一个向量化的步骤。

 

def forward_propagation_n(X, Y, parameters):
    # retrieve parameters
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)
    # Cost
    logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = 1./m * np.sum(logprobs)

    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
    
    return cost, cache

def backward_propagation_n(X, Y, cache):    
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache 
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T) * 2
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T)
    db1 = 4./m * np.sum(dZ1, axis=1, keepdims = True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

# GRADED FUNCTION: gradient_check_n

def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    # Compute gradapprox
    for i in range(num_parameters):
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        # "_" is used because the function you have to outputs two parameters but we only care about the first one
        thetaplus = np.copy(parameters_values)                   # Step 1
        thetaplus[i][0] = thetaplus[i][0] + epsilon              # Step 2
        J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))      # Step 3
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        thetaminus = np.copy(parameters_values)                  # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon            # Step 2        
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus))                                # Step 3
        
        # Compute gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i])/(2*epsilon)
    
    # Compare gradapprox to backward propagation gradients by computing difference.
    numerator = np.linalg.norm(grad - gradapprox)                                           # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)                                         # Step 2'
    difference = numerator / denominator                         # Step 3'

    if difference > 1e-7:
        print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
    else:
        print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference