容量耦合系数模型_期刊在线 | 基于ALE流固耦合方法的刷式密封泄漏特性理论与实验研究...
01
引言
刷式密封是一种广泛应用于航空发动机等透平机械的优良接触式动密封[]。近年来,随着透平机械逐渐向高参数方向发展,由刷式密封引起的泄漏损失越来越大,直接影响透平机械的工作效率。因此开展刷式密封的泄漏流动特性研究具有重要理论和实际意义。
国内外学者主要从理论分析与实验研究两方面对刷式密封的泄漏流动特性进行研究。在理论研究方面,国外Bayley和Long[4]首次采用多孔介质模型,在仅考虑粘性阻力的条件下数值计算了刷式密封的泄漏量;Chew等[]同时考虑了粘性阻力系数和惯性阻力系数的non-Darcian多孔介质模型,理论研究了刷式密封泄漏流动特性并与实验结果相对比。国内王之栎、丁水汀、黄学民等[]建立了多孔介质模型,理论分析了刷式密封泄漏流动特性的影响因素;邱波等[10]采用Ergun方程推导得出了刷丝束区域的粘性阻力系数表达式,并数值验证了刷式密封的泄漏量;张元桥等[]建立多孔介质传热模型,在考虑摩擦热效应的条件下,数值分析了不同工况参数对刷式密封泄漏量的影响;孙丹等[]建立了三维瞬态的流固耦合刷式密封求解模型,在考虑刷丝弯曲变形的条件下,分析了小压比条件下刷式密封泄漏特性的影响规律。
研究结果表明,考虑刷丝变形的瞬态流固耦合求解模型计算得出的泄漏量比多孔介质模型更精确。刷式密封刷丝在流体的作用下会产生变形,刷丝变形进一步影响流体分布,刷丝与流体之间的相互作用是典型的瞬态双向流固耦合问题[]。而传统的刷式密封流固耦合方法在计算时由于网格畸变,导致负体积问题,因此难以计算大压比条件下刷丝接触变形对刷式密封泄漏特性的影响。
在泄漏特性实验研究方面。国外学者Ferguson[18]首先建立了密封实验台,通过实验验证了刷式密封的密封性能远优于传统迷宫密封;Bayley等[19]通过建立静态刷式密封实验台,实验结果表明,随着压比的增大刷式密封泄漏量不断增大,同时测出了刷丝束区域的压力分布;Turner等[20]对Bayley和Long的刷式密封实验台进行改进,实验测量了两种间隙条件下的刷式密封的泄漏量和压力分布;Chupp等[21]进行刷式密封泄漏特性实验,验证了刷式密封泄漏量远低于迷宫密封,进出口压比的加载过程也会影响刷式密封的泄漏量。国内孙晓萍[22]进行刷式密封磨损与泄漏特性实验,发现随着磨损的增大,刷丝与转子之间的泄漏量会增大;曹广州等[23]实验研究了低转速条件下,刷式密封的泄漏量不断减少,后趋于稳定;胡广阳等[24]进行刷式密封磨损特性与泄漏特性实验。
结果表明,转速对泄漏量影响较少,刷式密封的密封性能远优于迷宫密封;杜春华等[25]研究了刷式密封在间隙、过渡和过盈三种条件下磨损特性对泄漏量的影响,在实验的初始阶段,过盈配合时磨损对泄漏影响最大,过盈配合时次之,间隙配合时最小。综上,现有文献对刷式密封泄漏特性实验研究方法比较单一,鲜有文献考虑刷丝接触变形对泄漏特性影响的论文公开发表。
本文提出基于ALE流固耦合方法的刷式密封三维瞬态双向流固耦合求解模型。考虑了刷丝接触变形对刷式密封泄漏特性的影响,在验证数值模型准确性的基础上,分析了刷式密封的流场分布特性,研究了压比、刷丝间隙、刷丝直径、刷丝排数等参数对刷式密封泄漏的影响规律,在验证ALE流固耦合方法准确性基础上,研究了不同结构参数对刷式密封泄漏特性的影响规律。
02
基于ALE流固耦合的刷式密封理论研究
2.1 刷式密封流固耦合特性分析
刷式密封三维模型如图1所示,刷丝束由柔软纤细的刷丝交错层叠构成,并沿着转子旋转方向呈一定角度排列,使刷丝对转子的瞬间径向变形或偏心运动具有更好的自适应性,保持良好的密封性能。研究表明,刷丝在气流力的作用下产生变形,刷丝变形进一步影响流场分布,刷丝与流体之间的相互作用是典型的流固耦合问题。当气流力较大时,刷丝的弯曲变形量也随之增大,且刷丝与刷丝之间产生接触碰撞,此时刷丝的运动状态对刷式密封的泄漏量将产生较大的影响。
Fig. 1 Schematic diagram of brush seal structure
2.2 基于ALE方法的刷式密封流体动力学模型
刷式密封流体采用ALE算法,ALE算法与Euler算法、Lagrange算法相比的优点在于其坐标系不固定,在空间也不依附于物体节点,网格可以做任意的运动,该方法可以克服大变形问题难题,主要用于求解流固耦合问题[26]。ALE算法可以计算刷丝接触和大变形,物质质点A在t时刻的空间坐标可表示为
| (1) |
式中A表示物质坐标,也称为拉格朗日坐标,t表示时刻。
网格运动可描述为
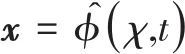 |
(2) |
式中![]() 为参考坐标系,也称为ALE坐标,它是指网格点的标记。
为参考坐标系,也称为ALE坐标,它是指网格点的标记。
由式(1)和(2)可知,质点A在t时刻所对应ALE坐标![]() 为
为
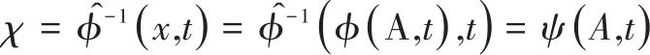 |
(3) |
质点A在参考坐标系中的运动速度(即质点参考速度)为
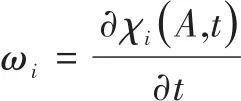 |
(4) |
网格点![]() 的位移、速度和加速度分别为
的位移、速度和加速度分别为
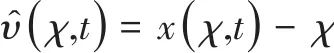 |
(5) |
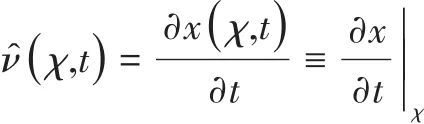 |
(6) |
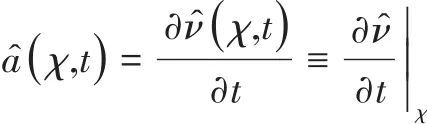 |
(7) |
利用链锁法则,可将物质速度表示为
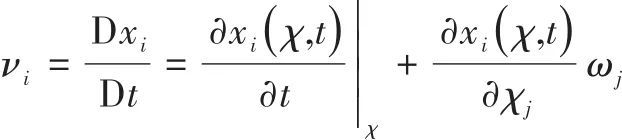 |
(8) |
式中右端第一项为![]() ,右端第二项中的
,右端第二项中的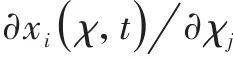 是映射
是映射![]() 的雅可比矩阵,它将质点的参考速度
的雅可比矩阵,它将质点的参考速度![]() 变化到空间坐标系中,将式(8)可进一步简化为
变化到空间坐标系中,将式(8)可进一步简化为
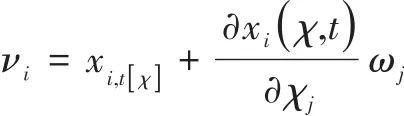 |
(9) |
式中下标中的“,t”表示对时间的导数,下标中的“[![]() ]”表示求导时
]”表示求导时![]() 不变。
不变。
利用式(8)将质点A相对于网格的速度cj(称为对流速度)表示为
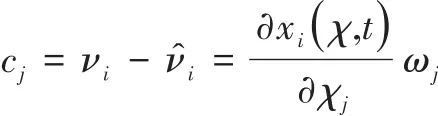 |
(10) |
所采用的ALE方程与传统Euler方程的唯一区别在于材料的导数项不同[26],ALE描述下的质量守恒方程为
 |
(11) |
式中![]() 表示密度,
表示密度,![]() 表示物质点的运动速度。
表示物质点的运动速度。
动量守恒方程为
 |
(12) |
式中![]() 为应力张量,
为应力张量,![]() 为单位质量体力向量。
为单位质量体力向量。
能量守恒方程为
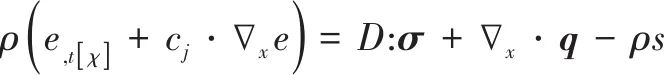 |
(13) |
式中e为单位质量内能,q为单位面积热流失量,![]() 为单位体积内的热源,D为变形率。
为单位体积内的热源,D为变形率。
边界条件满足
| (14) |
初始条件满足
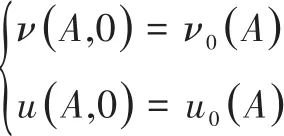 |
(15) |
2.3 基于ALE方法的刷式密封结构动力学有限元模型
刷丝作非线性运动的无量纲方程可以描述为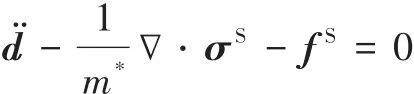 |
(16) |
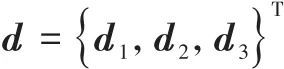 ,质量比
,质量比
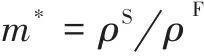 ,
,
 |
(17) |
式中![]() 是第二Piola-Kirchhoff应力,
是第二Piola-Kirchhoff应力,![]() 为弹性本构张量,
为弹性本构张量,![]() 表示Green-Lagrangian应变,
表示Green-Lagrangian应变,![]() 为变形梯度,I为单位矩阵。第二Piola-Kirchhoff应力经构形转换可表示为Cauchy应力
为变形梯度,I为单位矩阵。第二Piola-Kirchhoff应力经构形转换可表示为Cauchy应力
| (18) |
 |
(19) |
刷丝结构动力学有限元方程为
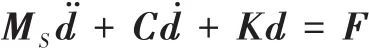 |
(20) |
式中![]() 为结构质量矩阵,
为结构质量矩阵,![]() 为阻尼矩阵,
为阻尼矩阵,![]() 为结构刚度矩阵,
为结构刚度矩阵,![]() 为外力向量。
为外力向量。
2.4 刷式密封ALE流固耦合方法
本文通过ANSYS Workbench数据交换平台建立LS-DYNA模块实现刷丝和流场的双向耦合。基于ALE流固耦合方法,采用罚函数耦合方式实现刷丝与流体之间的耦合作用,此方法有效地保证了流固耦合过程中的能量守恒[27]。当流体物质点“穿透”结构单元时,则根据两者的相对位移的大小分别对刷丝和流体施加相应的节点力,刷丝的动态响应与流场的压力和速度变化互相影响,进而生成新的网格。该算法在生成新的网格后会搜索新的流体物质点为下一循环耦合做准备。通过判断进出口泄漏量不再发生变化且相等,刷丝运动稳定时,则认为该计算过程收敛,Tn时刻循环结束,进入Tn+1循环时刻,否则将搜索新的流体物质点进行再循环。为防止穿过结构单元的流体质点未被搜索到,需要根据Lagrange和Euler单元的尺寸合理选择耦合点个数。耦合流程如图2所示。
Fig. 2 ALE fluid-structure interaction method analysis flowchart
03
刷式密封ALE流固耦合方法计算模型
3.1 求解模型
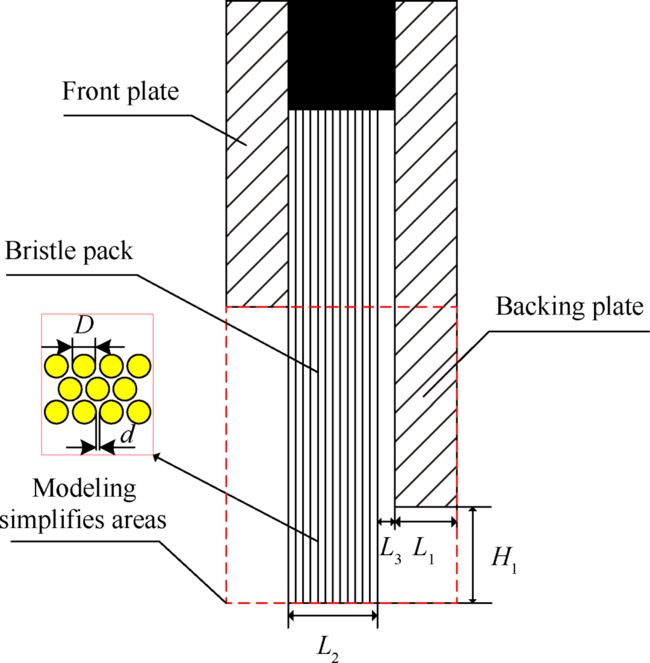
本文所设计加工的刷式密封件结构示意图如图3所示。该刷式密封结构主要结构参数如表1所示,刷丝束厚度为1.80mm,刷丝直径为0.80mm,刷丝与后挡板位置的轴向间隙0.5mm。刷丝材料为Haynes25,弹性模量为213.7GPa,泊松比0.29。在实际计算时选取前挡板以下区域,刷丝排数为20排,以最小周期循环单元建立模型,采取中间整排,两侧半排进行建模。
Fig. 3 Diagram of structure of brush seal experimental parts
Table 1 Brush seal main geometric dimensions3.2 网格划分
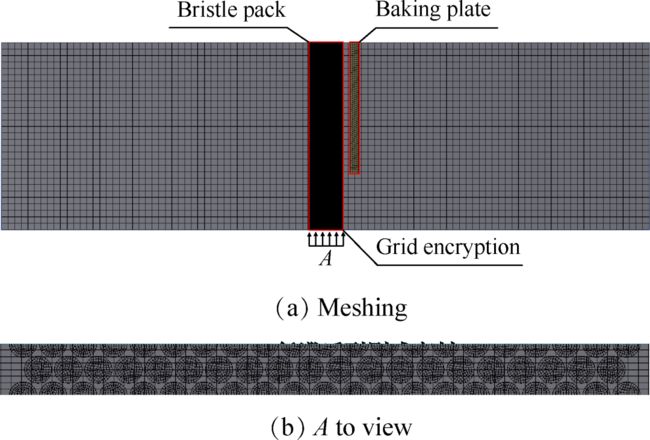
在进行网格划分时,为了提高网格质量及计算效率,流体域和刷丝区域均采用规则的六面体网格,并对刷丝束区域网格进行加密处理,网格划分如图4所示。在进行计算时考虑到网格质量对结果影响较大,对刷丝束区域采用网格加密处理,进行网格无关性验证,当网格数量达到327万时,泄漏量变化不超过5%,因此最终确定网格数量为327万。
Fig. 4 Meshing of brush seal
3.3 边界条件
在进行刷式密封流固耦合计算时,采用ALE算法对刷式密封进行求解。在刷式密封流固耦合模型中,采用压力入口和压力出口边界条件,采用对称面边界条件,其他边界为壁面边界条件。流固耦合的设置主要是通过关键字对流体与固体之间进行定义,流体与刷丝之间以及流体与挡板之间均为流固耦合边界条件,其中流体与刷丝束之间的耦合方式采用罚函数耦合方式,该耦合方式能够准确地计算刷丝变形条件下的流固耦合问题。边界条件示意图如图5所示,主要计算工况参数与边界条件如表2所示,其中刷丝间摩擦系数,刷丝与后挡板之间的摩擦系数均取0.3[28]。
Fig. 5 Brush seal boundary conditions
 Table 2 Main working condition parameters and boundary conditions
Table 2 Main working condition parameters and boundary conditions
04
刷式密封泄漏特性实验装置及原理
4.1 实验装置
本文设计搭建了刷式密封刷丝运动变形轨迹及泄漏特性实验装置,如图6(a)所示。该实验装置主要包括供气系统、密封系统、数据采集系统等,供气装置主要是通过空压机压缩空气,并储存在储气罐中,刷式密封实验件安装在密封腔室上,根据该密封腔室的结构特点,可通过轴向和径向来观测刷式密封刷丝运动变形轨迹,如图6(b)所示。进气腔可以有效稳定密封间隙上游区压力及流速,提高实验测量精度,压力传感器可测定密封进气口压力。数据采集系统主要由高速摄像机、涡街流量计、压力表、稳压电源和电脑等组成,为保证高速摄像机拍摄刷丝运动状态的清晰度,配有补光灯和放大镜,从而可以保证高速摄像机捕捉到清晰的刷丝运动轨迹,并储存在电脑中,为保证泄漏量实验精度,配有大小量程两个涡街流量计,记录仪可将流量数据转换为电信号及时储存在电脑内,保证了泄漏量的测量精度。
Fig. 6 Bristle deformation and leakage characteristics of brush seal test
4.2 实验原理
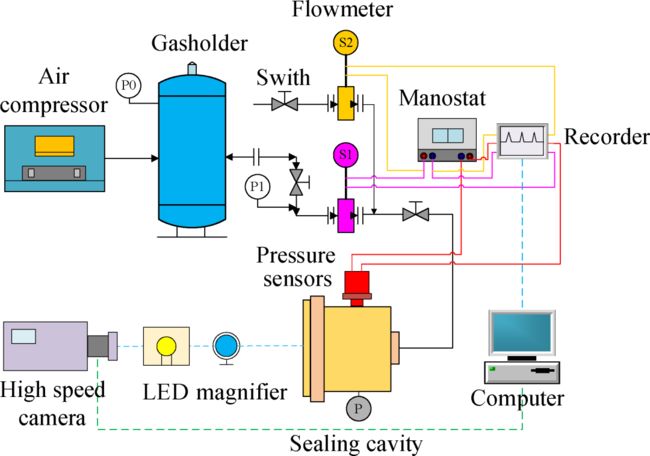
图7给出了刷式密封实验台气路示意图。空压机将压缩后的空气储存在储气罐中,最大可供压力为1.2MPa,可测不同压比条件下的刷式密封件的泄漏量,气流通过大量程涡街流量计(量程范围:110Nm3/h~870Nm3/h,精度等级:1.0级),在下游分支气路设有小量程流量计(量程范围:20Nm3/h~150Nm3/h,精度等级:1.0级),不同量程的涡街流量计可满足不同条件下的刷式密封泄漏量测量需求,以提高测量精度。当通过的流量较高时,可关闭小量程流量计上游的阀门,此时小量程涡街流量计读数为零,大量程涡街流量计读数即为对应压差下的流量;当流量较低时,以致大量程流量计的工况体积流量小于量程下限时,开启小量程流量计上游的阀门,此时,两流量计的流量差为测得的实验件流量。实验气缸上安装高精度压力传感器,来测量气缸内的压力,记录仪可将涡街流量计和压力传感器的实验数据转换为电信号实时显示并储存在电脑上,根据测试需求每秒可纪录多组数据,以保证实验数据的精度。刷式密封刷丝经过放大镜在高速摄像机中呈像,可实现刷式密封刷丝轴向和径向观测运动轨迹观测。
Fig. 7 Sealing test gas road
05
刷式密封实验与数值计算结果分析
5.1 刷式密封实验结果分析
5.1.1 刷丝运动状态对刷式密封泄漏特性影响分析
图8给出了在压比为2,刷丝自由端与转子面径向间隙为0mm条件下的刷式密封刷丝静止状态和工作状态刷丝吹下效应的实物照片。由于刷式密封存在着一定的周向倾角,气流经过刷丝束在后挡板的阻挡作用下,刷丝束所受径向力增大,在径向气流力作用下刷丝周向倾角改变,使得刷丝吹向转子,形成 “吹下效应”。由实验现象可知吹下效应主要发生在气流入口处的刷丝域,这是由于上游区刷丝受到的气流扰动较大,出口处刷丝由于受到更大的挤压力故不易产生较大范围的运动。由于吹下效应,刷丝束与转子之间的间隙减少,刷式密封泄漏量会减少。
Fig. 8 Bristle blow down of brush seal
图9给出了在压比为3,刷丝自由端与转子面径向间隙为0mm条件下的刷式密封刷丝静止状态和工作状态刷丝颤振实物照片。由实验现象可知前排刷丝更易出现刷丝颤振现象,这主要是因为前排位置刷丝受到气流扰动较大,非定常气动力对刷丝做功,刷丝吸收能量较多,容易出现颤振现象,而末排位置刷丝受到的气流力一部分被前排刷丝阻挡,受到气流扰动较少,相比前排刷丝运动较平稳。由于刷丝颤振现象导致刷丝丧失稳定性,甚至引起刷丝失效,造成刷丝与转子之间的间隙增大,流体在刷丝束中的有效流通面积增大,从而使得泄漏量增大。
Fig. 9 Bristle flutter of brush seal
图10给出了在压比为3,刷丝自由端与转子面径向间隙为0mm条件下的刷式密封刷丝静止与工作条件下的刷丝厚度的实物照片。由图中可以看出,刷式密封工作前后,刷丝束厚度发生了明显变化,这是因为在高速来流作用下刷式密封结构的刷丝运动趋势均由前挡板位置向后挡板位置运动,且刷丝与刷丝之间的间隙明显减少,刷丝排列更加密集,进而导致刷丝束密度增大。刷丝束密度增大可有效减少流体在刷丝束中的流通面积,使得密封性能增强,泄漏量减少。
Fig. 10 Changes of bristle thickness
5.1.2 刷式密封泄漏特性实验结果与数值验证
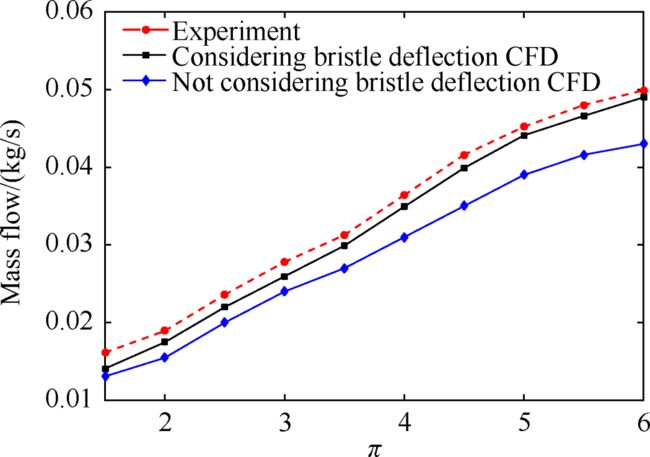
图11给出了不同压比下,刷丝自由端与转子表面的径向间隙为0mm时,实验测得无转速条件下与理论模型计算的刷丝运动稳定条件下泄漏量随压比π的变化曲线。此外旋转效应在一定程度上会影响刷式密封泄漏量,随着转速增大刷式密封泄漏量会略有减小[29]。本文研究了无转速条件下的刷式密封泄漏量随压比的变化规律。
Fig. 11 Comparison of experimental leakage with CFD results
由图中可以看出随着压比的增大,刷式密封泄漏量不断增大,考虑刷丝变形的数值计算值与实验测得泄漏量吻合较好,最大误差不超过5%,而未考虑刷丝变形的数值计算结果在低压比条件下吻合较好,随着压比的增大,误差逐渐增大,这是因为在实际工作中,刷式密封刷丝在气流力的作用下会发生变形,刷丝束由前挡板位置向后挡板位置移动,且压比越大,刷丝变形量越大,刷丝束厚也会发生变化,如图8至图10所示。因此未考虑刷丝变形的数值计算结果与实验值误差较大,而考虑刷丝变形的数值计算结果更接近实际刷丝运动情况,误差较小。
5.2 刷式密封流场特性和力学特性数值分析
5.2.1 刷式密封速度分布特性分析
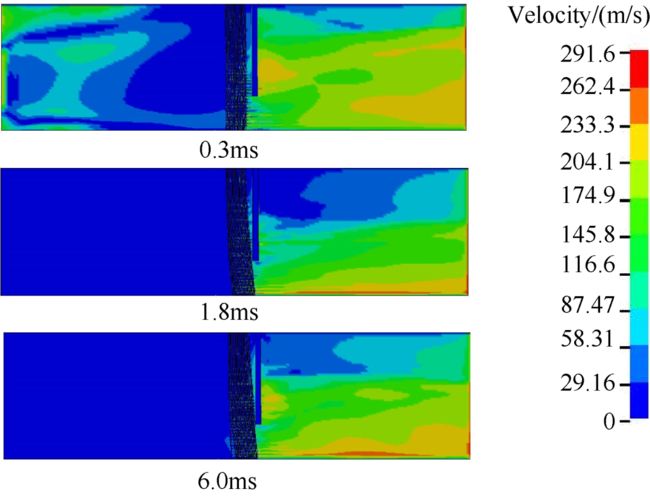
图12给出了不同时刻条件下刷式密封速度分布云图。由图中可以看出,在0.3ms时气流由进口经过刷丝束流向出口,此时气流未稳定,刷丝变形较小,气流速度较大;1.8ms时,气流逐渐趋于稳定,上游区速度较低,刷丝也发生了较大变形,末排刷丝发生弯曲且紧贴后挡板位置,最大速度出现在后挡板以下区域,经过刷丝束区域,下游区速度也发生了较大变化;当6ms时,气流基本稳定,气流速度不再发生明显变化,刷丝发生了较大变形,末排刷丝变形最大,最大速度出现在末排刷丝且靠近转子面位置。
Fig. 12 Velocity vector distribution with different times
5.2.2 刷式密封力学特性分析
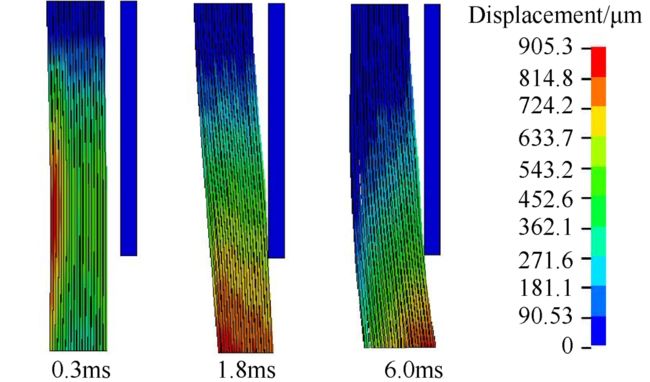
图13给出了刷式密封刷丝不同时刻的位移变形云图。由图中可以看出,在0.3ms时刷丝受到气流力作用,在刷丝固定端与自由端的前排刷丝首先发生变形,且刷丝之间间隙明显减小;在1.8ms时,刷丝发生了较大的弯曲变形,最大变形位置出现在刷丝自由端位置,且末排刷丝紧贴后挡板位置,刷丝根部变形量较小;在6ms时,刷丝变形量基本趋于稳定,紧贴后档板位置,由于刷丝与后挡板之间以及刷丝之间的碰撞,刷丝之间的间隙也发生了变化,最大变形位置出现在刷丝自由端位置,最大变形量为905μm。
Fig. 13 Bristle deformation with different times
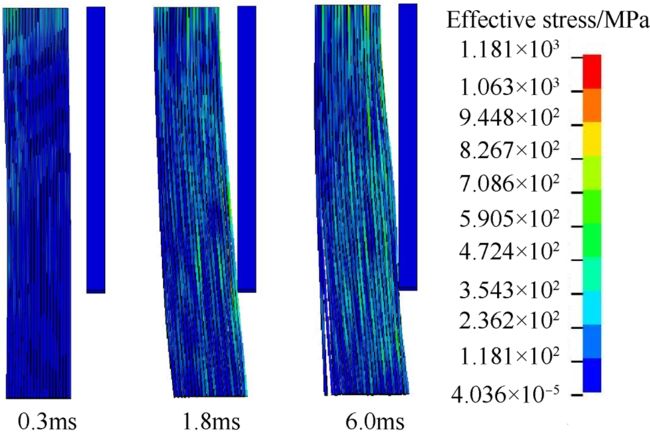
图14给出了不同时刻刷丝应力变化云图。由图中可以看出,在初始时刻刷丝最大应力出现在刷丝固定端和前排刷丝位置;随着时间的变化,当达到1.8ms时,刷丝变形逐渐增大,刷丝束贴向后挡板位置,刷丝应力范围也增大,这时末排刷丝与后挡板接触位置刷丝应力较大;当6.0ms时刷丝基本趋于稳定,此时刷丝变形量较大,刷丝束紧贴后挡板位置,刷丝束应力最大位置主要出现在刷丝固定端以及末排刷丝与后挡板接触位置。
Fig. 14 Bristle effective stress with different times
综上分析可知,在高速气流作用下,刷丝与刷丝之间会发生较大的接触碰撞和大变形,且末排刷丝与挡板之间也存在接触碰撞。本文采用基于ALE流固耦合方法对刷式密封进行数值研究,该方法具有较强的网格适应能力,自动剖分网格技术可解决刷丝大变形引起的负体积难题,能够实现刷丝接触碰撞和大变形的准确计算。
5.3 刷式密封泄漏特性影响分析
5.3.1 刷丝束自由端与转子面径向密封间隙对刷式密封泄漏量的影响分析
图15给出了径向密封间隙分别为0mm和0.2mm时的刷式密封泄漏量随压比的变化曲线。由图中可以看出,两种径向密封间隙的刷式密封泄漏量均随压比的增大而近似线性增大,在不同压比条件下,径向密封间隙0.2mm的刷式密封泄漏量明显高于径向密封间隙0mm的刷式密封泄漏量,两者相差51.6%~62.8%。可以看出径向密封间隙对刷式密封泄漏量有着重要影响,因此在实际工作中径向密封间隙不宜过大,否则会严重影响其密封性能。
Fig. 15 Effect of bristle radial clearance on leakege
5.3.2 刷丝排数对刷式密封泄漏量的影响分析
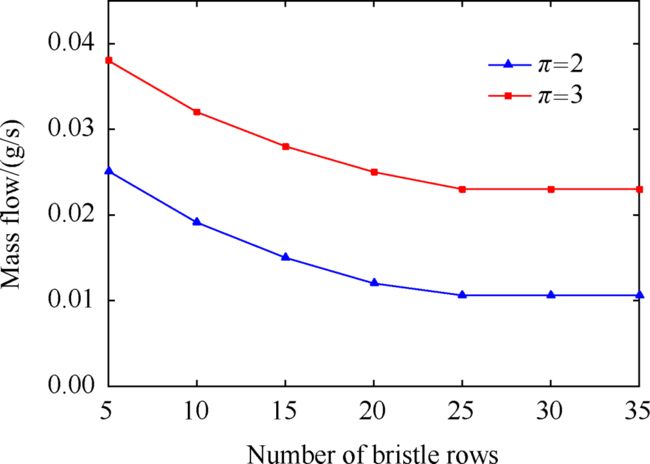
图16给出了在压比为2条件下,不同刷丝排数对刷式密封泄漏量的变形曲线。由图中可以看出,刷式密封泄漏量随着刷丝排数的增大而减少,后趋于稳定,这主要是因为随着刷丝排数的增多,气流力对刷丝做功,由于刷丝的阻碍作用,气流能量耗散增大,泄漏量减少。在相同刷丝排数情况下,进出口压比为3时的泄漏量明显大于进出口压比为2时的泄漏量,在两种压比条件下,当刷丝排数由5排增至20排时,刷式密封泄漏量明显减少,当增至25排时,刷式密封泄漏量变化趋于稳定,因此可知,当刷丝排数为25时,刷式密封泄漏量已达到理想状态,再增加刷丝排数对泄漏量影响不大。
Fig. 16 Effect of the number of bristle rows
5.3.3 刷丝间隙对刷式密封泄漏量的影响分析
图16给出了在压比为2条件下,不同刷丝排数对刷式密封泄漏量的变形曲线。由图中可以看出,刷式密封泄漏量随着刷丝排数的增大而减少,后趋于稳定,这主要是因为随着刷丝排数的增多,气流力对刷丝做功,由于刷丝的阻碍作用,气流能量耗散增大,泄漏量减少。在相同刷丝排数情况下,进出口压比为3时的泄漏量明显大于进出口压比为2时的泄漏量,在两种压比条件下,当刷丝排数由5排增至20排时,刷式密封泄漏量明显减少,当增至25排时,刷式密封泄漏量变化趋于稳定,因此可知,当刷丝排数为25时,刷式密封泄漏量已达到理想状态,再增加刷丝排数对泄漏量影响不大。
Fig. 16 Effect of the number of bristle rows
5.3.4 末排刷丝与后挡板间的轴向间隙对刷式密封泄漏量的影响分析
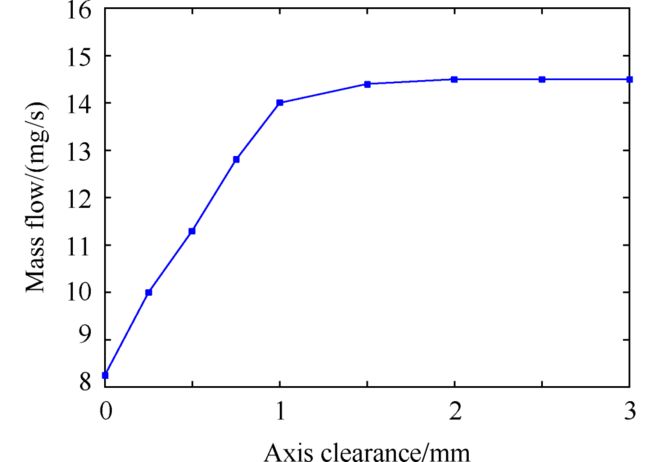
图18给出了在压比为2条件下,刷式密封泄漏量随轴向间隙的变化曲线。由图中可以看出,泄漏量随着轴向间隙的增大先逐渐增大后趋于稳定,当轴向间隙从0mm增加至1.5mm时,泄漏量明显增大,当轴向间隙大于1.5mm时,泄漏量变化不大,趋于稳定。这主要是因为当末排刷丝与后档板之间的轴向间隙较小时,刷丝在气流力作用下紧贴后挡板,后挡板能够有效地阻碍刷丝变形,减少泄漏,当末排刷丝与后挡板距离较大时,在气流力作用下,刷丝向后挡板方向移动,刷丝变形量增大,从而导致泄漏量增大。因此,减少后挡板保护高度能够有效地减小泄漏量。
Fig. 18 Effect of axial clearance of backing plate
5.3.5 后挡板保护高度对刷式密封泄漏量的影响分析
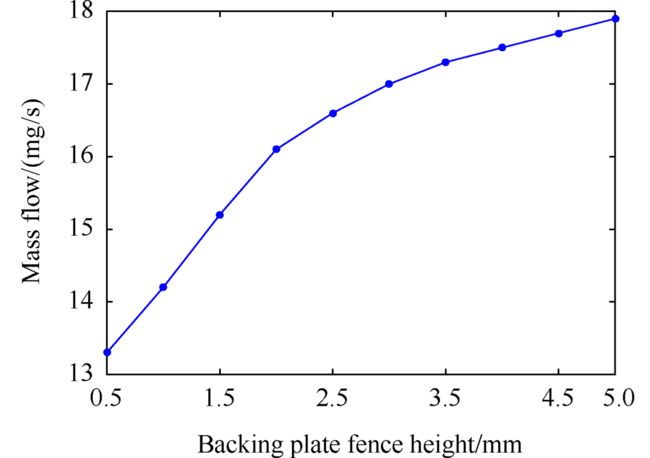
图19给出了在压比为2条件下,后挡板保护高度对泄漏量的变化曲线。由图中可以看出,当后挡板保护高度从0.5mm增至5mm时,泄漏量不断增大,且逐渐趋于平缓。这主要是因为随着后挡板保护高度的增加,后挡板对刷丝变形的阻碍作用减弱,对气流的阻碍作用减弱,导致泄漏量逐渐增大,当增大到一定高度时,在该工况条件下,刷丝的变形量逐渐趋于稳定,从而使得泄漏量变化趋于平缓。
Fig. 19 Effect of height of backing plate fence
06
结论
通过本文研究,得到以下结论:
(1)本文提出的基于ALE流固耦合方法的考虑刷丝变形接触的刷式密封求解模型,解决了传统刷式密封求解模型因刷丝接触导致网格畸变而难以计算的问题,可准确计算刷式密封流场特性和力学特性。
(2)刷式密封刷丝吹下效应和刷丝颤振现象主要发生在气流入口处的前排刷丝域,吹下效应使得刷式密封泄漏量降低,刷丝颤振会导致泄漏量增大;在气流力作用下,刷丝束轴向厚度变小,泄漏量减小。
(3)在本文研究模型条件下,在气流力作用下,刷丝固定端与自由端的中间部位先发生变形,最大应力出现在刷丝固定端和前排刷丝位置,随着气流速度逐渐趋于稳定,最大变形位置出现在刷丝自由端,而刷丝固定端、末排刷丝与后挡板接触位置应力较大。
(4)刷式密封泄漏量随着径向密封间隙的增大而增大,在本文所研究工况条件下,径向密封间隙为0mm与0.2mm时的泄漏量相差51.6%~62.8%;随着刷丝排数的增大,泄漏量逐渐减小,当刷丝排数大于25排时,其对泄漏量影响较小;随着刷丝间隙、刷丝与后挡板之间的轴向间隙、后挡板保护高度的增大,泄漏量先逐渐增大后趋于平缓。
在下一步的研究工作中,将会开展旋转效应对刷式密封泄漏特性影响规律的理论与实验研究。参考资料:
1. 李 军, 晏 鑫, 宋立明, 等. 透平机械密封技术研究进展[J]. 热力透平, 2008, 37(3): 141-148. 2. Steinetz B M, Hendricks R C. Advanced Seal Technology in Meeting Next Generation Turbine Engine Goal[R]. NASA/TM-1998-06961. 3. 李 军, 李志刚, 张元桥, 等. 刷式密封技术的研究进展[J]. 航空发动机, 2019, 45(2): 74-84. 4. Bayley F J, Long C A. A Combined Experimental and Theoretical Study of Flow and Pressure Distributions in a Brush Seal[C]. New York:37th International Gas Turbine and Aeroengine Congress and Exposition, 1993: 404-410. 5. Chew J W, Lapworth B L, Millener P J. Mathematical Modeling of Brush Seals[J]. International Journal of Heat & Fluid Flow, 1995, 16(6): 493-500. 6. Chew J W, Hogg S I. Porosity Modeling of Brush Seals[J]. ASME Journal of Tribology, 1997, 119(4): 769-775. 7. 王之栎, 梁小峰, 宋 飞, 等. 低滞后刷式密封数值分析[J]. 北京航空航天大学学报, 2008, 34(9): 1080-1083. 8. 丁水汀, 陶 智, 徐国强. 刷式封严流动和换热的数值模拟[J]. 推进技术, 1999, 20(1): 65-67.( DING Shui-ting, TAO Zhi, XU Guo-qiang. Numerical Simulation on Fluid Flow and Heat Transfer of a Brush Seal Configuration[J]. Journal of Propulsion Technology, 1999, 20(1): 65-67.) 9. 黄学民, 史 伟, 王洪铭. 刷式密封中泄漏流动的多孔介质数值模型[J]. 航空动力学报, 2000, 15(1): 55-58. 10. 邱 波, 李 军. 刷式密封传热特性研究[J]. 西安交通大学学报, 2011, 45(9): 94-100. 11. 张元桥, 王 妍, 晏 鑫, 等. 刷式密封泄漏流动及传热特性的研究第二部分: 传热特性[J]. 工程热物理学报, 2018, 39(5): 970-976. 12. 张元桥, 闫嘉超, 李 军. 刷式密封泄漏和传热特性影响因素的数值研究[J]. 推进技术, 2018, 39(1): 116-124.( ZHANG Yuan-qiao, YAN Jia-chao, LI Jun, et al. Numerical Investigations on Influence Factors of Leakage Flow and Heat Transfer Characteristics of Brush Seal[J]. Journal of Propulsion Technology, 2018, 39(1): 116-124.) 13. 孙 丹, 刘宁宁, 胡广阳, 等. 考虑刷丝变形的刷式密封流场特性与力学特性流固耦合研究[J]. 航空动力学报, 2016, 31(10): 2544-2553. 14. 孙 丹, 白伟钢, 刘宁宁, 等. 基于能量法的刷式密封刷丝颤振流固耦合研究[J]. 推进技术, 2018, 39(3): 619-629.( SUN Dan, BAI Wei-gang, LIU Ning-ning, et al. Fluid-Solid Interaction Study of Brush Seals Bristle Flutter with Energy Method[J]. Journal of Propulsion Technology, 2018, 39(3): 619-629.) 15. 宗兆科. 动压式指尖密封工作状态及其影响的流固耦合分析[J]. 航空动力学报, 2010, 25(9): 2156-2162. 16. 白花蕾, 吉洪湖, 曹广州. 指尖密封泄漏特性的实验研究[J]. 航空动力学报, 2009, 24(3): 532-535. 17. 刘占生, 叶建槐. 刷式密封接触动力学特性研究[J]. 航空动力学报, 2002, 17(5): 635-640. 18. Ferguson J G. Brushes as High Performance Gas Turbine Seals[C]. New York: International Gas Turbine & Aeroengine Congress & Exposition, 1988. 19. Bayley F J, Long C A. A Combined Experimental and Theoretical Study of Flow and Pressure Distributions in a Brush Seal[C]. New York:International Gas Turbine & Aeroengine Congress & Exposition, 1993. 20. Turner M T, Chew J W, Long C A. Experimental Investigation and Mathematical Modeling of Clearance Brush Seals[J]. ASME Journal of Engineering for Gas Turbines and Power, 1998, 120(3): 573-579. 21. Chupp R E, Dowler C A. Performance Characteristics of Brush Seals for Limited-Life Engines[J]. ASME Journal of Engineering for Gas Turbines and Power, 1993, 115(2): 390-396. 22. 孙晓萍. 刷式密封性能和耐久性试验研究[J]. 航空发动机, 2002, 28(3): 37-41. 23. 曹广州, 吉洪湖, 纪国剑. 刷式封严初期使用特性的实验和数值研究[J]. 推进技术, 2010, 31(4): 478-482.( CAO Guang-zhou, JI Hong-hu, JI Guo-jian. Experimental and Numerical Study on the Leakage Characteristics of Brush Seals at the Early Stage of Operating[J]. Journal of Propulsion Technology, 2010, 31(4): 478-482.) 24. 胡广阳, 孙 丹, 刘宁宁, 等. 刷式密封泄漏及磨损特性实验研究[J]. 沈阳航空航天大学学报, 2016, 33(2): 1-5. 25. 杜春华, 吉洪湖, 胡娅萍, 等. 刷式封严磨损特性及其对泄漏影响的试验研究[J]. 推进技术, 2017, 38(11): 202-210.( DU Chun-hua, JI Hong-hu, HU Ya-ping, et al. Experimental Investigation on Wearing Characteristics and Effects on Leakage of Brush Seal[J]. Journal of Propulsion Technology, 2017, 38(11): 202-210.) 26. 王 学. 基于ALE方法求解流固耦合问题[D]. 长沙:国防科学技术大学, 2006. 27. 张伟伟, 金先龙. 球体撞击自由液面相关效应的数值模拟方法研究[J]. 船舶力学, 2014, 18(1): 28-36. 28. Fellenstein J, Dellacorte C, Moore K, et al. High Temperature Brush Seal Tuft Gesting of Selected Nickel-chrome and Cobalt-Chrome Superalloys[R]. AIAA 97-2634. 29. 张元桥, 闫嘉超, 李 军. 考虑闭合效应的刷式密封泄漏特性研究[J]. 润滑与密封, 2017, 42(4): 36-42来源|推进技术
作者|李国勤
· end ·