【DeepLearning学习笔记】Neurons神经元
今天找到一个比较好的deep learning的教材:Neural Networks and Deep Learning 对神经网络有详细的讲解,鉴于自己青年痴呆,还是总结下笔记吧=。=
Perceptron感知器
Perceptron的输入的一组binary变量xi,对这些binary变量求出加权和后,如果这个和大于某个阈值threshold,就输出1;否则输出0.
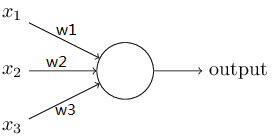
所以perceptron的输入输出都是binary的,我们可以把一个perceptron的输入看成一组“evidences”(证据),perceptron利用这组证据判断出一个decision(决策)。
比如说我们用一个perceptron判断一个女生会不会买一双鞋,就用上图的perceptron,假设这个女生有三个评价标准:
x1:这双鞋是否打折?
x2:这双鞋小伙伴们是否还没有?
x3:这双鞋是否是今年新款?
以上各个变量如果回答是“是”,则对应xi为1,否则为0.并且假设threshold为3,即如果w1x1+w2x2+w3x3≥3,那么输出1,否则输出0.
第一种情况:这个女生非常(chu)挑(nv)剔(zuo),她要求这三个评价标准都满足,才会买这双鞋,这时可以设置w1=w2=w3=1,那么只有x1=x2=x3的时候,perceptron的输出才是1,否则是0.
第二种情况:这个女生非常自(jiao)主(qing),她很讨厌和别人买一样的鞋,那么第二个标准对她非常重要,而其他两个都不重要。这是可以设置w2=3,w1=w3=1,那么只有当x2=1的时候perceptron才可能输出1,否则不管x1和x2取什么值,perceptron都只输出0.
以上是perceptron的直观理解,以下是数学表示:
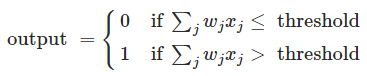
这个表示有两坨东西非常复杂,一个是求和符号,另一个是threshold。那么为了简化,我们可以利用向量运算代替求和符号,即∑wjxj = wx,其中w是权重向量,x是样本向量。另外设置一个变量b=-threshold,然后把它挪到不等号左边,那么上述数学表示就变成了:
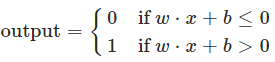
所以一个perceptron所做的工作就是把所有输入和它们对应的权重相乘求和后加上偏置b然后和0比较,大于0输出1,小于0输出0.
Sigmoid神经元
在神经网络的训练过程中,我们随机初始化权重,然后通过训练数据逐步的修改权重,使得神经网络最终能够完成某项任务。上述的perceptron有一个缺点就是如果它的某一个权重发生了细微的变化,那么output的值很有可能直接从0跳变到1,并且它的输出跳变就有可能引起更大范围的不可控的跳变,这样我们就不能“逐(ping)渐(wen)”的调整网络的权重来训练网络。
这个时候就要引入sigmoid神经元了。它的结构和上述perceptron是十分相似的,同样有若干个输入xi,对应若干个权重wi,一个输出output。不过这些x以及output都是[0,1]之间的实数了,而不限定与binary了。并且,sigmoid神经元的工作要比perceptron稍微复杂一些:当这个perceptron把输入x和权重求完加权和后,并不是用threshold来判断输出,而是将这个加权和作为sigmoid函数(f(x)=1/(1+exp(-x)))的输入,最后函数值作为输出。
为什么这个函数可以解决perceptron的问题呢?因为如下这个公式:
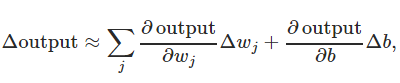
假设我们在训练网络的时候对w的修改是Δw,对b的修改是Δb,那么输出的变化是Δw和Δb的线性和(上述偏导都可以看成线性关系的系数),也就是说Δoutput=∑aiwi+bΔb(a,b都是偏导),这样一来,Δw和Δb微小的变化就不会引起output的突然跳变,而是一个线性缓慢变化的过程,这样我们训练神经网络的过程就可控了。
sigmoid的输出和perceptron是相似的,从它们的图像就可以看出来:
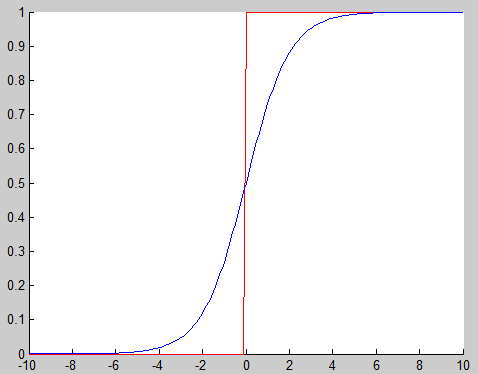
红色的是perceptron,蓝色是sigmoid。二者均是当输入接近正无穷时输出接近1;当输入接近负无穷时,输出接近0.只是在0附近,perceptron的函数是跳变,而sigmoid是逐渐变化,正是这种逐渐变化使得sigmoid可导并且权重的微小变化引起的输出的变化是可控的,而不是跳变。
所以sigmoid函数重要的是它的形状好,其实这个形状的还有tanh正切函数(输出在[-1,1]而不是(0,1)):
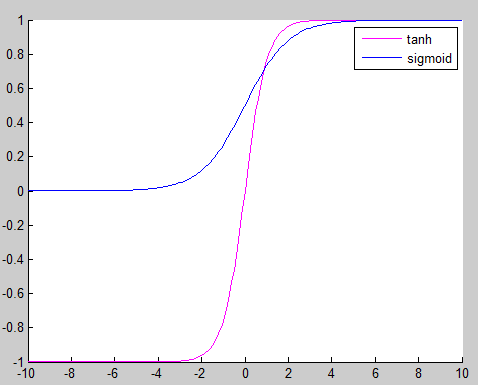
那么为什么sigmoid使用更广泛呢?因为它有一个极好的求导性质:
f(z)=1/(1+exp(-z))
f'(z)=f(z)(1-f(z))
这个性质在训练神经网络的BP算法中使我们可以快速计算sigmoid函数的梯度,所以sigmoid函数在神经网络中使用更广泛。