LeetCode-4-寻找两个有序数组的中位数
题目
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/median-of-two-sorted-arrays
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
标签: 数组、分治算法、二分查找
解题思路
- 首先第一种暴力解法, 就是将两个数组合并再取中位数; 但是这样的时间复杂度再合并阶段就达到了
O(m+n)显然不符合要求 - 第二种解法是类似于归并排序中的合并, 但是也是
O(m+n)的时间复杂度
第三种解法
这是从LeetCode中看到的, 在这里分析并用C++实现, 侵权删!
- 求中位数, 其实也就是求指定第
k位数 - 归并排序中的合并步骤, 是把两个数组中的数每次一位按顺序的放入合并后的有序数组, 每一步可以获得第
+1顺序的数. - 那么优化后的算法就是一次
合并多位, 我们仅需考虑第k位的数; 前面和后面并不需要有序
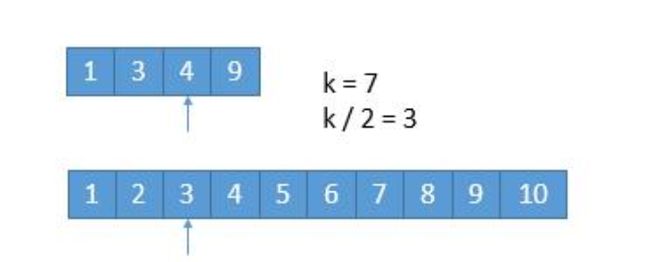
那么如图, 当我们尽可能的想移动多位的话, 那么应当移动多少位? 毫无疑问是: k/2位.
原因是: 因为移动多位可能移动上下两个数组的任意一个, 而 N1[k/2]或N2[k/2]中小的那一个不会超过N[k](合并后的坐标); 那么我们移动k/2较小的一部分那么必然不会超出.
-
我们考虑奇数和偶数的情况
- 奇数: k = (n+m+1)/2
- 偶数: k = (n+m)/2 和 k = (n+m+2)/2
- 我们需要注意的是:
n+m是奇数的话(n+m+1)/2=(n+m+2)/2; 如果n+m是偶数的话(n+m)/2=(n+m+1)/2 - 所以我们需要求取的是:
(n+m+1)/2和(m+n+2)/2的值, 最后除以2
最后就是使用递归实现了, 更简洁
C++实现
class Solution {
public:
double findMedianSortedArrays(vector& nums1, vector& nums2) {
int m = nums1.size();
int n = nums2.size();
return (getKth(nums1, 0, m-1, nums2, 0, n-1, (n+m+1)/2)+getKth(nums1, 0, m-1, nums2, 0, n-1, (n+m+2)/2))*0.5;
}
double getKth(vector& nums1, int l1, int r1, vector& nums2, int l2, int r2, int k)
{
int len1 = r1 - l1 + 1;
int len2 = r2 - l2 + 1;
if(len1 == 0) return nums2[l2+k-1];
if(len2 == 0) return nums1[l1+k-1];
if(k == 1) return min(nums1[l1], nums2[l2]);
int i = min(len1, k / 2) - 1 + l1;
int j = min(len2, k / 2) - 1 + l2;
if(nums1[i] < nums2[j])
return getKth(nums1, i+1, r1, nums2, l2, r2, k-(i-l1+1));
else
return getKth(nums1, l1, r1, nums2, j+1, r2, k - (j-l2+1));
}
};