关于计算机网络海明Hamming Code校验码, CRC及奇偶码校验
关于计算机网络Hamming Code海明校验码, CRC及奇偶码校验
-
- Abstract
- 奇偶校验码 parity check code
- 冗余校验码Cyclic Redundancy Check
- 海明校验码Hamming code
- Conclusion
- Reference
Abstract
在数字化通信系统里面,数据的传输应该保持无错误及高精准度,由于数据错误经常导致丢失一些重要的安全数据,因此为了更好地克服这个问题,我们该如何进行报文传送的过程中进行错误检测和纠错,同时我们如何对传输的信息进行有效加密,比如电子签名,值得我们思考。笔者通过这篇文章主要阐明海明Hamming Code校验码, CRC及奇偶码带来哪些好处及之间的区别及让我们进一步思考为什么海明码添加奇偶校验码能成为一种较理想的校验码。
奇偶校验码 parity check code
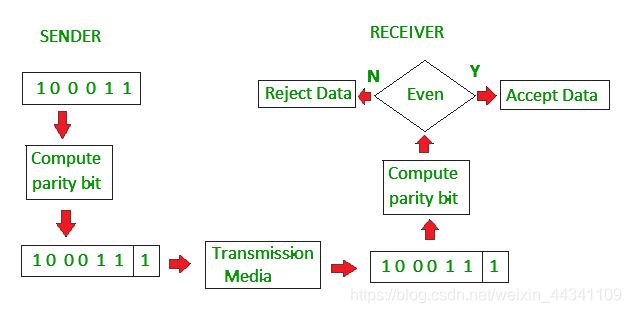
什么是奇偶校验?
奇偶校验是确保两个端点之间通信时数据准确传输,是通过拼接一个位到原始数据创造一个奇偶位数字,这些数据通过链路传输,并且在目的端进行位检测和验证,如果奇偶位是匹配的说明数据是准确的。例如,如果原始数据是1010001,这里有三个 1s,当使用偶校验时,一位奇偶位添加到数据的最左边使 1s数量变成偶数,此时传输数据变成了11010001。然而,如果使用奇数时,奇偶位变成了 0,即 01010001。如果原始数据包含的 1s数量是偶数,则添加一位 1 奇偶位到最左边使得1s数量变成奇数,如果使用的是奇数奇偶检测,则传输的数据变成了 11101001。接受端与发送端达成一致协议使用一样的奇偶位检测方法,即要么是奇数或偶数。如果这个协议没有配置成功,则无法进行数据通信。一旦数据传送到了接收端,如果此时数据是不正确的,则奇偶值也就变成了错误的,因此表明数据传输的过程中出现了错误。
奇偶检测应用在数据通信,比如作为使用为内存存储设备测试,当数据被读取时进行内存检测。它是一种能检测单个错误的基本方法,但是无法检测,比如由电子噪声干扰而造成的位改变数量,事实上,如果噪声干扰后接收端和发送端将都是错误的,两者都得到了补偿。尽管这些发生的机会是很遥远的,但在一个大型的计算机系统,确保数据的完整性是基本需要,因此一个第三方位可以分配为奇偶检测。
独立磁盘的随机阵列Redundant array of independent disks (RAID) 也使用了一个基于奇偶的保护加强形式,检查横行和纵向奇偶性。为了避免发生错误时数据丢失,所有的驱动将写入了第二组奇偶校验数据。当 RAID 驱动奇偶检测失败了,数据将使用奇偶信息耦合其他磁盘数据进行重建。其余驱动上的位将会累加,当增加到一个奇数数字时,此时失败驱动上的纠错信息将变成了偶数,反之亦然。 如下是两种形式奇偶位:
-
偶校验位
如果一个给定的二进制数据上的 1s 数量加起来是奇数时,则奇偶位的值设置为 1,使最终总共出现的 1s 数量加起来时一个偶数。如果在一个给定的二进制数据上 1s 数量加起来是偶数时,则奇偶位的值设置为 0。 -
奇校验位
如果一个给定的二进制数据上的 1s 数量加起来是偶数时,则奇偶位的值设置为 1,使最终总共出现的 1s 数量加起来时一个奇数。如果在一个给定的二进制数据上 1s 数量加起来是奇数时,则奇偶位的值设置为 0。
什么是2D矩阵奇偶校验?
假设一个单一的位错误出现在原始数据 d 位上,利用二维奇偶校验方案,出现错误的位将呈现在纵向和横向交叉位置上,因此接受端不仅仅检测到原始数据出现了1 位错误,而且能依据二维矩阵准确定位到出现错误的位置,如下图位错误值位 0 出现在(1,1)位置。
接收端能同时检测和纠错叫做forward error correction (FEC)正向纠错,这个技术通常使用在音频存储和播放设备比如音频CD,FEC正向纠错可以有效减少重传数据。同时,最重要的是FEC能满足接收端即时纠错,能有效避免等待传播时延。
冗余校验码Cyclic Redundancy Check
CRC 冗余校验码是一种基本的数据校验方法,用于检验磁盘数据的准确性,CRC 能检测原数据偶尔发生改变。CRC错误出现主要是由于硬盘毁坏,文件错误配置,磁盘凌乱,程序安装不成功,或在出现媒介斑点时。CRC错误也可能会导致系统错误或数据丢失,因此必须得到解决。
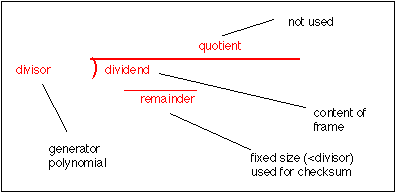
CRC 实际上是在数据信息后面添加几位冗余码构成k+n 数据帧发送出去,接受端接受到数据后重新计算CRC,并且比较计算的结果,如果两者之间的值不相同,则说明出现错误。CRC计算首先给一个16位的寄存器全部预加载数字1,然后进程开始加载报文的后面8位到寄存器的当前内容,仅仅每一个字符串里的8位用于产生CRC,首尾及奇偶位不参与到CRC运算。
- 计算CRC,例如我们使用3位CRC 多项式x^3 + x + 1来编码14位的报文,这个多项式以二进制表示作为公因子,一个3次项的多项式有4个公因子(1, 0, 1 and 1)如下:
- k+1 位检查序列发生器等于k次多项式 x³ + x + 1
- 报文加上k个 0, 为 11010011101100 000
11010011101100 000 <— input right padded by 3 bits
1011 <— divisor (4 bits) = x³ + x + 1
01100011101100 000 <— result
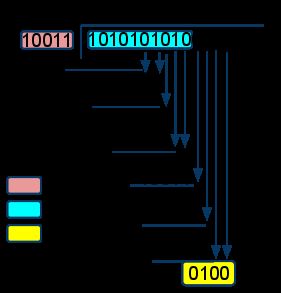
例如:
G(x) = 10011 = x ^ 5 + x ^ 1 + 1
D(x) = 10 1010 1010 = x ^ 10 + x ^ 8 + x ^ 6 + x ^ 4 + x ^ 2
R(x) = 0100 (remainder)
常用的三种多项式如下:
CRC-16 = x16 + x15 + x2+ 1 (used in High-level Data Link Control Protocol - HDLC)
CRC-CCITT = x16 + x12 + x5 + 1
CRC-32 = x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 (used in Ethernet)
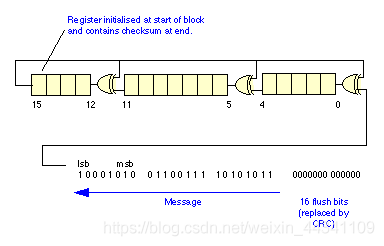
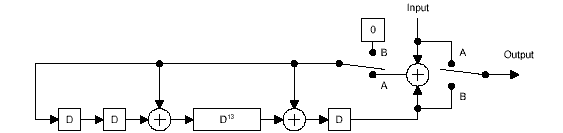
如图:一个解码器的具体实现,在传输数据帧的第1位之前需要初始化解码器,并且在发送完最后一位数据后需要冲刷解码器。具体实现工作原理如下图,首先通过设置开关到B位置进行全部赋0初始化,然后开关移动到A位置并且每一个时钟周期进入一个数据位,在最后一位发送完成后,开关再返回到B位置,并且解码器的内容随之从output 发送出去。这个具体实现叫做冲刷解码器并且需要位移寄存器每一个时钟周期携带1位数据。另外在接受端,这个实现过程正好相反,如果CRC包含了0(初始化赋予为0),说明CRC是有效的,如果不是则说明检测到了一个错误。同时CRC-16能检测到所有的单个错误和二重错误及所有的奇数错误和所有长度小于16位的突发错误。
CRC是特别设计用于保护通信信道可能出现的一些常见错误,可以用于快速及合理保证传递到的数据完整性,但是无法用于保护恶意更改的数据。
- 由于CRC没有认证,一名黑客可以编辑报文及重新计算CRC并且无法检测到已经被替换,即使利用hash 算法也无法得到有效保护。不过,任何要求得到安全保护的应用都必须要使用密码认证机制,比如短信认证CRC码或电子签名(普遍基于加密hash 算法);
- 不像加密hash 算法,CRC是一个相对容易的可逆函数,因此不太适用于在电子签名;
- CRC是一个线性函数,即使采用流密码加密,使用异或门作为组合(或使用能转化成流密文的分组密码模式,比如OFB or CFB),短信验证或关联CRC的两者都可在不知道加密密钥的情况下进行操纵,这就是有线等效加密协议Wired Equivalent Privacy (WEP)其中著名的设计缺陷之一。
海明校验码Hamming code
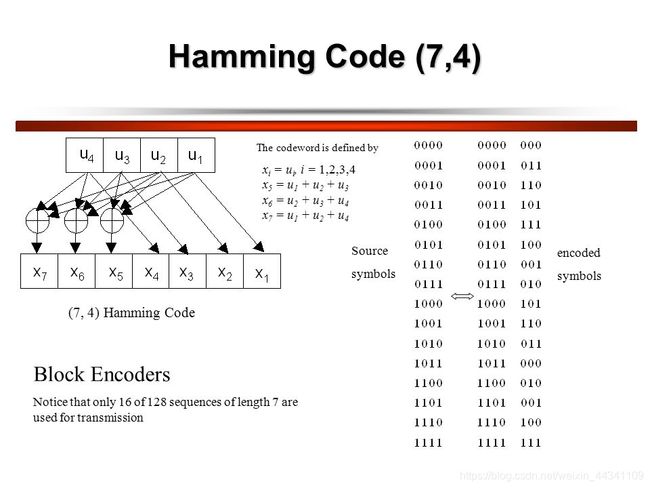
在计算机科学和通信学里,海明码Hamming code 是线性纠错码的成员之一,是一种理想的校验码,可以用于检测和纠错发送端到接受端传输数据时发生的错误,可检测2位以上错误及在未检测到无法纠正错误时可以纠正1位错误,是由 R.W. Hamming 于1950年发明的一种数据纠错方式。冗余位是附加的二进制位数,用于添加到传送数据位上确保数据传送期间无数据丢失。冗余位的数量可以使用以下公式计算:
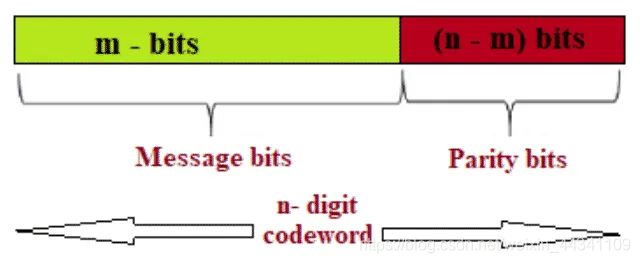
海明校验码Hamming code的结构如下图,整个的数据流长度由报文位数叫做数据位(m)和奇偶位 (n-m)组成,因此整个密码字的长度为[m+(n-m)].
2^r ≥ m + r + 1
where, r = redundant bit, m = data bit
假设数据位是7位,可以如下计算
= 2^4 ≥ 7 + 4 + 1
因此,冗余位的数量是 = 4位
| Position | R8 | R4 | R2 | R1 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
海明码Hamming Code是如何进行工作的?
使用海明码进行错误检测和纠正的原理时依据它的海明距离,异或运算也称作模加法,对第二个数据字符串进行模加法,并且对 1s 的数量累加。

计算海明码的关键是使用额外的校验位去鉴别某一个单一的错误。具体如下:
- 以2的倍数标记所有的位置作为校验位,比如1, 2, 4, 8, 16, 32, 64, etc.
- 所有的其他位用于数据编码,比如3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc.
- 校验位的位置决定校验和跳跃的位置序列
- 位置 1: 检查1位,跳过1位,检查1位,跳过1位,等(1,3,5,7,9,11,13,15,…)
- 位置 2: 检查2位,跳过2位,检查2位,跳过2位,等(2,3,6,7,10,11,14,15,…)
- 位置 4: 检查4位,跳过4位,检查4位,跳过4位,等(4,5,6,7,12,13,14,15,20,21,22,23,…)
- 位置 8: 检查8位,跳过8位,检查8位,跳过8位,等(8-15,24-31,40-47,…)
- 位置 16: 检查16位,跳过16位,检查16位,跳过16位,等(16-31,48-63,80-95,…)
- 位置 32: 检查32位,跳过32位,检查32位,跳过32位,等(32-63,96-127,160-191,…)
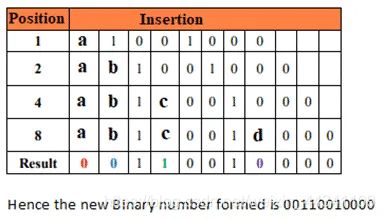
如果它的检测位置上 ‘1’ 的数量为奇数,则设置一个奇偶检测位为1,如果它的检测位置上 ‘0’ 的数量为偶数,则设置一个奇偶检测位为0.例如:
- 数据包:10011010
- 创建一个留空间的数据位:_ _ 1 _ 0 0 1 _ 1 0 1 0
- 对每一个奇偶位计算它的奇偶性(?代表位置被设置)
- 位置1检查1,3,5,7,9,11: ? _ 1 _ 0 0 1 _ 1 0 1 0. 为偶数所以设置位置1为 0: 0 _ 1 _ 0 0 1 _ 1 0 1 0
- 位置2检查2,3,6,7,10,11:0 ? 1 _ 0 0 1 _ 1 0 1 0. 为奇数所以设置位置2为1: 0 1 1 _ 0 0 1 _ 1 0 1 0
- 位置4检查4,5,6,7,12: 0 1 1 ? 0 0 1 _ 1 0 1 0. 为奇数所以设置位置4为1: 0 1 1 1 0 0 1 _ 1 0 1 0
- 位置8检查8,9,10,11,12: 0 1 1 1 0 0 1 ? 1 0 1 0. 为偶数所以设置位置8为0: 0 1 1 1 0 0 1 0 1 0 1 0
- 码字为:011100101010
- 然后找到并修复一个问题位,如下:
- 以上创建的码字为 011100101010,此时假设接受到的码字为 011100101110. 然后计算接受到的码字哪一个位是错误的并纠正它;
- 可以发现奇偶位2 和 8 时错误的,并且 2+8 = 10, 则位置10上是一个错误点;
- 总体上就是检查每一个奇偶位,然后把错误的位置加起来,然后相加的结果就是问题点的位置。
因此我们选择 CB 为 4, 然后这些位添加到原始数据叫做奇偶校验位,最终 Bit Length (7) + Parity Bits (4) = Encrypted Data (11 bits)
因此,我们得到的新的二进制数据是 00110010000
海明码Hamming Code的主要应用:
海明码Hamming Code的优势:
- 用于检测和纠错非常高效
- 在数据流网络上使用海明码Hamming Code纠错单个位错误时非常高效
海明码Hamming Code的劣势:
- 带宽将会增加
- 额外的奇偶位的增加将下降传输效率
Conclusion
- 奇偶校验码 Parity bits 采用位拼接到一个二进制位的数据的方式来确保最终整个数据中 1s 的数量是奇数还是偶数,用于错误检测,也通常用于捆绑在海明码进行使用。
- 冗余校验码Cyclic Redundancy Check (CRC) 使用校验和作为多项式除法结果,是一种确保数据传输过程中能确保低不可检测错误概率的一种有效方式。不过这种概率高度依赖于多项式的使用,将会带来选择合适多项式的困难,最终导致这安全要求较高的应用里面变得非常复杂,由于许多的数据可以在最小漏检概率下进行交换。
- 海明码 Hamming Code 是Error-correcting codes 纠错码的一种特别方式,纠错码可以确保数据发送通过一个由噪音的通信信道时无数据损坏。由发送者捆绑冗余信息到发送报文,因此即使原始数据在传输过程中有损坏,接受端也能完整恢复原始数据,比如手机静电干扰或大气干扰的传输错误。由于纠错码在传输即使部分受损的数据时也不需要进行重传,因此采用纠错码的海明码能有效增加通信的吞吐量。
- 海明码Hamming Code通过重复读取四位报文位,m1, m2, m3, m4,然后插入三位奇偶位,p1, p2, and p3,如果这7位其中 1 位在传输过程中受到损坏,接收端能检测到这个错误并且能完整恢复原始四位报文位。由于每一个数据单元中至多有 1 位能被纠错,因此这种方法叫做single-bit error correction。同时使用这种方法需要增加约75%的带宽,由于需要增加额外的3位奇偶位插入到四位报文中。
Reference
https://en.wikipedia.org/wiki/Parity_bit
https://en.wikipedia.org/wiki/Hamming_code
Cyclic Redundancy Check https://erg.abdn.ac.uk/users/gorry/course/dl-pages/crc.html