TensorFlow-Keras 18. DeepFM原理与自定义实现

一.引言

之前的文章中循序渐进的介绍过 LR，FM，WideAndDeep，有了这些模型的了解，接一下介绍当下比较流行的深度模型 DeepFm，WideAndDeep 结合了LR + DNN，DeepFM 结合了 FM + DNN，使得模型具备学习特征一阶，二阶以及高阶交叉的能力。

 

二.常见推荐系统

介绍DeepFM前，先看一下 LR，FM，DNN, WideAndDeep 以及 FM的演进过程:

1.LR

LR 是最早的线性模型，具备较强的记忆性，模型训练比较简单，因为只有一阶特征，所以有较好的解释性。

 

2.FM

LR 一阶特征不能对交叉特征有较好的表征，FM 解决了这个问题，通过为每个特征训练隐向量，两个特征交叉的权重可以由隐向量内积得到，从而解决了特征二阶交叉的问题。

 

3.DNN

LR 解决了一阶特征，FM 解决了二阶交叉特征，DNN 则解决了特征的高阶特征，随着层深度的增加，特征的交叉阶数不断地上升，模型有了更好的表征能力。

 

4.WideAndDeep

WideAndDeep 结合了 LR 的记忆能力又综合了 DNN 的高阶特征组合，获得更加平滑的结果。

 

5.DeepFM

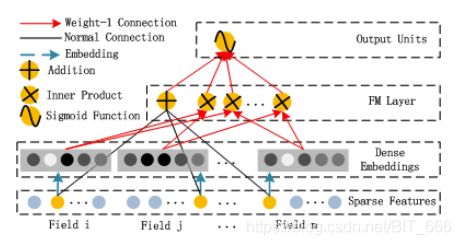
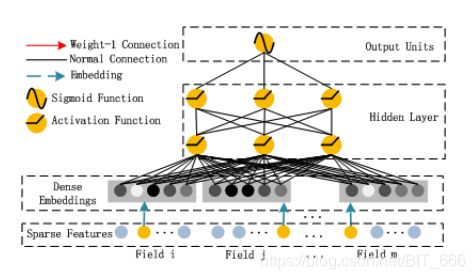
既然 WideAndDeep 引入了一阶特征和高阶特征，那么也可以引入二阶特征，这就是 DeepFM。DeepFM 目的是同时学习低阶和高阶的特征交叉，弥补了 WideAndDeep 的表征能力不足，主要由 FM 与 DNN 两部分构成，二者共用同一份输入共同训练，输入模型可以看作 :

                                                 

 

除了上述模型外，还有很多 FM，DeepFM 模型的衍生，例如 FFM，NFM，AFM，DIN，DIEN，DRN 等等，后续有时间可以研究~ 

 

三.DeepFM 自定义实现

上一篇文章已经对 FM 的具体公式，流程进行了详细分析，FM 侧相关问题可以参考 FM 自定义实现，下面基于 FM 层，在层内新增 DNN 单元，使得 Layer 可以同时训练 FM + DNN。

Tip:

导入类如下:

from tensorflow.keras import backend as K
from tensorflow.keras import layers, Model, optimizers, regularizers, losses
from tensorflow.keras.layers import Layer, Lambda, Dense, Input, Activation
import tensorflow as tf
import numpy as np

 

1.数据准备

    # 原始特征输入
    num_samples = 60000
    categoryA = np.random.randint(0, 100, (num_samples, 1))
    categoryB = np.random.randint(100, 200, (num_samples, 1))
    categoryC = np.random.randint(200, 300, (num_samples, 1))
    categoryD = np.random.randint(300, 400, (num_samples, 1))

    train = np.concatenate([categoryA, categoryB, categoryC, categoryD], axis=-1).astype('int32')
    print("训练数据样例与Size:")
    print(train[0:5])
    print(train.shape)

    labels = np.random.randint(0, 2, size=num_samples)
    labels = np.asarray(labels)
    print("样本labels:")
    print(labels[0:10])

num_samples 为训练样本数量，train 为训练数据，维度为 (None x 4)，labels 为标签，取值为0/1，数据均为 random 随机构造。 

训练数据样例与Size:
[[ 70 194 202 309]
 [ 19 195 241 324]
 [ 27 161 237 380]
 [  6 196 237 374]
 [ 43 191 219 316]]
(60000, 4)
样本labels:
[0 1 1 0 0 0 1 0 1 1]

 

2.DeepFM 层构建

DeepFM 层是 FM层 + DNN层，最后将二者的结果结合在一起 sigmoid 得到最终结果，所以 DeepFM层中需要单独实现 FM 与 DNN。这里按照 FM + 双隐层DNN 构造 DeemFm 模型。

(1) 输入参数含义 

feature_num : 特征数

output_dim : 隐向量输出维度

dense1_dim : 第一个隐层的维度

dense2_dim : 第二个隐层的维度

kernel_regularize : 正则化参数

activation : 激活函数 

 

(2) 层内函数功能 

init : 根据传参初始化相关参数，其中 dense1_dim，dense2_dim 默认 128 维度。

build : 构建 FM 参数矩阵，构造两个 Dense 层的 kernel 与 偏置 bias

call : 将 FM + DNN 得到的结果 concat ，送给最后的 sigmoid 处理

compute_output_shape : 计算输出样本维度，供 keras 自动推断

Tips : 这里需要注意的就是各个 weights 的维度，其他的逻辑都比较清晰，FM 层实现逻辑与前文一致，Dense 层实现逻辑为 activation(self.kernel * Tensor + self.bias)，其中 activation 选择为 relu。

relu = Lambda(lambda x: K.relu(x))

class DeepFM(Layer):
    """
        init: 初始化参数
        build: 定义权重
        call: 层的功能与逻辑
        compute_output_shape: 推断输出模型维度

    """

    def __init__(self, feat_num, out_dim, dense1_dim=128, dense2_dim=128, **kwargs):
        self.feature_num = feat_num
        self.output_dim = out_dim
        self.dense1_dim = dense1_dim
        self.dense2_dim = dense2_dim
        self.kernel_regularize = regularizers.l2(0.1)
        self.activation = Activation(relu)

        super().__init__(**kwargs)

    # 定义模型初始化 根据特征数目
    def build(self, input_shape):
        # 特征隐向量矩阵
        self.kernel = self.add_weight(name='kernel',
                                      shape=(self.feature_num, self.output_dim + 1),
                                      initializer='glorot_normal',
                                      regularizer=self.kernel_regularize,
                                      trainable=True)

        # DNN Dense1
        self.dense1 = self.add_weight(name='dense1',
                                      shape=(input_shape[1] * self.output_dim, self.dense1_dim),
                                      initializer='glorot_normal',
                                      trainable=True)

        # DNN Bias1
        self.bias1 = self.add_weight(name='bias1',
                                     shape=(self.dense1_dim, ),
                                     initializer='glorot_normal',
                                     trainable=True)

        # DNN Dense2
        self.dense2 = self.add_weight(name='dense2',
                                      shape=(self.dense1_dim, self.dense2_dim),
                                      initializer='glorot_normal',
                                      trainable=True)

        # DNN Bias1
        self.bias2 = self.add_weight(name='bias2',
                                     shape=(self.dense2_dim, ),
                                     initializer='glorot_normal',
                                     trainable=True)


        super(DeepFM, self).build(input_shape)  # Be sure to call this at the end

    def call(self, inputs, **kwargs):
        # input 为多个样本的稀疏特征表示

        # LR
        first_order = get_first_order(inputs, self.kernel)

        # FM
        seconder_order = get_second_order(inputs, self.kernel)

        # DNN
        deep_order = get_deep_order(inputs, self.kernel)
        activation_1 = self.activation(tf.matmul(deep_order, self.dense1) + self.bias1)
        activation_2 = self.activation(tf.matmul(activation_1, self.dense2) + self.bias2)

        # Concat
        concat_order = tf.concat([first_order, seconder_order, activation_2], axis=-1)
        return concat_order

    def compute_output_shape(self, input_shape):
        return input_shape(0)

 

(3) FM 部分

这里结合使用了 tf.nn 以及 keras.backend 的 Api，FM 公式与简化结果如下 :

         

# LR线性部分
def get_first_order(feat_index, args):
    embedding = tf.nn.embedding_lookup(args, feat_index)[:, :, -1]
    linear = K.sum(embedding, axis=-1)
    sum_embedding = K.expand_dims(linear, axis=1)
    return sum_embedding


# FM二阶交叉部分
def get_second_order(feat_index, args):
    embedding = tf.nn.embedding_lookup(args, feat_index)[:, :, :args.shape[-1] - 1]
    # 先求和再平方
    sum_embedding = K.sum(embedding, axis=1)
    sum_square = K.square(sum_embedding)
    # 先平方在求和
    squared = K.square(embedding)
    square_sum = K.sum(squared, axis=1)
    # 二阶交叉项
    second_order = 0.5 * tf.subtract(sum_square, square_sum)
    return second_order

 

(4) DNN 部分

外部 DNN 模块只 lookup 了对应特征的 Embedding 并 Flatten，Dense 层的逻辑在 call 函数内实现，因为需要在层内初始化 Dense 的权重，这里 Dense 层没有直接调用 layers 选择自己实现，效果大同小异。

# DNN高阶交叉部分
def get_deep_order(feat_index, args):
    # FM Args Shape: Feature_num * (K + 1)
    # Embedding Shape: Samples_num * Feature_num * K
    embedding = tf.nn.embedding_lookup(args, feat_index)[:, :, :args.shape[-1] - 1]
    # Flatten Shape: Samples_num * (Feature_num * K)
    embedding_flatten = layers.Flatten()(embedding)
    return embedding_flatten

# DNN
deep_order = get_deep_order(inputs, self.kernel)
activation_1 = self.activation(tf.matmul(deep_order, self.dense1) + self.bias1)
activation_2 = self.activation(tf.matmul(activation_1, self.dense2) + self.bias2)

 

3.DeepFM 模型编译

这里选择与上文 FM 相同的 feature_num 与 output_dim，由于是 CTR 问题，loss 依旧选择交叉熵，优化器可以自定义学习率等参数，其他参数也可自定义。

    # 构建模型
    feature_num = 400
    output_dim = 8
    deep_input = Input(shape=4, name='input', dtype='int32')
    deepFm_layer = DeepFM(feature_num, output_dim, name='DeepFM')(deep_input)
    result = Dense(1, activation='sigmoid', name='sigmoid')(deepFm_layer)
    deepFm_model = Model(deep_input, result)

    # 模型编译
    deepFm_model.compile(optimizer=optimizers.RMSprop(learning_rate=0.01),
                         loss=losses.binary_crossentropy,
                         metrics='accuracy')
    deepFm_model.summary()

 

4.模型训练与预测

epoch=10，batch_size=128训练模型，样本量为 60000。

    # 模型训练
    deepFm_model.fit(train, labels, epochs=10, batch_size=128)

    # 模型预测
    print("模型预测结果:")
    test_sample = [[1, 101, 201, 301], [7, 110, 222, 323], [81, 114, 270, 342], [63, 139, 204, 323],
                   [33, 173, 201, 396]]
    print(deepFm_model.predict(test_sample))

 由于样本随机，训练结果近似于随机预测。

 

5.隐向量权重获取

通过 layerName 获取对应 DeepFM 层，再根据索引获取对应权重即可，如果想获取 Dense 层和 Bias 权重，修改索引即可。

    # 获取线性权重与隐向量
    index = 100
    weights = deepFm_model.get_layer(name='DeepFM').get_weights()[0]
    vector = weights[index]
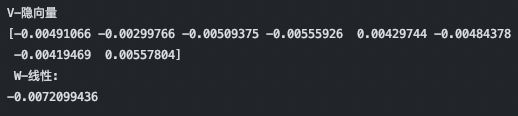
    print("V-隐向量")
    v = vector[:8]
    print(v)
    print(" W-线性:")
    w = vector[-1]
    print(w)

 

6.不同隐向量维度，Dense层维度，正则化系数对模型的影响

(1) 去掉FM层 L2 正则化参数 

去掉正则化参数模型的精度会提升，但是也会有过拟合。

 

(2) 增加隐向量维度 

增加隐向量维度，不修改 FM 正则化系数，模型效果变化不大。

 

(3) 增加 Dense 层维度 

Dense1_dim 和 Dense2_dim 扩大，不修改 FM 正则化系数，模型效果变化不大。

 

四.总结

有上一节 FM 的铺垫，这里在 FM 的基础上添加 DNN 并不困难，keras Api 的实现比较友好，但是有 bug 不好定位所以有利有弊，有问题欢迎交流~