Python实现一元及多元线性回归
Python实现线性回归
- 实现目标
- 实验数据
- 结果分析
-
- 数据集1下的回归分析
- 数据集2下的回归分析
- 源代码
实现目标
1.实现一元(或多元)线性回归
a. 根据对客观现象的定性认识初步判断现象之间的相关性
b. 绘制散点图
c. 进行回归分析,拟合出回归模型
d. 对回归模型进行检验—计算相关系数、异方差检验(散点图)
e. 进行回归预测
2实现离差形式的一元线性回归
实验数据
数据如下图,该数据为通过中国气象局数据库统计而来的2019年厦门市日平均气温数据(Data为1时日期为1月1日),该数据的散点图与折线图分别如图1图2所示。从图中可以看出厦门为典型的北半球夏季高温冬季低温气候,且存在波动。
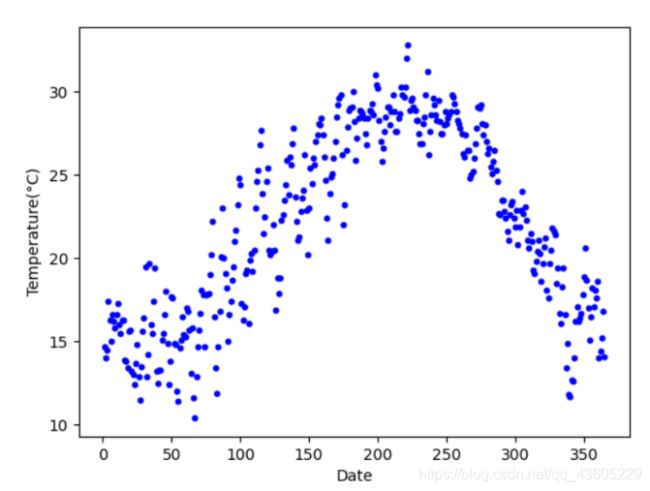
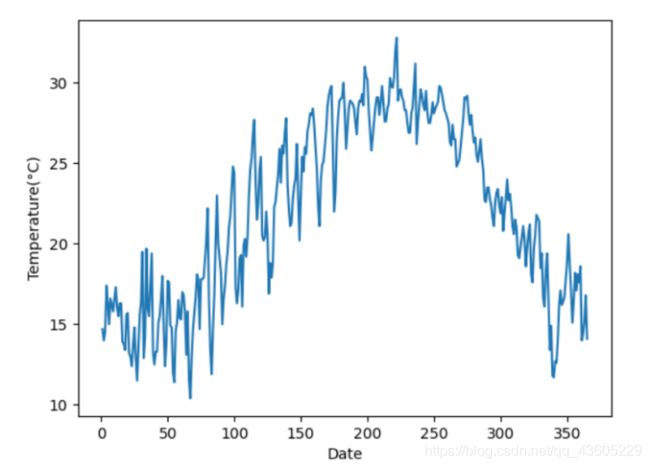
此外,为了方便进行一次线性回归及其相关操作,我取出一半数据(Data值为0至180)的数据进行线性回归模型的构建,如图3
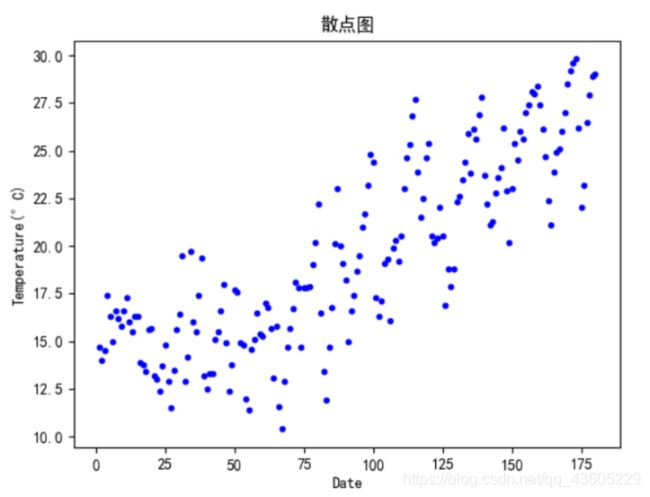
结果分析
数据集1下的回归分析

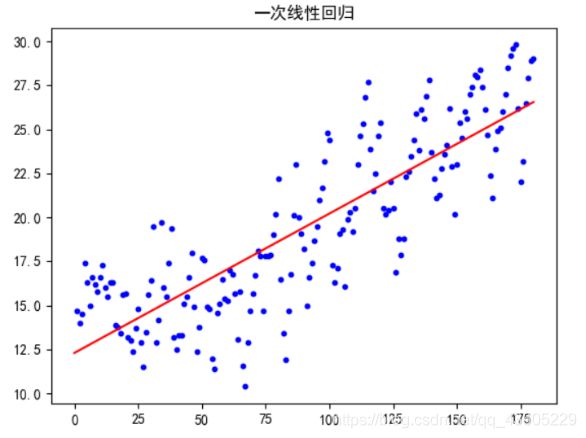
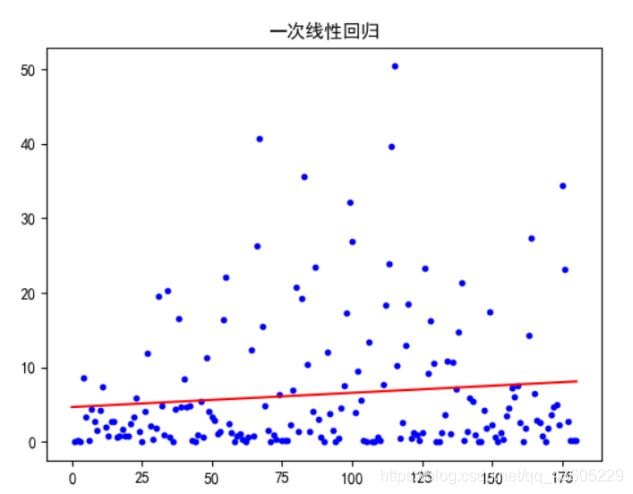
最终实验结果如图4所示,其中第一行表示一次回归模型的拟合函数,如图5所示,很明显的可以看出误差极大,因此我们对其进行二次回归
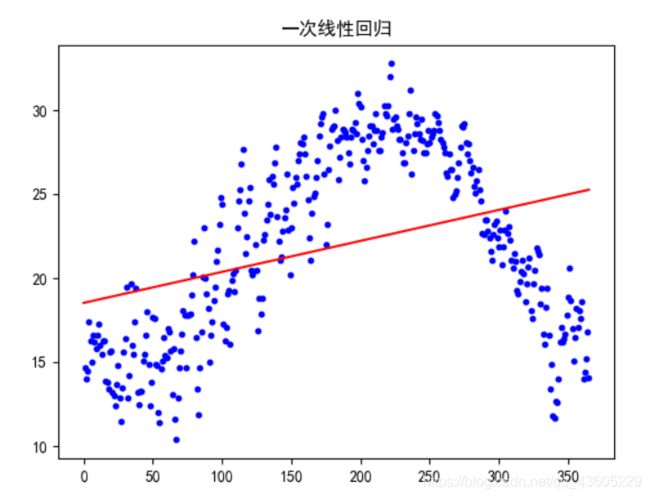
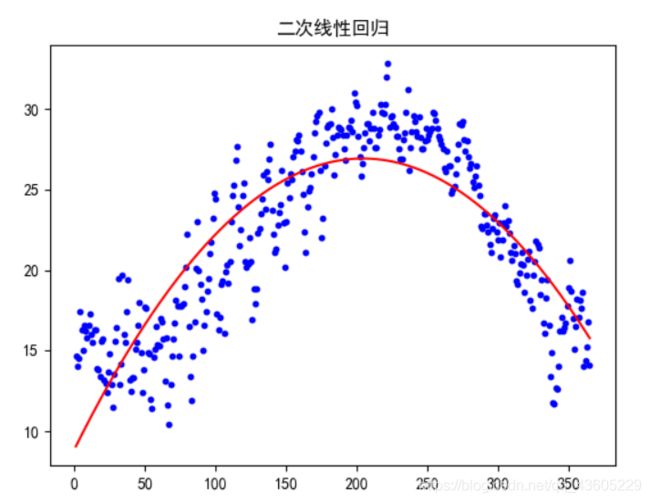
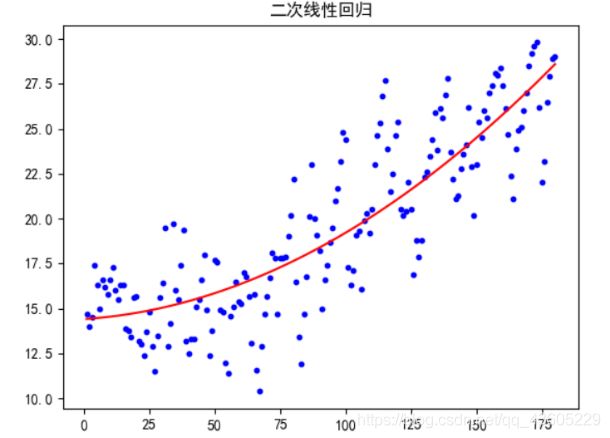
第二行结果为为此回归拟合函数,如图6所示,可以看出拟合效果较好
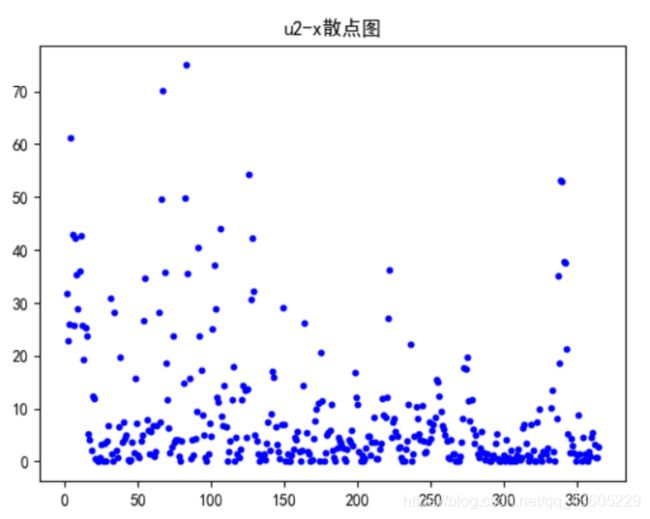
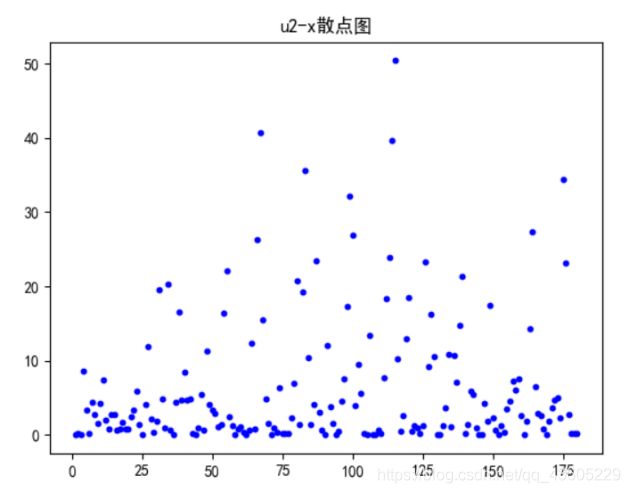
同时对一次线性回归计算得出相关系数为0.7861736064961535,u2-x散点图即其回归如图所示

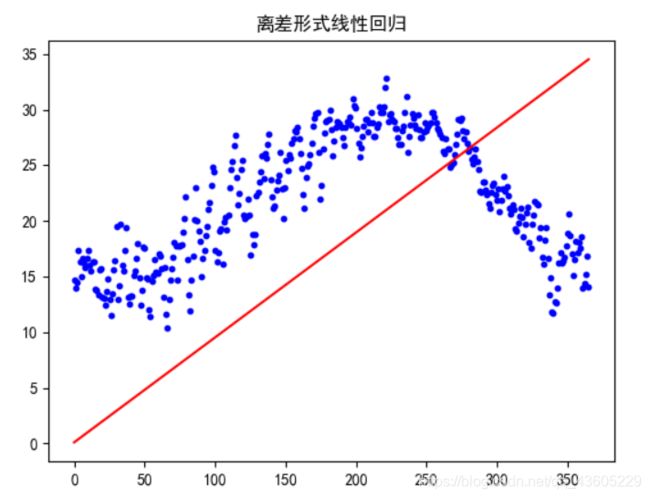
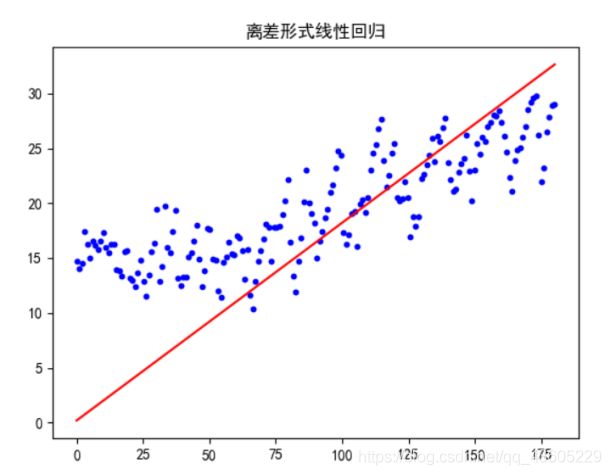
通过离差形式的线性回归拟合模型如下
数据集2下的回归分析

最终实验结果如图10所示,其余结果(图11-图15)解释同3.1.1
源代码
数据下载点这里:(data1)(data2)
import xlrd
from pylab import *
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
mpl.rcParams['font.sans-serif'] = ['SimHei']
def readFire(dataFir):
dataN=[]
dataX=[]
dataY=[]
table = dataFir.sheet_by_index(0)
for i in range(1,table.nrows):
line=table.row_values(i)
dataN.append(line)
dataN=np.array(dataN)
dataX = dataN[:,0]
dataY = dataN[:,4]
return dataX,dataY
def Visual(x, y):
plt.title('折线图')
plt.plot(x, y)
plt.xlabel("Date")
plt.ylabel("Temperature(°C)")
plt.show()
plt.title('散点图')
plt.scatter(x, y,s=10,color="b")
plt.xlabel("Date")
plt.ylabel("Temperature(°C)")
plt.show()
def Regression1(x,y):
n=len(x)
xx=0
xy=0
xAvg=0
yAvg=0
for i in range(n):
xy = xy + x[i]*y[i]
xx = xx + x[i]*x[i]
xAvg = xAvg + x[i]
yAvg = yAvg + y[i]
xAvg=xAvg/n
yAvg=yAvg/n
b = (xy-n*xAvg*yAvg)/(xx-n*xAvg*xAvg)
a = yAvg - b*xAvg
print('一次回归方程为:y=',b,'* x +',a)
plt.title('一次线性回归')
plt.scatter(x,y,s=10,color="b")
x=np.linspace(0,n,n)
yp=b*x+a
plt.plot(x,yp,color="r")
plt.show()
def Regression2(x, y):
X = x.reshape(-1,1)
X2 = np.hstack([X**2,X])
lr = LinearRegression()
lr.fit(X2,y)
print('二次回归方程为:y=',lr.coef_[0],'x^2 *',
lr.coef_[1],'x +',lr.intercept_)
yp = lr.predict(X2)
plt.title('二次线性回归')
plt.scatter(x,y,s=10,color="b")
plt.plot(x,yp,color='r')
plt.show()
XGXS(x,y,yp)
def XGXS(x,y,yp):
n=len(x)
y1=0
y2=0
yAvg=0
for i in range(n):
yAvg = yAvg + y[i]
yA=yAvg/n
for i in range(n):
y1 = y1+(yp[i]-yA)**2
y2 = y2+(y[i]-yA)**2
u2 = (y-yp)**2
plt.title('u2-x散点图')
plt.scatter(x,u2,s=10,color="b")
plt.show()
print('回归模型检验:')
R=pow(y1/y2,.5)
print('相关系数为:',R)
Regression1(x,u2)
def LiCha(x,y):
n=len(x)
xMat = np.mat(x).T
yMat = np.mat(y)
xTx = xMat.T * xMat
ws = xTx.I * xMat.T * yMat.T
x=np.linspace(0,n,n)
yp = xMat * ws
print('离差回归方程为:y=',ws,'* x ')
plt.title('离差形式线性回归')
plt.scatter(x,y,s=10,color="b")
plt.plot(x,yp,color="r")
plt.show()
if __name__ == '__main__':
dataFir = xlrd.open_workbook("data2.xlsx")
dataX,dataY = readFire(dataFir)
#可视化数据
Visual(dataX, dataY)
#一次线性回归
Regression1(dataX,dataY)
#二次线性回归
Regression2(dataX, dataY)
#离差形式线性回归
LiCha(dataX,dataY)