神经网络的数学基础
神经网络的数学基础
-
- 2.1初识神经网络
- 2.2 神经网络的数据表示
-
- 2.2.1 标量(0D张量)
- 2.2.2 向量(1D张量)
- 2.2.3 矩阵(2D张量)
- 2.2.4 3D张量与更高维张量
- 2.2.5 关键属性
- 2.2.6 在Numpy中操作张量
- 2.2.7 数据批量的概念
- 2.2.8 现实世界中的数据张量
- 2.2.9 向量数据
- 2.2.10时间序列数据或序列数据
- 2.2.11 图像数据
- 2.2.12 视频数据
- 2.3 张量运算
-
- 2.3.1 逐元素运算
- 2.3.2 广播(Broadcast)
- 2.3.3 张量点积
- 2.3.4 张量变形
- 2.4 神经网络的“引擎”:基于梯度的优化
-
- 2.4.1 随机梯度下降
- 2.4.2 链式求导:反向传播算法
2.1初识神经网络
- 我们这里要解决的问题是,将手写数字的灰度图像(28 像素×28 像素)划分到 10 个类别中(0~9)。
- 在机器学习中,分类问题中的某个类别叫作类(class)。数据点叫作样本(sample)。某个样本对应的类叫作标签(label)。
- 加载数据
from keras.datasets import mnist (train_images, train_labels), (test_images, test_labels) = mnist.load_data()
- train_images 和 train_labels 组成了训练集(training set),模型将从这些数据中进行学习。然后在测试集(test set,即 test_images 和 test_labels)上对模型进行测试。图像被编码为 Numpy 数组,而标签是数字数组,取值范围为 0~9。图像和标签一一对应。
- 接下来的工作流程如下:首先,将训练数据(train_images 和 train_labels)输入神经网络;其次,网络学习将图像和标签关联在一起;最后,网络对 test_images 生成预测,而我们将验证这些预测与 test_labels 中的标签是否匹配。
- 搭建网络
from keras import models from keras import layers network = models.Sequential() network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,))) network.add(layers.Dense(10, activation='softmax'))
- 神经网络的核心组件是层(layer),它是一种数据处理模块,你可以将它看成数据过滤器。进去一些数据,出来的数据变得更加有用。
- 本例中的网络包含 2 个 Dense 层,它们是密集连接(也叫全连接)的神经层。第二层(也是最后一层)是一个 10 路 softmax 层,它将返回一个由 10 个概率值(总和为 1)组成的数组。每个概率值表示当前数字图像属于 10 个数字类别中某一个的概率。
- 编译
network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
- 要想训练网络,我们还需要选择编译(compile)步骤的三个参数。
- 损失函数(loss function):网络如何衡量在训练数据上的性能,即网络如何朝着正确的方向前进。
- 优化器(optimizer):基于训练数据和损失函数来更新网络的机制。
- 在训练和测试过程中需要监控的指标(metric):本例只关心精度,即正确分类的图像所占的比例。
- 准备图像数据
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
- 在开始训练之前,我们将对数据进行预处理,将其变换为网络要求的形状,并缩放到所有值都在 [0, 1] 区间。比如,之前训练图像保存在一个 uint8 类型的数组中,其形状为(60000, 28, 28),取值区间为 [0, 255]。我们需要将其变换为一个 float32 数组,其形状为 (60000, 28 * 28),取值范围为 0~1。
- 准备标签
from keras.utils import to_categorical
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
- 训练
>>> network.fit(train_images, train_labels, epochs=5, batch_size=128)
Epoch 1/5
60000/60000 [=============================] - 9s - loss: 0.2524 - acc: 0.9273
Epoch 2/5
51328/60000 [=======================>.....] - ETA: 1s - loss: 0.1035 - acc: 0.9692
- 训练过程中显示了两个数字:一个是网络在训练数据上的损失(loss),另一个是网络在训练数据上的精度(acc)。
我们很快就在训练数据上达到了 0.989(98.9%)的精度。现在我们来检查一下模型在测试集上的性能。
>>> test_loss, test_acc = network.evaluate(test_images, test_labels)
>>> print('test_acc:', test_acc)
test_acc: 0.9785
- 测试集精度为 97.8%,比训练集精度低不少。训练精度和测试精度之间的这种差距是过拟合(overfit)造成的。过拟合是指机器学习模型在新数据上的性能往往比在训练数据上要差。
2.2 神经网络的数据表示
- 前面例子使用的数据存储在多维 Numpy 数组中,也叫张量(tensor)。
- 张量这一概念的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。你可能对矩阵很熟悉,它是二维张量。张量是矩阵向任意维度的推广[注意,张量的维度(dimension)通常叫作轴(axis)]
2.2.1 标量(0D张量)
- 仅包含一个数字的张量叫作标量(scalar,也叫标量张量、零维张量、0D 张量)。在 Numpy中,一个 float32 或 float64 的数字就是一个标量张量(或标量数组)。
>>> import numpy as np
>>> x = np.array(12)
>>> x
array(12)
>>> x.ndim
0
2.2.2 向量(1D张量)
- 数字组成的数组叫作向量(vector)或一维张量(1D 张量)。一维张量只有一个轴。下面是一个 Numpy 向量。
>>> x = np.array([12, 3, 6, 14, 7])
>>> x
array([12, 3, 6, 14, 7])
>>> x.ndim
1
- 这个向量有 5 个元素,所以被称为 5D 向量。不要把 5D 向量和 5D 张量弄混! 5D 向量只有一个轴,沿着轴有 5 个维度,而 5D 张量有 5 个轴(沿着每个轴可能有任意个维度)。维度(dimensionality)可以表示沿着某个轴上的元素个数(比如 5D 向量),也可以表示张量中轴的个数(比如 5D 张量),这有时会令人感到混乱。对于后一种情况,技术上更准确的说法是 5 阶张量(张量的阶数即轴的个数),但 5D 张量这种模糊的写法更常见。
2.2.3 矩阵(2D张量)
向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量)。矩阵有 2 个轴(通常叫作行和列)。你可以将矩阵直观地理解为数字组成的矩形网格。下面是一个 Numpy 矩阵。
>>> x = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
>>> x.ndim
2
- 第一个轴上的元素叫作行(row),第二个轴上的元素叫作(column)。在上面的例子中,[5, 78, 2, 34, 0] 是 x 的第一行,[5, 6, 7] 是第一列。
2.2.4 3D张量与更高维张量
- 将多个矩阵组合成一个新的数组,可以得到一个 3D 张量,你可以将其直观地理解为数字组成的立方体。下面是一个 Numpy 的 3D 张量。
>>> x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
>>> x.ndim
3
- 将多个 3D 张量组合成一个数组,可以创建一个 4D 张量,以此类推。深度学习处理的一般是 0D 到 4D 的张量,但处理视频数据时可能会遇到 5D 张量。
2.2.5 关键属性
张量是由以下三个关键属性来定义的。
- 轴的个数(阶) 例如,3D 张量有 3 个轴,矩阵有 2 个轴。这在 Numpy 等 Python 库中也叫张量的 ndim。
- 形状。这是一个整数元组,表示张量沿每个轴的维度大小(元素个数)。例如,前面矩阵示例的形状为 (3, 5),3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个元素,比如 (5,),而标量的形状为空,即 ()。
- 数据类型(在 Python 库中通常叫作 dtype)。这是张量中所包含数据的类型,例如,张量的类型可以是 float32、uint8、float64 等。在极少数情况下,你可能会遇到字符(char)张量。注意,Numpy(以及大多数其他库)中不存在字符串张量,因为张量存储在预先分配的连续内存段中,而字符串的长度是可变的,无法用这种方式存储。
2.2.6 在Numpy中操作张量
- 例1
digit = train_images[4]
import matplotlib.pyplot as plt
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()
- 在这个例子中,我们使用语法 train_images[i] 来选择沿着第一个轴的特定数字。选择张量的特定元素叫作张量切片(tensor slicing)。我们来看一下 Numpy 数组上的张量切片运算。
- 例2
- 下面这个例子选择第 10~100 个数字(不包括第 100 个),并将其放在形状为 (90, 28, 28) 的数组中。
>>> my_slice = train_images[10:100]
>>> print(my_slice.shape)
(90, 28, 28)
它等同于下面这个更复杂的写法,给出了切片沿着每个张量轴的起始索引和结束索引。注意,: 等同于选择整个轴。
>>> my_slice = train_images[10:100, :, :]
>>> my_slice.shape
(90, 28, 28)
>>> my_slice = train_images[10:100, 0:28, 0:28]
>>> my_slice.shape
(90, 28, 28)
- 例3
- 一般来说,你可以沿着每个张量轴在任意两个索引之间进行选择。例如,你可以在所有图像的右下角选出 14 像素×14 像素的区域:
my_slice = train_images[:, 14:, 14:]
- 也可以使用负数索引。与 Python 列表中的负数索引类似,它表示与当前轴终点的相对位置。你可以在图像中心裁剪出 14 像素×14 像素的区域:
my_slice = train_images[:, 7:-7, 7:-7]
2.2.7 数据批量的概念
- 通常来说,深度学习中所有数据张量的第一个轴(0 轴,因为索引从 0 开始)都是样本轴(samples axis,有时也叫样本维度)。此外,深度学习模型不会同时处理整个数据集,而是将数据拆分成小批量。具体来看,下面是 MNIST 数据集的一个批量,批量大小为 128:
- batch = train_images[:128]
然后是下一个批量。
batch = train_images[128:256]
然后是第 n 个批量。
batch = train_images[128 * n:128 * (n + 1)] - 对于这种批量张量,第一个轴(0 轴)叫作批量轴(batch axis)或批量维度(batch dimension)。在使用 Keras 和其他深度学习库时,你会经常遇到这个术语。
2.2.8 现实世界中的数据张量
- 向量数据:2D 张量,形状为 (samples, features)。
- 时间序列数据或序列数据:3D 张量,形状为 (samples, timesteps, features)。
- 图像:4D 张量,形状为 (samples, height, width, channels) 或 (samples, channels, height, width)。
- 视频:5D 张量,形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)。
2.2.9 向量数据
- 这是最常见的数据。对于这种数据集,每个数据点都被编码为一个向量,因此一个数据批量就被编码为 2D 张量(即向量组成的数组),其中第一个轴是样本轴,第二个轴是特征轴。
- 例子:
- 人口统计数据集,其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量,而整个数据集包含 100 000 个人,因此可以存储在形状为 (100000, 3) 的 2D张量中。
- 文本文档数据集,我们将每个文档表示为每个单词在其中出现的次数(字典中包含20 000 个常见单词)。每个文档可以被编码为包含 20 000 个值的向量(每个值对应于字典中每个单词的出现次数),整个数据集包含 500 个文档,因此可以存储在形状为(500, 20000) 的张量中。
2.2.10时间序列数据或序列数据
当时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的 3D 张量中。每个样本可以被编码为一个向量序列(即 2D 张量),因此一个数据批量就被编码为一个 3D 张量。
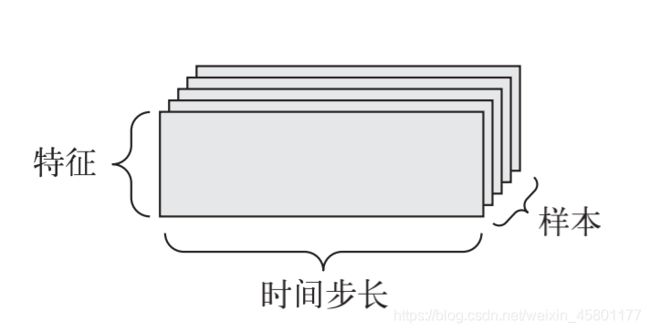
根据惯例,时间轴始终是第 2 个轴(索引为 1 的轴)。
- 例子:
- 股票价格数据集。每一分钟,我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个 3D 向量,整个交易日被编码为一个形状为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),而 250 天的数据则可以保存在一个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
- 推文数据集。我们将每条推文编码为 280 个字符组成的序列,而每个字符又来自于 128个字符组成的字母表。在这种情况下,每个字符可以被编码为大小为 128 的二进制向量(只有在该字符对应的索引位置取值为 1,其他元素都为 0)。那么每条推文可以被编码为一个形状为 (280, 128) 的 2D 张量,而包含 100 万条推文的数据集则可以存储在一个形状为 (1000000, 280, 128) 的张量中。
2.2.11 图像数据
图像通常具有三个维度:高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道,因此可以保存在 2D 张量中,但按照惯例,图像张量始终都是 3D 张量,灰度图像的彩色通道只有一维。因此,如果图像大小为256×256,那么 128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中,而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中。
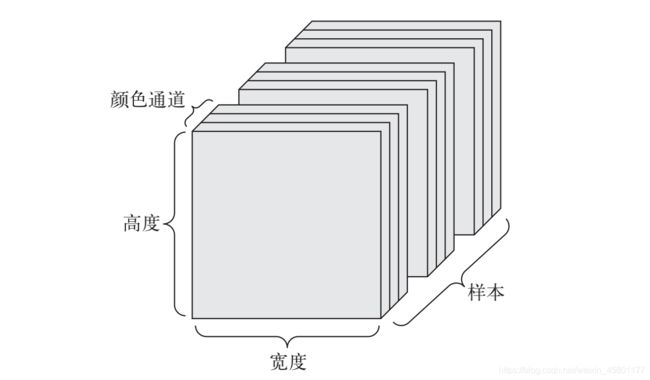
- 图像张量的形状有两种约定:通道在后(channels-last)的约定(在 TensorFlow 中使用)和通道在前(channels-first)的约定(在 Theano 中使用)。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后:(samples, height, width, color_depth)。与此相反,Theano将图像深度轴放在批量轴之后:(samples, color_depth, height, width)。如果采
用 Theano 约定,前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。Keras 框架同时支持这两种格式。
2.2.12 视频数据
- 视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧,每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中,而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为(samples, frames, height, width, color_depth)。举个例子,一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144×256,这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。总共有 106 168 320 个值!如果张量的数据类型(dtype)是float32,每个值都是32 位,那么这个张量共有 405MB。好大!你在现实生活中遇到的视频要小得多,因为它们不以float32 格式存储,而且通常被大大压缩,比如 MPEG 格式。
2.3 张量运算
深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算(tensor operation)例如加上张量、乘以张量等。
在最开始的例子中,我们通过叠加 Dense 层来构建网络。Keras 层的实例如下所示。
keras.layers.Dense(512, activation='relu')
这个层可以理解为一个函数,输入一个 2D 张量,返回另一个 2D 张量,即输入张量的新表示。具体而言,这个函数如下所示(其中 W 是一个 2D 张量,b 是一个向量,二者都是该层的属性)。
output = relu(dot(W, input) + b)
我们将上式拆开来看。这里有三个张量运算:输入张量和张量 W 之间的点积运算(dot)、得到的 2D 张量与向量 b 之间的加法运算(+)、最后的 relu 运算。relu(x) 是 max(x, 0)。
2.3.1 逐元素运算
relu 运算和加法都是逐元素(element-wise)的运算,即该运算独立地应用于张量中的每个元素。
- 我们可以用for循环实现逐元素运算:
def naive_relu(x):
assert len(x.shape) == 2
#确认x是一个Numpy的2D张量,防止出错
x = x.copy()
#避免覆盖张量
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] = max(x[i, j], 0)
return x
def naive_add(x, y):
assert len(x.shape) == 2
assert x.shape == y.shape
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += y[i, j]
return x
- 我们也可以使用Numpy内置的函数直接进行计算:
import numpy as np
z = x + y
z = np.maximum(z, 0.)
2.3.2 广播(Broadcast)
- 较小的张量会被广播(broadcast),以匹配较大张量的形状。广播包含以下两步。
- 向较小的张量添加轴(叫作广播轴),使其ndim 与较大的张量相同。
- 将较小的张量沿着新轴重复,使其形状与较大的张量相同。
- 例子:假设 X 的形状是 (32, 10),y 的形状是 (10,)。首先,我们给 y添加空的第一个轴,这样 y 的形状变为 (1, 10)。然后,我们将 y 沿着新轴重复 32 次,这样得到的张量 Y 的形状为 (32, 10),并且
Y[i, :] == y for i in range(0, 32)。现在,我们可以将 X 和 Y 相加,因为它们的形状相同。
def naive_add_matrix_and_vector(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0]
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += y[j]
return x
-如果一个张量的形状是 (a, b, … n, n+1, …m),另一个张量的形状是 (n, n+1, … m),那么你通常可以利用广播对它们做两个张量之间的逐元素运算。广播操作会自动应用于从 a 到 n-1 的轴。下面这个例子利用广播将逐元素的 maximum 运算应用于两个形状不同的张量。
import numpy as np
x = np.random.random((64, 3, 32, 10))
y = np.random.random((32, 10))
z = np.maximum(x, y)#输出形状是(64, 3, 32, 10)与x相同
2.3.3 张量点积
- 点积运算,也叫张量积(tensor product,不要与逐元素的乘积弄混),是最常见也最有用的张量运算。与逐元素的运算不同,它将输入张量的元素合并在一起。在 Numpy、Keras、Theano 和 TensorFlow 中,都是用 * 实现逐元素乘积。TensorFlow 中的点积使用了不同的语法,但在 Numpy 和 Keras 中,都是用标准的 dot 运算符来实现点积。
import numpy as np
z = np.dot(x, y)
- 从数学的角度来看,点积运算做了什么?我们首先看一下两个向量 x 和 y 的点积。其计算过程如下。
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return z
-注意,两个向量之间的点积是一个标量,而且只有元素个数相同的向量之间才能做点积。
你还可以对一个矩阵 x 和一个向量 y 做点积,返回值是一个向量,其中每个元素是 y 和 x的每一行之间的点积。其实现过程如下。
import numpy as np
def naive_matrix_vector_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0]
z = np.zeros(x.shape[0])
for i in range(x.shape[0]):
for j in range(x.shape[1]):
z[i] += x[i, j] * y[j]
return z
- 注意,如果两个张量中有一个的 ndim 大于 1,那么 dot 运算就不再是对称的,也就是说,dot(x, y) 不等于 dot(y, x)。
- 当然,点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。对于两个矩阵 x 和 y,当且仅当 x.shape[1] == y.shape[0] 时,你才可以对它们做点积(dot(x, y))。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵,其元素为 x的行与 y 的列之间的点积。其简单实现如下。
def naive_matrix_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 2
assert x.shape[1] == y.shape[0]
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
for j in range(y.shape[1]):
row_x = x[i, :]
column_y = y[:, j]
z[i, j] = naive_vector_dot(row_x, column_y)
return z
- 更一般地说,你可以对更高维的张量做点积,只要其形状匹配遵循与前面 2D 张量相同的原则:
(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)
以此类推。
2.3.4 张量变形
- 张量变形是指改变张量的行和列,以得到想要的形状。变形后的张量的元素总个数与初始张量相同。简单的例子可以帮助我们理解张量变形。
>>> x = np.array([[0., 1.],
[2., 3.],
[4., 5.]])
>>> print(x.shape)
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]])
- 经常遇到的一种特殊的张量变形是转置(transposition)。对矩阵做转置是指将行和列互换,使 x[i, :] 变为 x[:, i]。
>>> x = np.zeros((300, 20))
>>> x = np.transpose(x)
>>> print(x.shape)
(20, 300)
2.4 神经网络的“引擎”:基于梯度的优化
output = relu(dot(W, input) + b)
- 在这个表达式中,W 和 b 都是张量,均为该层的属性。它们被称为该层的权重(weight)或可训练参数(trainable parameter),分别对应 kernel 和 bias 属性。这些权重包含网络从观察训练数据中学到的信息。
- 一开始,这些权重矩阵取较小的随机值,这一步叫作随机初始化(random initialization)。当然,W 和 b 都是随机的,relu(dot(W, input) + b) 肯定不会得到任何有用的表示。虽然得到的表示是没有意义的,但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这个逐渐调节的过程叫作训练,也就是机器学习中的学习。
- 上述过程发生在一个训练循环(training loop)内,其具体过程如下。必要时一直重复这些步骤。
- 抽取训练样本 x 和对应目标 y 组成的数据批量。
- 在 x 上运行网络[这一步叫作前向传播(forward pass)],得到预测值 y_pred。
- 计算网络在这批数据上的损失,用于衡量 y_pred 和 y 之间的距离。
- 更新网络的所有权重,使网络在这批数据上的损失略微下降。
- 最终得到的网络在训练数据上的损失非常小,即预测值 y_pred 和预期目标 y 之间的距离非常小。网络“学会”将输入映射到正确的目标。
2.4.1 随机梯度下降
-
给定一个可微函数,理论上可以用解析法找到它的最小值:函数的最小值是导数为 0 的点,因此你只需找到所有导数为 0 的点,然后计算函数在其中哪个点具有最小值。
-
将这一方法应用于神经网络,就是用解析法求出最小损失函数对应的所有权重值。可以通过对方程 gradient(f)(W) = 0 求解 W 来实现这一方法。这是包含 N 个变量的多项式方程,其中 N 是网络中系数的个数。N=2 或 N=3 时可以对这样的方程求解,但对于实际的神经网络是无法求解的,因为参数的个数不会少于几千个,而且经常有上千万个。
-
我们可以将上个部分的第四步改为
- 计算损失相对于网络参数的梯度[一次反向传播(backward pass)]。
- 将参数沿着梯度的反方向移动一点,比如 W -= step * gradient,从而使这批数据
上的损失减小一点。
-
注意,小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标,而不是抽取一批数据。这叫作真 SGD(有别于小批量 SGD)。还有另一种极端,每一次迭代都在所有数据上运行,这叫作批量 SGD。这样做的话,每次更新都更加准确,但计算代价也高得多。这两个极端之间的有效折中则是选择合理的批量大小。
-
此外,SGD 还有多种变体,其区别在于计算下一次权重更新时还要考虑上一次权重更新,而不是仅仅考虑当前梯度值,比如带动量的 SGD、Adagrad、RMSProp 等变体。这些变体被称为优化方法(optimization method)或优化器(optimizer)。其中动量的概念尤其值得关注,它在许多变体中都有应用。动量解决了 SGD 的两个问题:收敛速度和局部极小点。有一种有用的思维图像,就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大,那么它不会卡在峡谷里,最终会到达全局最小点。动量方法的实现过程是每一步都移动小球,不仅要考虑当前的斜率值(当前的加速度),还要考虑当前的速度(来自于之前的加速度)。这在实践中的是指,更新参数 w 不仅要考虑当前的梯度值,还要考虑上一次的参数更新,其简单实现如下所示。
past_velocity = 0.
momentum = 0.1 #不变的动量因子
while loss > 0.01: #优化的循环
w, loss, gradient = get_current_parameters()
velocity = past_velocity * momentum - learning_rate * gradient
w = w + momentum * velocity - learning_rate * gradient
past_velocity = velocity
update_parameter(w)
2.4.2 链式求导:反向传播算法
- 在实践中,神经网络函数包含许多连接在一起的张量运算,每个运算都有简单的、已知的导数。例如,下面这个网络 f 包含 3 个张量运算 a、b 和 c,还有 3 个权重矩阵 W1、W2 和 W3。
f(W1, W2, W3) = a(W1, b(W2, c(W3))) - 根据微积分的知识,这种函数链可以利用下面这个恒等式进行求导,它称为链式法则(chain rule):(f(g(x)))’ = f’(g(x)) * g’(x)。将链式法则应用于神经网络梯度值的计算,得到的算法叫作反向传播(backpropagation,有时也叫反式微分,reverse-mode differentiation)。反向传播从最终损失值开始,从最顶层反向作用至最底层,利用链式法则计算每个参数对损失值的贡献大小。
