假设有M个样本,m个特征,N个类别,即:
其中
令表示第个样本在第类上的真实得分值,则有:
令表示预测的第类样本在第类上的得分值。
则多分类的损失函数定义如下:
其中是交叉熵损失函数,是惩罚项。
如何求解?
现假设前棵树已经生成,为了表述方便,给出如下的几个符号定义:
| 符号 | 含义 |
|---|---|
| 第t个boost第个样本在第类上的得分 | |
| 前t-1个boost的累加得分 |
由此定义如下的损失函数:
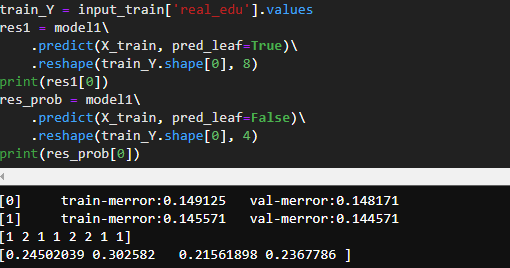
对于这个公式,我们给出一个简单的例子来验证。现在假设有树的最高深度是1,限定boost为2,我们打印样本在每个boost上的得分(即落在哪个叶子节点上)
"""
0:[edu4<159.587] yes=1,no=2,missing=1
1:leaf=-0.0608645
2:leaf=0.117652
booster[1]:
0:[edu1<378.454] yes=1,no=2,missing=1
1:leaf=-0.0617213
2:leaf=0.136535
booster[2]:
0:[edu2<166.643] yes=1,no=2,missing=1
1:leaf=-0.0428214
2:leaf=0.14372
booster[3]:
0:[edu3<99.8889] yes=1,no=2,missing=1
1:leaf=0.00749163
2:leaf=0.181717
booster[4]:
0:[edu4<157.801] yes=1,no=2,missing=1
1:leaf=-0.0594841
2:leaf=0.102977
booster[5]:
0:[edu1<363.302] yes=1,no=2,missing=1
1:leaf=-0.0603631
2:leaf=0.116588
booster[6]:
0:[edu2<160.402] yes=1,no=2,missing=1
1:leaf=-0.0428952
2:leaf=0.117361
booster[7]:
0:[edu3<99.3995] yes=1,no=2,missing=1
1:leaf=0.000404452
2:leaf=0.14999
'''
如上图所示,该样本分别落在了第1 2 1 1 2 2 1 1 个叶子节点上,对应的得分值为:
-0.0608645 0.136535 -0.0428214 0.00749163 0.102977 0.116588 -0.0428952 0.000404452。为了验证我们做如下的实验:(验证代码有点戳)
# 计算sofatmax后的值
def fun(array):
sum = 0
for i in range(0, len(array)):
sum = sum + np.e ** array[i]
res = []
for i in range(0, len(array)):
res.append((np.e ** array[i]) / sum)
return res
# 将所有叶子节点上的值放到一个数组中
arr2 = [[-0.0608645, 0.117652],
[-0.0617213, 0.136535],
[-0.0428214, 0.14372],
[0.00749163, 0.181717],
[-0.0594841, 0.102977],
[-0.0603631, 0.116588],
[-0.0428952, 0.117361],
[0.000404452, 0.14999]]
# 计算该样本所对应的得分值
round1_leaf_calue = []
for i in range(len(res1)):
round1_leaf_calue.append([
arr2[0][res1[i][0]-1],
arr2[1][res1[i][1]-1],
arr2[2][res1[i][2]-1],
arr2[3][res1[i][3]-1],
])
# 计算对应的概率值
print(fun(round1_leaf_calue ))
# [0.24502039 0.302582 0.21561898 0.2367786 ]
可见每类上的的得分值只与其同类别的的得分值有关系。
将损失函数在处泰勒展开(注意此处是向量函数的泰勒展开,第一次理解该问题的时候以后是标量的,然后就一直推导错误)
为了后续求解方便,假设惩罚项叶子节点的值的平方和。假设第个boost的n颗树(对应为第n+1个类别上的得分值)有个叶子节点,第个叶子节点上的样本结合表示为:
即第个样本落在第个boost的第类的树上的第个叶子节点上。故惩罚项定义为:
则损失函数二级泰勒近似后有:
显然损失函数是关于的二次的,由凸优化的理论知,最优点在一阶导数为零处取得,因此有:
因此只要求出和即可。
重写损失函数如下:
若记为个boost后第个样本在第类上的概率值, 则:
假设,即有。上述一阶二阶导即可简化为:
对比源码中的逻辑
在src/objective/multiclass_obj.cu脚本中
// Part of Softmax function
//源码中给出注释,实际上就是求一个softmax
bst_float wmax = std::numeric_limits::min();
for (auto const i : point) { wmax = fmaxf(i, wmax); }
double wsum = 0.0f;
for (auto const i : point) { wsum += expf(i - wmax); }
auto label = labels[idx];
if (label < 0 || label >= nclass) {
_label_correct[0] = 0;
label = 0;
}
bst_float wt = is_null_weight ? 1.0f : weights[idx];
for (int k = 0; k < nclass; ++k) {
// Computation duplicated to avoid creating a cache.
bst_float p = expf(point[k] - wmax) / static_cast(wsum);
const float eps = 1e-16f;
const bst_float h = fmax(2.0f * p * (1.0f - p) * wt, eps);
//当所求类别等于真实类别时为p-1否则为p,与所推相符
p = label == k ? p - 1.0f : p;
gpair[idx * nclass + k] = GradientPair(p * wt, h);
下一篇分享该部分的源码解读