打个广告,java技术交流群:130031711,欢迎大家踊跃加入!
最长上升子序列
题目:给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
思路:这个题有种似曾相识的感觉啊。但是我没明白题目的2 3 7 101。是指可以跳着?那2 5 7 101是不是也可以?再换个角度,是不是这样应该用dp来做?我反正直觉上觉得dp可以的。。。到第一位,最长串1,第二位最长串还是1,第三位,最长串1, 第四位最长串2。到第五串,最长串还是2.但是边界值变成了3,第六位变成了3.。。。我直觉是这样,具体怎么做还是要代码实现的,另外我记得之前一个类似的题目是有波线图,也不知道有没有用。我先去写代码试试了。
额,果然实现和想象有点不同,我随着做随着改思路,最终完全不是dp了。哈哈。先贴代码再说心路历程:
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length==0) return 0;
//这里用Integer如果不赋值是null
int[] d = new int[nums.length];
d[0] = Integer.MAX_VALUE;
int lastIdx = 0;
for(int i = 0;id[lastIdx]){
lastIdx++;
d[lastIdx] = n;
}else{
for(int j = 0;j<=lastIdx;j++){
if(d[j]==n) break;//这个元素已经出现了直接pass,不然可能出现相同元素都占位
if(d[j]>n){
d[j] = n;
break;
}
}
}
}
return lastIdx+1;
}
}
先说dp,dp是选和不选的问题,本来我的想法是两个比较点是前一个数的连续数和比当前数小的第一个数的个数+1。然后发现这里就需要遍历到比当前数小的第一个数的个数。
但是这样做的问题就是要不断往前遍历,甚至运气不好降序排列的话就是n方*n了。所以我做着做着发现可以换个思路,就是直接确定某个数可以是第几位的子序。并且如果2 5 7,这个时候出现了3,把5替换成3.变成了2,3,7。以后再有数字如果是大于7的,比如8,9,10 该往后续就往后续。但是如果是4,也可以续在23的后面,子序变成了2,3,4。这样哪怕后面再出现5,最开始的2 5 7是不能续了,但是这里的2,3,4就可以续上5,变成了2,3,4,5这样的子序。可以保证一次遍历下来获取的是最长子序。
其实时间复杂度也就那样,我感觉会比dp稍微好点。并且我上面的代码提交性能超过百分之百。0ms,所以就这样了?
这个题我觉得dp是没问题的,不然我再用dp做一次?就当是复习知识了。
dp实现了,反正性能不咋地,也不知道是我处理的有问题还是怎么样,但是我个人感觉dp性能不如上面的那个也是正常的,我直接贴代码:
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length==0) return 0;
int[] d = new int[nums.length];
d[0] = 1;
int res = 1;
for(int i = 1;i因为做的比较无脑,总体来讲就是一个元素所有比他小的都可以+1个子序。然后遍历前面的所有选择一个最大值来判断。其实这么想也是n方的实现。。。
题目说还能NlogN。一说log我就想起来二分法了。。。其实我感觉我第一种实现方式因为确定新建数组是排好序的了,确实可以用二分法或者双指针定位当前元素大小处于哪个位置。。不过我就懒得改了, 这道题做了一个多小时快两个小时了,我直接下一题了。
二维区域和检索-矩形不可变
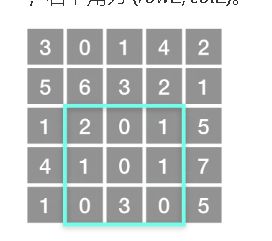
题目:给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。
示例:
给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
说明:
你可以假设矩阵不可变。
会多次调用 sumRegion 方法。
你可以假设 row1 ≤ row2 且 col1 ≤ col2。
思路:如图所示,我觉得重点有两个:一个是矩形不可变,一个是这个方法会多次调用,所以我目前的想法是在初始化的时候就对这个矩形进行计算操作。然后每次调用这个方法的时候使得计算量大大的减少。至于怎么计算我再看看题。我目前的想法是横着压缩或者竖着压缩。然后真正判断的时候确定这个矩形是较短的边,然后两端相减再一层一层相加。肯定比现在这样全遍历要效果好,但是是不是最优解,是不是leetcode想要的解我不知道。我先去试试了。
额,反正实现是实现了,性能没及格,但是真的测试案例绝了,我先贴代码:
class NumMatrix {
int[][] rows;
boolean isLive;
public NumMatrix(int[][] matrix) {
if(matrix.length==0 || matrix[0].length==0) isLive = true;
if(!isLive){
rows = new int[matrix.length][matrix[0].length];
int r = 0;
for(int i = 0;i这个我觉得已经是简单的了。剩下的看性能排行第一的代码了:
class NumMatrix {
int[][] dp;
public NumMatrix(int[][] matrix) {
if( matrix == null
|| matrix.length == 0
|| matrix[0].length == 0 ){
return;
}
dp = new int[matrix.length + 1][matrix[0].length + 1];
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j- 1] - dp[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
}
}
人家第一不冤,我是单纯的一个方向压缩,人家是横竖都压缩了。但是这个题我感觉没啥难点,就是判断边界。剩下的都是思路了,先压缩应该很容易想到,我直接下一题了。
累加数
题目:累加数是一个字符串,组成它的数字可以形成累加序列。一个有效的累加序列必须至少包含 3 个数。除了最开始的两个数以外,字符串中的其他数都等于它之前两个数相加的和。给定一个只包含数字 '0'-'9' 的字符串,编写一个算法来判断给定输入是否是累加数。说明: 累加序列里的数不会以 0 开头,所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。
示例 1:
输入: "112358"
输出: true
解释: 累加序列为: 1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8
示例 2:
输入: "199100199"
输出: true
解释: 累加序列为: 1, 99, 100, 199。1 + 99 = 100, 99 + 100 = 199
进阶:
你如何处理一个溢出的过大的整数输入?
思路:先不说溢出。这个题我觉得重点是选择第一个数和第二个数。然后我打算用回溯来试试。首先第一位是第一个数,然后第二个数的位数从头判断到不溢出的尾。都不行就前两位是第一个数,然后继续那么判断。反正最终有true的就true,都遍历完还没true就是false。这个时间复杂度比较高,应该是n方。但是目前没有别的好思路了,我去写代码了。对了,题目说最少包含三个数,所以前两个数的和是第三个数,所以第二位数不用从头到尾,确定不会超过数组的一半到三分之一就行。然后第一个数也不会超过数组的二分之一。反正这个值比较不好算,我先去代码试试。多了也没事,只不过是多做无用功而已。
emmmm....终于过了!调试的死去活来的恶心~!我先贴代码;
class Solution {
boolean flag;
public boolean isAdditiveNumber(String num) {
if(num.length()<3) return false;
int n = num.length()/2;
int m = (num.length()/3)*2;
long a = 0l;
long b = 0l;
for(int i = 0;i<=n;i++){
if(i>0 && num.charAt(0)=='0') break;
a = a*10+(num.charAt(i)-'0');
for(int j = i+1;j<=m;j++){
if(j>i+1 && num.charAt(i+1)=='0') break;
b = b*10+(num.charAt(j)-'0');
if(isAdditive(num.substring(j+1),a,b) && flag) return true;
}
b = 0;
}
return false;
}
private boolean isAdditive(String remain, long num1, long num2) {
if (remain.equals("")) return true;
long sum = num1 + num2;
String str = String.valueOf(sum);
if (!remain.startsWith(str)) return false;
flag = true;
return isAdditive(remain.substring(str.length()), num2, sum);
}
}
首先思路是对的,其次是这里不要直接把整个字符串拆成两部分!虽然这个条件判断差不多合理的,但是比如111这种只有三个数的时候,就会出问题。然后我加了个flag判断。
额,现在我发现可能是我范围取值不应该用小于等于。毕竟长度本身就比下标多了1 。改了一下,提交后还是对的,然后再贴一下代码:
class Solution {
public boolean isAdditiveNumber(String num) {
if(num.length()<3) return false;
int n = num.length()/2;
int m = (num.length()/3)*2;
long a = 0l;
long b = 0l;
for(int i = 0;i0 && num.charAt(0)=='0') break;
a = a*10+(num.charAt(i)-'0');
for(int j = i+1;ji+1 && num.charAt(i+1)=='0') break;
b = b*10+(num.charAt(j)-'0');
if(isAdditive(num.substring(j+1),a,b)) return true;
}
b = 0;
}
return false;
}
private boolean isAdditive(String remain, long num1, long num2) {
if (remain.equals("")) return true;
long sum = num1 + num2;
String str = String.valueOf(sum);
if (!remain.startsWith(str)) return false;
return isAdditive(remain.substring(str.length()), num2, sum);
}
}
这个题思路蛮清楚的,就是细节多调试一下就行了,我也是面向测试案例不断调试,反正最后成功了!
然后今天的笔记就记到这里,如果稍微帮到你了记得点个喜欢点个关注。也祝大家工作顺顺利利!生活健健康康!顺便打个广告:java技术交流群:130031711,欢迎大家踊跃加入!