数据结构和算法（6）队列的操作和实现

数据结构和算法（1）线性表实现

数据结构和算法（2）单向循环链表的创建插入删除实现

数据结构和算法（3）双向链表与双向循环链表的实现

数据结构和算法（4）链表相关面试题

数据结构和算法（5）栈和队列的操作和实现

数据结构和算法（6）队列的操作和实现

@[TOC]

1. 数据结构和算法（6）队列的操作和实现

代码下载

本篇博客代码下载：

• 队列的顺序存储操作
• 队列的链式存储操作

1.1 队列简介

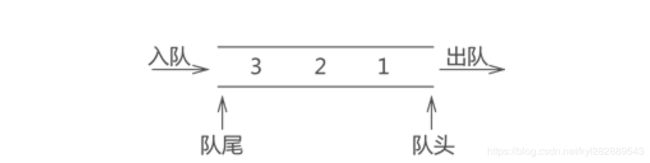
队列是一种先进先出(First In First Out)的线性表，也就是FIFO。通常，称进数据的一端为 "队尾"，出数据的一端为 "队头"，数据元素进队列的过程称为 "入队"，出队列的过程称为 "出队"。

与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出，如下图 所示：

如果对栈结构不熟悉可以参考我之前的博客：“数据结构和算法（五）栈和队列的操作和实现”

队列的存储结构

不仅如此，队列中数据的进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列。拿图 1 中的队列来说，从数据在队列中的存储状态可以分析出，元素 1 最先进队，其次是元素 2，最后是元素 3。此时如果将元素 3 出队，根据队列 "先进先出" 的特点，元素 1 要先出队列，元素 2 再出队列，最后才轮到元素 3 出队列。

栈和队列不要混淆，栈结构是一端封口，特点是"先进后出"；而队列的两端全是开口，特点是"先进先出"。

因此，数据从表的一端进，从另一端出，且遵循 "先进先出" 原则的线性存储结构就是队列。

队列存储结构的实现有以下两种方式：

1. 顺序队列：在顺序表的基础上实现的队列结构；
2. 链队列：在链表的基础上实现的队列结构；
   两者的区别仅是顺序表和链表的区别，即在实际的物理空间中，数据集中存储的队列是顺序队列，分散存储的队列是链队列。

实际生活中，队列的应用随处可见，比如排队买 XXX、医院的挂号系统等，采用的都是队列的结构。

拿排队买票来说，所有的人排成一队，先到者排的就靠前，后到者只能从队尾排队等待，队中的每个人都必须等到自己前面的所有人全部买票成功并从队头出队后，才轮到自己买票。这就不是典型的队列结构吗？

明白了什么是队列，接下来开始学习顺序队列和链队列的基本实现和注意事项。

1.2 队列顺序存储

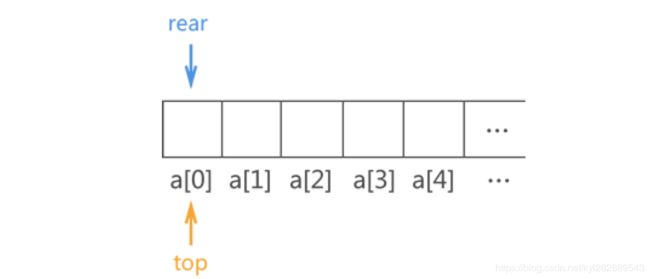
由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素，如下图 所示：

顺序队列的实现

由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

举个栗子：

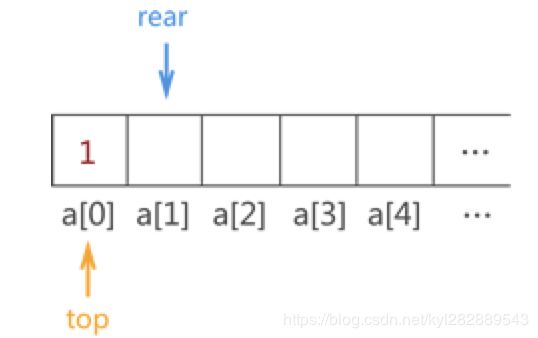
如果我们要将 {1,2,3,4} 用顺序队列存储的实现，

元素1 进队的过程如下：

元素1 入队

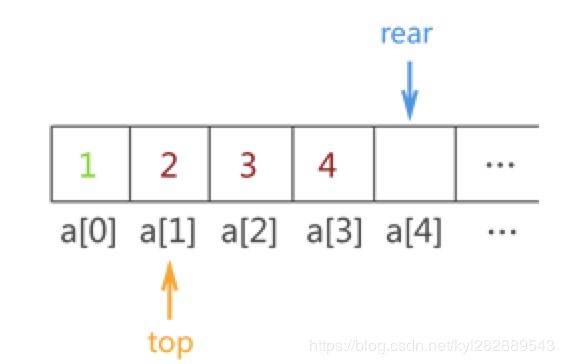
元素4入队过程：

元素4入队

那么我们接下来要将1，2，3，4这四个元素出队。出队过程如下：

元素1出队

元素4出队：

元素4出队

我们先看一下一个简单的顺序队列操作代码：

#include 

 int enQueue(int *a,int rear,int data){
     a[rear]=data;
     rear++;
     return rear;
 }
void deQueue(int *a,int front,int rear){
//如果 front==rear，表示队列为空
    while (front!=rear) {
        printf("出队元素：%d\n",a[front]);
         front++;
     }
 }
 
int main() {
    int a[100];
    int front,rear;
    //设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址
    front=rear=0;
    //入队
    rear=enQueue(a, rear, 1);
    rear=enQueue(a, rear, 2);
    rear=enQueue(a, rear, 3);
    rear=enQueue(a, rear, 4);
    //出队
    deQueue(a, front, rear);
    return 0;
 }

输出结构为：

出队元素：1
出队元素：2
出队元素：3
出队元素：4

上面这种顺序存储队列会存在一些问题，如假溢出问题，如下图：

顺序队列假溢出问题

如上图，我们先将A，B，C三个元素依次入队，然后将A,B 出队，然后又入队了D，E，元素，这个时候rear队尾指针指向了数组的最后，实际上我们还有两个空间可以利用，这个时候队列并没有满，但是由于rear指向了最后，也就是顺序队列整体发生了后移，这样造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；也就是假溢出。
• 另外如如果顺序表申请的空间不足够大，则直接造成程序中数组溢出，产生溢出错误；

为了解决上面问题，我们有一种比较优的解决办法，就是用循环队列来解决假溢出问题。

接下来将介绍循环队列。

1.2.1 循环队列

循环队列就是，当队尾指针移动到数组末尾时，下次再有元素入队时，可以将队尾指针重新移到数组前面没有元素的位置。

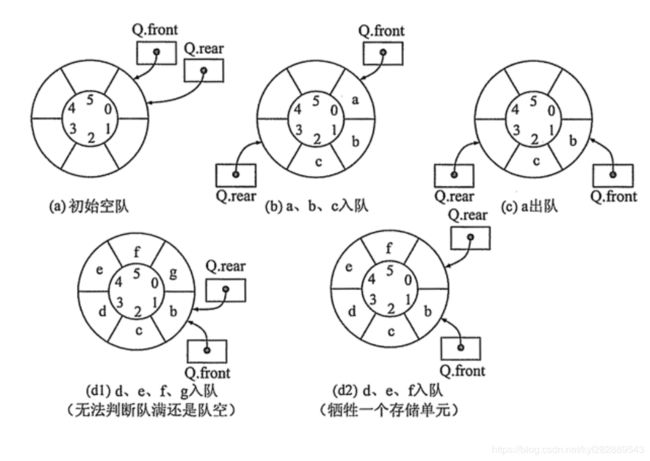
循环队列操作如下图：

循环队列解决假溢出问题

如上图：
（a） 我们用Q.front == Q.rear表示队列为空。
当我们依次入队a,b,c三个元素后，如上图(b)所示。
接下来，我们将元素a 从队头出队，如上图(c)所示。
然后，我们又依次入队了d ,e ,f, g这个时候实际上队列已经存满了，单我们发现 Q.front == Q.rear，如上图(d1)所示。但是我们前面(a)中用Q.front == Q.rear表示队列为空，但是队列满了的时候我们Q.front == Q.rear就无法区分到底是队列为空还是满了。为了解决这个问题，我们一般采用牺牲一个存储空间的方式。也就如上图(d2) 我们用Q.front = Q.rear + 1表示堆满，就是牺牲一个存储单元不存放数据。

在循环队列中我们判断队列为空，队列为满的条件如下：

1. 队列为满： (Q.rear+1)％maxSize==Q.front
2. 队列为空： Q.rear==Q.front
3. 队列中有效的数据的个数： (Q.rear+maxSize-Q.front)%maxSize

1.2.2 循环队列的代码实现

• 循环队列的顺序存储结构

/* 循环队列的顺序存储结构 */
typedef struct KQueue
{
    KQueueElementType data[MAXSIZE];
    int front;        /* 头指针 */
    int rear;        /* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}KQueue;

1.2.2.1 初始化

//1. 初始化一个队列
KStatus initQueue(KQueue *Q) {
    Q->front = Q->rear = 0;
    return OK;
}

1.2.2.2 队列清空

//2. 将队列清空
KStatus clearQueue(KQueue *Q) {
    Q->front = Q->rear = 0;
    return OK;
}

1.2.2.3 队列判空

//3. 队列判空
KStatus isEmpty(KQueue Q) {
    return Q.front == Q.rear ;
}

1.2.2.4 队列是否满了

//4. 队列是否满了
KStatus isFull(KQueue Q) {
    return Q.front == (Q.rear + 1 ) % MAXSIZE;
}

1.2.2.5 查询队列长度

//5. 查询队列长度
int getLength(KQueue Q) {
    return (Q.rear - Q.front + MAXSIZE)%MAXSIZE;
}

1.2.2.6 获取队头元素

//6. 获取队头元素
//若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR;
KStatus getHead(KQueue Q, KQueueElementType *e) {
    //判断是否队列为空
    if (isEmpty(Q)) {
        return ERROR;
    }
    //取出元素值
    *e = Q.data[Q.front];
    return OK;
}

1.2.2.7 入队

//7. 入队
// 若队列未满,则插入元素e为新队尾元素
KStatus enQueue(KQueue *Q, KQueueElementType e) {
    //判断队列是否满了
    if (isFull(*Q)) {
        return ERROR;
    }
    //将元素e赋值给队尾
    Q->data[Q->rear] = e;
    
    //rear指针向后移动一位，若到最后则转到数组头部
    Q->rear = (Q->rear + 1) % MAXSIZE;
    
    return OK;
}

1.2.2.8 出队

//8. 出队
//若队列不空,则删除Q中队头的元素,用e返回值
KStatus deQueue(KQueue *Q, KQueueElementType *e) {
    if (isEmpty(*Q)) return ERROR;
    //从队头取出元素赋值给e
    *e = Q->data[Q->front];
    
    //front指针向后移动一位，删除对头元素
    Q->front = (Q->front + 1) % MAXSIZE;
    
    return OK;
}

1.2.2.9 遍历队列

//9. 遍历队列
KStatus traverseQueue(KQueue Q) {
    int i = Q.front;
    while ((i + Q.front) != Q.rear) {
        //从队头遍历到队尾，依次输出元素，i表示当前已经输出到第几个元素了
        //(i + Q.front) != Q.rear 表示 已经遍历到了队尾了，
        //由于我们不能修改front和rear指向，所以需要一个临时变量记录当前位置
        printf("%d  ", Q.data[I]);
        i = (i + 1) % MAXSIZE;
    }
    printf("\n");
    
    return OK;
}

1.2.2.10 单元测试

//10. 单元测试
void test() {
    printf("循环队列操作单元测试\n");
    KStatus j;
    int I=0;
    KQueueElementType d;
    KQueue Q;
    initQueue(&Q);
    printf("初始化队列后，队列空否？%u(1:空 0:否)\n",isEmpty(Q));
    
    printf("入队:\n");
    while (i < 10) {
        enQueue(&Q, i);
        I++;
    }
    traverseQueue(Q);
    printf("队列长度为: %d\n",getLength(Q));
    printf("现在队列空否？%u(1:空 0:否)\n",isEmpty(Q));
    printf("出队:\n");
   
   //出队
    deQueue(&Q, &d);
    printf("出队的元素:%d\n",d);
    traverseQueue(Q);

    //获取队头
    j=getHead(Q,&d);
    if(j)
        printf("现在队头元素为: %d\n",d);
    clearQueue(&Q);
    printf("清空队列后, 队列空否？%u(1:空 0:否)\n",isEmpty(Q));

}

1.2.2.11 完整代码

//
//  main.c
//  010_Queue
//
//  Created by 孔雨露 on 2020/4/18.
//  Copyright © 2020 Apple. All rights reserved.
//

#include 
#include "stdlib.h"
#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int KStatus;
typedef int KQueueElementType; /* KQueueElementType类型根据实际情况而定，这里假设为int */

/* 循环队列的顺序存储结构 */
typedef struct KQueue
{
    KQueueElementType data[MAXSIZE];
    int front;        /* 头指针 */
    int rear;        /* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}KQueue;

//1. 初始化一个队列
KStatus initQueue(KQueue *Q) {
    Q->front = Q->rear = 0;
    return OK;
}

//2. 将队列清空
KStatus clearQueue(KQueue *Q) {
    Q->front = Q->rear = 0;
    return OK;
}

//3. 队列判空
KStatus isEmpty(KQueue Q) {
    return Q.front == Q.rear ;
}

//4. 队列是否满了
KStatus isFull(KQueue Q) {
    return Q.front == (Q.rear + 1 ) % MAXSIZE;
}

//5. 查询队列长度
int getLength(KQueue Q) {
    return (Q.rear - Q.front + MAXSIZE)%MAXSIZE;
}

//6. 获取队头元素
//若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR;
KStatus getHead(KQueue Q, KQueueElementType *e) {
    //判断是否队列为空
    if (isEmpty(Q)) {
        return ERROR;
    }
    //取出元素值
    *e = Q.data[Q.front];
    return OK;
}

//7. 入队
// 若队列未满,则插入元素e为新队尾元素
KStatus enQueue(KQueue *Q, KQueueElementType e) {
    //判断队列是否满了
    if (isFull(*Q)) {
        return ERROR;
    }
    //将元素e赋值给队尾
    Q->data[Q->rear] = e;
    
    //rear指针向后移动一位，若到最后则转到数组头部
    Q->rear = (Q->rear + 1) % MAXSIZE;
    
    return OK;
}

//8. 出队
//若队列不空,则删除Q中队头的元素,用e返回值
KStatus deQueue(KQueue *Q, KQueueElementType *e) {
    if (isEmpty(*Q)) return ERROR;
    //从队头取出元素赋值给e
    *e = Q->data[Q->front];
    
    //front指针向后移动一位，删除对头元素
    Q->front = (Q->front + 1) % MAXSIZE;
    
    return OK;
}

//9. 遍历队列
KStatus traverseQueue(KQueue Q) {
    int i = Q.front;
    while ((i + Q.front) != Q.rear) {
        //从队头遍历到队尾，依次输出元素，i表示当前已经输出到第几个元素了
        //(i + Q.front) != Q.rear 表示 已经遍历到了队尾了，
        //由于我们不能修改front和rear指向，所以需要一个临时变量记录当前位置
        printf("%d  ", Q.data[I]);
        i = (i + 1) % MAXSIZE;
    }
    printf("\n");
    
    return OK;
}


//10. 单元测试
void test() {
    printf("循环队列操作单元测试\n");
    KStatus j;
    int I=0;
    KQueueElementType d;
    KQueue Q;
    initQueue(&Q);
    printf("初始化队列后，队列空否？%u(1:空 0:否)\n",isEmpty(Q));
    
    printf("入队:\n");
    while (i < 10) {
        enQueue(&Q, i);
        I++;
    }
    traverseQueue(Q);
    printf("队列长度为: %d\n",getLength(Q));
    printf("现在队列空否？%u(1:空 0:否)\n",isEmpty(Q));
    printf("出队:\n");
   
   //出队
    deQueue(&Q, &d);
    printf("出队的元素:%d\n",d);
    traverseQueue(Q);

    //获取队头
    j=getHead(Q,&d);
    if(j)
        printf("现在队头元素为: %d\n",d);
    clearQueue(&Q);
    printf("清空队列后, 队列空否？%u(1:空 0:否)\n",isEmpty(Q));

}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    test();
    return 0;
}

• 单元测试，输出结果：

Hello, World!
循环队列操作单元测试
初始化队列后，队列空否？1(1:空 0:否)
入队:
0  1  2  3  4  5  6  7  8  9  
队列长度为: 10
现在队列空否？0(1:空 0:否)
出队:
出队的元素:0
1  2  3  4  5  6  7  8  
现在队头元素为: 1
清空队列后, 队列空否？1(1:空 0:否)
Program ended with exit code: 0

1.3 队列链式存储

链式队列的实现思想同顺序队列类似，只需创建两个指针（命名为 top 和 rear）分别指向链表中队列的队头元素和队尾元素，如图下图1 所示:

图 1 链式队列的初始状态

图 1 所示为链式队列的初始状态，此时队列中没有存储任何数据元素，因此 top 和 rear 指针都同时指向头节点。

下面我们来讲解一下 链式队列入队，出队操作，链式队列入队，出队操作基本跟单链表相似，如果不熟悉链表的操作可以参考我之前的链表相关的博客：

1. "数据结构和算法（一）线性表实现"
2. “数据结构和算法（二）单链表与单向循环链表的实现”

基本就是入队就是在链表尾部结点插入一个元素，出队就是在链表头结点删除一个结点。

• 链式队列入队操作：
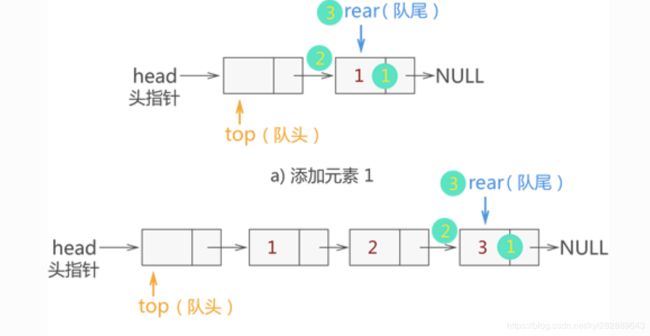
  如下图2 表示链式队列依次入队{1，2，3} 三个元素：

图 2 {1,2,3} 入链式队列

如上图所示，在链队队列中，当有新的数据元素入队，只需进行以下 3 步操作：

1. 将该数据元素用节点包裹，例如新节点名称为 elem；
2. 与 rear 指针指向的节点建立逻辑关系，即执行 rear->next=elem；
3. 最后移动 rear 指针指向该新节点，即 rear=elem；

• 链式队列出队操作：
  当链式队列中，有数据元素需要出队时，按照 "先进先出" 的原则，只需将存储该数据的节点以及它之前入队的元素节点按照原则依次出队即可。出队过程就是从链表头依次删除首结点的过程, 现在我们需要将上图2中的1，2 两个元素出队，其操作过程 如下图3所示：

图 3 链式队列中数据元素出队

如上图3所示，我们可以知道，在链式队列中队头元素出队，需要做以下 3 步操作：

1. 通过 top 指针直接找到队头节点，创建一个新指针 p 指向此即将出队的节点；
2. 将 p 节点（即要出队的队头节点）从链表中摘除；
3. 释放节点 p，回收其所占的内存空间；

1.3.2 队列链式存储的代码实现

• 链式队列的结构定义

//结点结构
typedef struct KQueueNode{
    KQueueElementType data;
    struct KQueueNode *next;
}KQNode, *KQueuePtr;

//队列的链表结构
typedef struct KLinkQueue {
    KQueuePtr front; //队头
    KQueuePtr rear;  //队尾
}KLQueue;

1.3.2.1 初始化

// 1. 初始化队列
KStatus initQueue(KLQueue *Q) {
    //1. 队列头指针和尾指针都只需新生成的结点
    Q->front = Q->rear = (KQueuePtr)malloc(sizeof(KQNode));
    //2. 判断结点是否创建成功
    if (!Q->front) return ERROR;
    //3. 队列头指针域置空
    Q->front->next = NULL;
    
    return OK;
}

1.3.2.2 销毁队列

// 2. 销毁队列
KStatus destoryQueue(KLQueue *Q) {
    //遍历整个队列，销毁每一个结点
    while (Q->front) {
        Q->rear = Q->front->next;
        free(Q->front);
        Q->front = Q->rear;
    }
    return OK;
}

1.3.2.3 清空队列

// 3. 清空队列
KStatus clearQueue(KLQueue *Q) {
    KQueuePtr p,q;
    Q->rear = Q->front;
    p = Q->front->next;
    Q->front->next = NULL;
    while (p) {
        q = p->next;
        p = p->next;
        free(q);
    }
    return OK;
}

1.3.2.4 队列判空

// 4. 队列判空
KStatus isEmpty(KLQueue Q) {
    return Q.front == Q.rear;
}

1.3.2.5 获取对头元素

// 6. 获取对头元素
KStatus getHead(KLQueue Q, KQueueElementType *e){
    if (Q.front != Q.rear) {
        //返回队头元素的值,队头指针不变
        *e = Q.front->next->data;
        return TRUE;
    }
    
    return FALSE;
}

1.3.2.6 获取队列长度

// 7. 获取队列长度
int getLength(KLQueue Q){
    int count = 0;
    KQueuePtr p = Q.front;
    while (Q.rear != p) {
        count++;
        p = p->next;
    }
    return count;
}

1.3.2.7 入队

// 8. 入队
KStatus enQueue(KLQueue *Q, KQueueElementType e) {
    //为入队元素分配结点空间,用指针s指向;
    KQueuePtr s = (KQueuePtr)malloc(sizeof(KQNode));
    if (!s) return ERROR;
    //将新结点s指定数据域
    s->data = e;
    s->next = NULL;
    
    //将新结点插入到队列尾部
    Q->rear->next = s;
    //修改队尾指针
    Q->rear = s;
    
    return OK;
}

1.3.2.8 出队

// 9. 出队
KStatus deQueue(KLQueue *Q, KQueueElementType *e) {
    KQueuePtr p;
    //判断队列是否为空
    if (isEmpty(*Q)) return ERROR;
    
    //将要删除的队头结点暂时存储在p
    p = Q->front->next;
    //将要删除的队头结点的值赋值给e
    *e = p->data;
    //将原队列头结点的后继p->next 赋值给头结点后继
    Q->front->next = p->next;
    
    //若队头就是队尾,则删除后将rear指向头结点.
    if(Q->rear == p) Q->rear = Q->front;
    
    //释放结点
    free(p);
    
    return OK;
}

1.3.2.9 遍历队列

// 10. 遍历队列
KStatus traverseQueue(KLQueue Q) {
    KQueuePtr p = Q.front->next;
    while (p) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
    
    return OK;
}

1.3.2.10 单元测试

// 11. 单元测试
void test() {
    printf("链队列的表示与操作!\n");
    
    KStatus iStatus;
    KQueueElementType d;
    KLQueue q;
    
    //1.初始化队列q
    iStatus = initQueue(&q);
    
    //2. 判断是否创建成
    if (iStatus) {
        printf("成功地构造了一个空队列\n");
    }
    
    //3.判断队列是否为空
    printf("是否为空队列?%d (1:是 0:否)\n",isEmpty(q));
    
    //4.获取队列的长度
    printf("队列的长度为%d\n",getLength(q));
    
    //5.插入元素到队列中
    enQueue(&q, -3);
    enQueue(&q, 6);
    enQueue(&q, 12);
    
    printf("队列的长度为%d\n",getLength(q));
    printf("是否为空队列?%d (1:是 0:否)\n",isEmpty(q));
    
    //6.遍历队列
    printf("队列中的元素如下:\n");
    traverseQueue(q);

    //7.获取队列头元素
    iStatus = getHead(q, &d);
    if (iStatus == OK) {
        printf("队头元素是:%d\n",d);
    }
    
    //8.删除队头元素
    iStatus = deQueue(&q, &d);
    if (iStatus == OK) {
        printf("删除了的队头元素为:%d\n",d);
    }
    
    //9.获取队头元素
    iStatus = getHead(q, &d);
    if (iStatus == OK) {
        printf("新的队头元素为:%d\n",d);
    }
    
    //10.清空队列
    clearQueue(&q);
    
    //11.销毁队列
    destoryQueue(&q);
}

• 单元测试，输出结果：

Hello, World!
链队列的表示与操作!
成功地构造了一个空队列
是否为空队列?1 (1:是 0:否)
队列的长度为0
队列的长度为3
是否为空队列?0 (1:是 0:否)
队列中的元素如下:
-3 6 12 
队头元素是:-3
删除了的队头元素为:-3
新的队头元素为:6
Program ended with exit code: 0

1.3.2.11 完整代码

//
//  main.c
//  011_LinkQueue
//
//  Created by 孔雨露 on 2020/4/18.
//  Copyright © 2020 Apple. All rights reserved.
//

/*
 链式 队列的基本操作实现
 */

#include 
#include "stdlib.h"
#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20

typedef int KStatus;
typedef int KQueueElementType;

//结点结构
typedef struct KQueueNode{
    KQueueElementType data;
    struct KQueueNode *next;
}KQNode, *KQueuePtr;

//队列的链表结构
typedef struct KLinkQueue {
    KQueuePtr front; //队头
    KQueuePtr rear;  //队尾
}KLQueue;

// 1. 初始化队列
KStatus initQueue(KLQueue *Q) {
    //1. 队列头指针和尾指针都只需新生成的结点
    Q->front = Q->rear = (KQueuePtr)malloc(sizeof(KQNode));
    //2. 判断结点是否创建成功
    if (!Q->front) return ERROR;
    //3. 队列头指针域置空
    Q->front->next = NULL;
    
    return OK;
}

// 2. 销毁队列
KStatus destoryQueue(KLQueue *Q) {
    //遍历整个队列，销毁每一个结点
    while (Q->front) {
        Q->rear = Q->front->next;
        free(Q->front);
        Q->front = Q->rear;
    }
    return OK;
}

// 3. 清空队列
KStatus clearQueue(KLQueue *Q) {
    KQueuePtr p,q;
    Q->rear = Q->front;
    p = Q->front->next;
    Q->front->next = NULL;
    while (p) {
        q = p->next;
        p = p->next;
        free(q);
    }
    return OK;
}

// 4. 队列判空
KStatus isEmpty(KLQueue Q) {
    return Q.front == Q.rear;
}


// 6. 获取对头元素
KStatus getHead(KLQueue Q, KQueueElementType *e){
    if (Q.front != Q.rear) {
        //返回队头元素的值,队头指针不变
        *e = Q.front->next->data;
        return TRUE;
    }
    
    return FALSE;
}

// 7. 获取队列长度
int getLength(KLQueue Q){
    int count = 0;
    KQueuePtr p = Q.front;
    while (Q.rear != p) {
        count++;
        p = p->next;
    }
    return count;
}


// 8. 入队
KStatus enQueue(KLQueue *Q, KQueueElementType e) {
    //为入队元素分配结点空间,用指针s指向;
    KQueuePtr s = (KQueuePtr)malloc(sizeof(KQNode));
    if (!s) return ERROR;
    //将新结点s指定数据域
    s->data = e;
    s->next = NULL;
    
    //将新结点插入到队列尾部
    Q->rear->next = s;
    //修改队尾指针
    Q->rear = s;
    
    return OK;
}

// 9. 出队
KStatus deQueue(KLQueue *Q, KQueueElementType *e) {
    KQueuePtr p;
    //判断队列是否为空
    if (isEmpty(*Q)) return ERROR;
    
    //将要删除的队头结点暂时存储在p
    p = Q->front->next;
    //将要删除的队头结点的值赋值给e
    *e = p->data;
    //将原队列头结点的后继p->next 赋值给头结点后继
    Q->front->next = p->next;
    
    //若队头就是队尾,则删除后将rear指向头结点.
    if(Q->rear == p) Q->rear = Q->front;
    
    //释放结点
    free(p);
    
    return OK;
}


// 10. 遍历队列
KStatus traverseQueue(KLQueue Q) {
    KQueuePtr p = Q.front->next;
    while (p) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
    
    return OK;
}

// 11. 单元测试
void test() {
    printf("链队列的表示与操作!\n");
    
    KStatus iStatus;
    KQueueElementType d;
    KLQueue q;
    
    //1.初始化队列q
    iStatus = initQueue(&q);
    
    //2. 判断是否创建成
    if (iStatus) {
        printf("成功地构造了一个空队列\n");
    }
    
    //3.判断队列是否为空
    printf("是否为空队列?%d (1:是 0:否)\n",isEmpty(q));
    
    //4.获取队列的长度
    printf("队列的长度为%d\n",getLength(q));
    
    //5.插入元素到队列中
    enQueue(&q, -3);
    enQueue(&q, 6);
    enQueue(&q, 12);
    
    printf("队列的长度为%d\n",getLength(q));
    printf("是否为空队列?%d (1:是 0:否)\n",isEmpty(q));
    
    //6.遍历队列
    printf("队列中的元素如下:\n");
    traverseQueue(q);

    //7.获取队列头元素
    iStatus = getHead(q, &d);
    if (iStatus == OK) {
        printf("队头元素是:%d\n",d);
    }
    
    //8.删除队头元素
    iStatus = deQueue(&q, &d);
    if (iStatus == OK) {
        printf("删除了的队头元素为:%d\n",d);
    }
    
    //9.获取队头元素
    iStatus = getHead(q, &d);
    if (iStatus == OK) {
        printf("新的队头元素为:%d\n",d);
    }
    
    //10.清空队列
    clearQueue(&q);
    
    //11.销毁队列
    destoryQueue(&q);
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    test();
    return 0;
}