《代码本色：用编程模拟自然系统》习作——第1章：向量

前言

近日拜读了Daniel Shiffman先生的著作——《代码本色：用编程模拟自然系统》，决定做一组习作，来对书中提到的随机行为及牛顿运动学进行理解，并对一些实例进行拓展学习，从而提升自己相关方面的知识水平和实践能力。

《代码本色》第1章概述

在第1章中，作者向我们介绍了"向量"这一概念，在Processing中，向量的使用非常关键。本章包含了向量的加法、减法、乘法、归一化等基本知识。作者用BallBounce这个例子来讲述PVector的一些用法，使人耳目一新。

习作和创作过程

由于之前自学过相关知识，并已经在之前的一次作业中使用过PVector，实现了鼠标跟随的功能，在本文中就对当时的创作进行简短的回顾。
随后，我又根据书中向量的一些加减法，制作了一个交互式的向量加减法可视化软件。

一群点跟随鼠标运动

那么首先，来回顾一下我之前做的作品吧：

前作

这个作品运用的物理知识在书中的第1.7节和1.8节中进行了介绍。该作品的主要代码如下：

class Point {
  PVector Position, speed, accelerate; 
  Point(){
  Position = new PVector(random(width), random(height));
  speed= new PVector();
  accelerate= new PVector();
  }
  void render(int R,int G,int B){
  fill(R,G,B);
  noStroke();
  ellipse(Position.x,Position.y,10,10);
  }
  void update(){
  accelerate = new PVector(mouseX-Position.x, mouseY -Position.y); 
  accelerate.limit(1);
  speed.add(accelerate);
  speed.limit(20);
  Position.add(speed);
  }
}
Point [] points = new Point[50];
void setup(){
  size(800,800);
  background(255);
  for( int i =0; i < points.length; i++){
    points[i] = new Point();
  }
}
void draw(){
  int a=millis()/10;
  int b=millis()/50;
  int c=millis()/100;
  fill(255,255,255,50);
  rect(0,0,800,800);
  for( int i =0; i < points.length; i++){
    points[i].update(); 
    points[i].render(c,b,a); 
  } 
}

可以看到，我建立了一个Point类，其中建立了Position, speed, accelerate三个PVector向量，并使用Limit函数限制他们的大小。然后根据鼠标位置和点的位置的差值计算加速度，然后将加速度累加给速度，速度累加给位置。就是这样的一个经典的跟随鼠标的算法。同时，使用millis（）函数获取了时间的变化，实现了颜色的平滑变化。

交互式向量计算与绘制——加法

首先，我参考1.41中向量的减法的示例编写了一个向量绘制的功能。
第一步，要画一条从屏幕中间到鼠标点的线——这听起来很简单，但是却有不少细节。我是以1.4.1向量的减法为例进行代码的编写的，因为这条线也可以理解成是鼠标位置的坐标向量与屏幕中心的坐标向量相减得出的结果。
代码如下：

  background(0);
  PVector mouse = new PVector(mouseX, mouseY);
  PVector center = new PVector(width/2, height/2);
  mouse.sub(center);
  translate(width/2, height/2);
  strokeWeight(2);
  stroke(255);
  line(0, 0, mouse.x, mouse.y);//画新的线

这里需要注意的是这一行

  translate(width/2, height/2);

这个代表什么呢？在之前的自画像文章中我提到过，translate函数表示在这一帧将坐标系平移一定的量。这里为什么要平移半个屏幕的宽和半个屏幕的高呢？这是因为mouseX和mouseY这两个变量都是根据屏幕左上角为原点的，而我们想要的是它以屏幕中心为原点，如果不加这一句，结果就会变成这样：

错误的示例.gif

可以看到，这个程序的确将鼠标位置和屏幕中心的差值计算出来了，但是却从原点开始画了。加上translate语句后，就解决了这个问题。

第二步，为了将每次画的点存下来，我使用了上一篇文章中介绍过了ArrayList数组：

ArrayListPoints=new ArrayList();

然后，编写了mouseClicked()函数，也就是说，每次点击鼠标，就可以添加一个新的点加入ArrayList：

void mouseClicked()
{
   PVector newPoint =new PVector();
  newPoint.x=mouseX-width/2;
  newPoint.y=mouseY-height/2;
  Points.add(newPoint);
  }

注意！这里的点也需要进行转换！！分别减去屏幕长的一半和宽的一半。
效果如下：

GIF2.gif

通过点击鼠标，就可以添加新的线了，非常方便。
那么下一步，我们就要进入正题了——计算这些向量的和向量。为此，我添加了一个新的交互方式——鼠标右键点击。
但由于之前编写的mouseClicked（）函数是不区分鼠标左右键的，为此，需要对mouseClicked函数的内容进行改写。
在Processing中，通常我们用mouseButton变量来判断我们按下的键位。LEFT为左键，RIGHT为右键，所以，我们将之前写的改成这样：

void mouseClicked()
{
  if(mouseButton == LEFT)
  {
   PVector newPoint =new PVector();
  newPoint.x=mouseX-width/2;
  newPoint.y=mouseY-height/2;
  Points.add(newPoint);
  }
}

然后，加入鼠标右键的相应内容：

void mouseClicked()
{
  if(mouseButton == LEFT)
  {
   PVector newPoint =new PVector();
  newPoint.x=mouseX-width/2;
  newPoint.y=mouseY-height/2;
  Points.add(newPoint);
  }
  if(mouseButton == RIGHT)
  {
    CalcTotalVector();
  }
}

可以看到，我将计算和向量的操作放到了 CalcTotalVector()函数中进行处理。 CalcTotalVector()函数的代码如下：

void CalcTotalVector()
{
PVector sum=new PVector();
  for(int i=0;i

实现效果如下：

GIF3.gif

可以看到，已经实现了正确的结果，上图中第四条最短的线就是前三个向量的和向量。但是由于我是直接将新的向量存入Points列表中，随意最后出来的线很难和之前的区分，于是我进行了改进。
首先，将新生成的点单独存取至一个全局变量中：

PVector sum=new PVector();

随后，在draw函数里添加下面这段代码：

  //画和向量
  stroke(255,255,0);
  line(0,0,sum.x,sum.y);

这样就可以画出颜色不同的线了，效果如下：

GIF4.gif

最后，为了让向量的显示更加直观，我使用text函数加入了文字标识，最终成品如下：

GIF5.gif

下面附上全部代码：

ArrayListPoints=new ArrayList();
PVector sum=new PVector();
void setup(){
  size(800,800);
}

void draw()
{
  background(0);
  PVector mouse = new PVector(mouseX, mouseY);
  PVector center = new PVector(width/2, height/2);
  mouse.sub(center);
  translate(width/2, height/2);
  strokeWeight(2);
  stroke(255);
  line(0, 0, mouse.x, mouse.y);//画新的线
  
  //画之前确认的线
  for(int i=0;i

交互式向量计算与绘制——减法

向量的减法原理在书中的定义如下：

向量减法

实现的过程和加法比较类似，这里就不详细的讲述了，最终实现的效果如下：

减法

下面附上代码：

ArrayListPoints=new ArrayList();
PVector sub=new PVector();
void setup(){
  size(800,800);
}

void draw()
{
  background(0);
  PVector mouse = new PVector(mouseX, mouseY);
  PVector center = new PVector(width/2, height/2);
  mouse.sub(center);
  translate(width/2, height/2);
  strokeWeight(2);
  stroke(255);
  line(0, 0, mouse.x, mouse.y);//画新的线
  
  //画之前确认的线
  for(int i=0;i

交互式向量计算与绘制——点乘

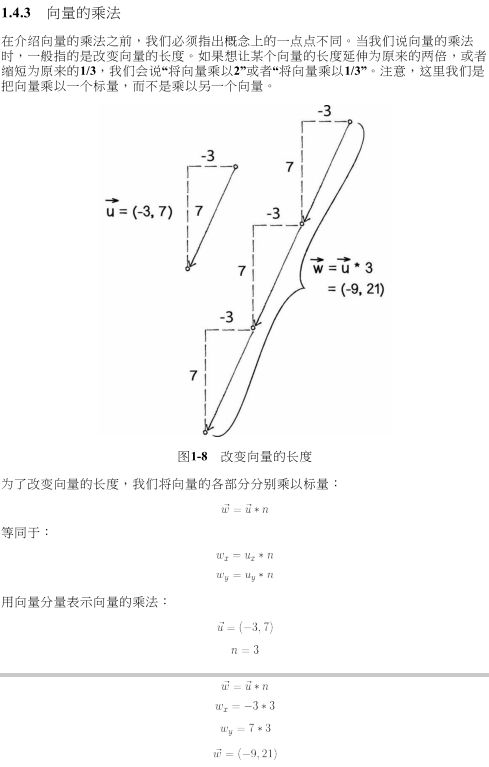
点乘的定义也比较好理解，相当于是每个元素都乘以一个常数，书中给出的定义如下：

点乘的定义

绘制系统的实现中，还是先画出一些向量，最后将它们的和点乘2，效果如下：

点乘

代码如下：

ArrayListPoints=new ArrayList();
PVector mul=new PVector();
PVector sum=new PVector();
void setup(){
  size(800,800);
}

void draw()
{
  background(0);
  PVector mouse = new PVector(mouseX, mouseY);
  PVector center = new PVector(width/2, height/2);
  mouse.sub(center);
  translate(width/2, height/2);
  strokeWeight(2);
  stroke(255);
  line(0, 0, mouse.x, mouse.y);//画新的线
  
  //画之前确认的线
  for(int i=0;i

总结

本文介绍了《代码本色：用编程模拟自然系统》第1章的主要内容，并在示例的基础上进行了拓展性的创作，创作了：鼠标跟随点的生成、交互式向量加法计算与绘制、交互式向量减法计算与绘制、交互式向量乘法计算与绘制。