教学安排
1. 绪论
2. 绪论之算法
3,4周线性表
5周-栈与队列
6周-递归与分治
7,8周-树与二叉树
9,10周-图论与贪心算法
11周-动态规划
12到16周-考试
程序= 数据结构+ 算法
算法= 逻辑+ 控制
例子:迷宫
字符界面/图形界面/交互界面--界面与问题的本质是没有关系的
入口到出口的通路?
输入? 迷宫地图/入口与出口
输出?入口到出口的路径
输入如何转化为输出? 算法
1. 如何表示给定的地图空间?/如何表示入口出口
用一个二维数组来表示迷宫空间,并约定 maze(i,j)=0 为通路/ maze(i,j)=0 为不通路
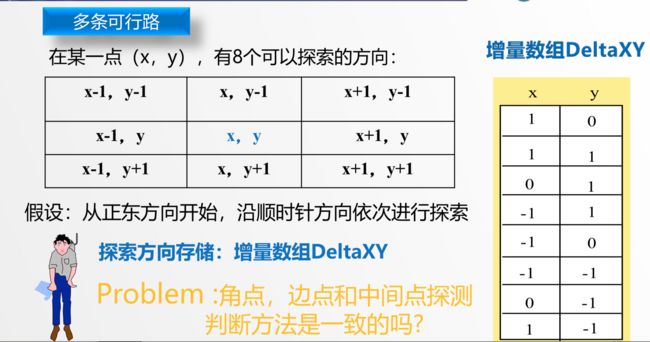
2.当有多条可行路径时如何选择?
是指一个规律,设某一点(x,y)
角点,边点和中间点的探测方法不一致--为了使探索方向个数一致,可在原来的迷宫地图四周围都扩展一个点,即 增加两行和两列,并将迷宫四周增加点的值全部置为1,表示是墙,不能通 行。
这样做使得原迷宫地图中的所有点都成为了中间点,不用再判断当前点是 角点、边点、还是中间点,每个点的探索方向均为8个。
3.探测过程中,当某一点没有再可行路径时应该如何处理?
栈!
回退到上一个具有多条路径的地方选择下一条路径探测; 需要存储每一个具有多条路径的点坐标和探索方向(x,y,d),存储的多个(x,y,d)选择最新存储位置回退•
4.如何判断某个位置是经过的还是没经过的?兜圈子问题
解决兜死圈子,有两种方法:
第一种:设置一个标志数组mark[m][n],所有元素初始化为0,在探索中,当所探索的点( i,j )对应的mark[i][j]=0时,才进入该点,并将mark[i][ j]置为1;
当所探索的点( i,j )对应的mark[i][j]=1时,表明已探索过,不需要再进入。
第二种. 当到达某点(i,j)后,在迷宫地图的该点坐标上标记特殊值,例如将maze[i][j] 置 -1,以便区别未到达过的点。
小结
数据结构的作用:
存放和处理数据:如迷宫地图
实现算法策略:如迷宫例子中探索方向增量数组、回溯的栈、避免重复走的标志数组或特殊标记)
eg.号码簿
数据结构设计-如何表示和存储电话号码
算法设计-如何实现快速查找
相关术语
Data数据-Data Object数据对象-Data Element数据元素-Data Item数据项
常见的数据结构
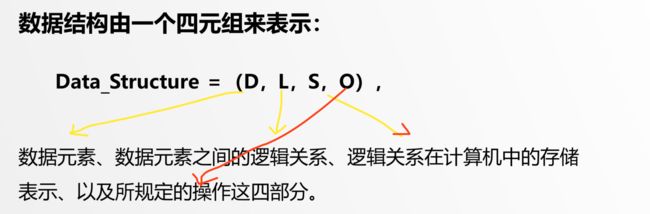
数据结构
数据结构
存储结构的分类
五类:顺序存储结构 链式存储结构
****以上所有内容均来自 中国大学MOOC 电子科技大学 数据结构与算法 戴波 林勋 刘震