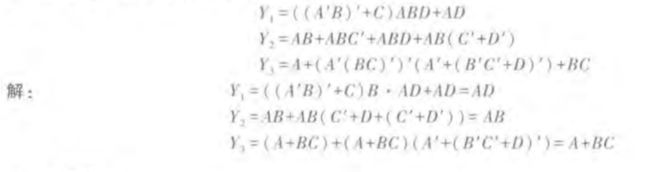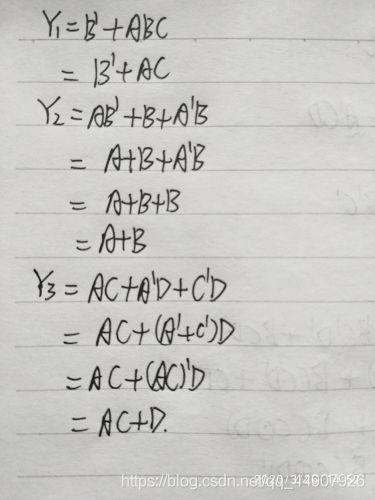数字电子技术第二章(逻辑代数基础)(2)
《 数字电子技术第6版》
2.5逻辑函数及其描述方法
举个引入的粟子:
如果以逻辑变量作为输入,以运算结果作为输出,那么当输入变量的取值确定之后,输出的取值便随之而定。因此,输出与输入之间乃是一种函数关系。这种函数关系称为逻辑函数,写作:
Y = F(A,B,C…)
由于变量和输出(函数)的取值只有0和1两种状态,所以我们所讨论的都是二值逻辑函数。
1.逻辑函数的描述方法
常用的逻辑函数描述方法有逻辑真值表,逻辑函数式(简称逻辑式或函数式),逻辑图,波形图,卡诺图和硬件描述语言等。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
(1)逻辑真值表
将输入变量所有的取值下对应的输出值找出来,列成表格,即可得到真值表。
(2)逻辑函数式
将输出与输入之间的逻辑关系写成与,或,非等运算的组合式,即逻辑代数式,就得到了所需的逻辑函数式。
(3)逻辑图
将逻辑函数式中各变量的与,或,非等逻辑关系用图形符号表示出来,就可以画出描述函数关系的逻辑图。
(4)波形图
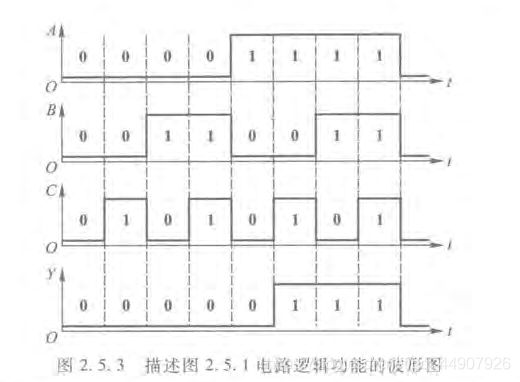
如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列起来,就得到了描述该逻辑函数的波形图。这种波形图也称为时序图。
如果用波形图来描述(1)中的逻辑函数,则只需将表中给出的输入变量与对应的输出变量取值依时间顺序排列起来,就可以得到所要的波形图了!
 +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
各种描述方法间的相互转换
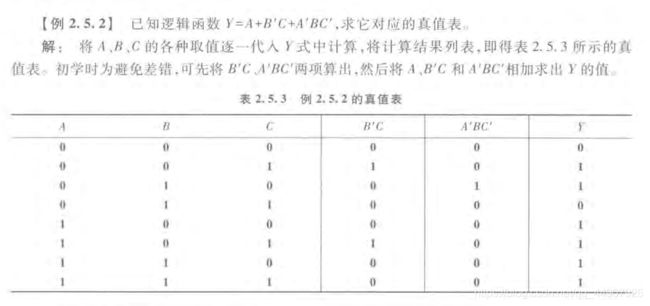
(1)真值表与逻辑函数式的相互转换
真值表转换为逻辑函数式:
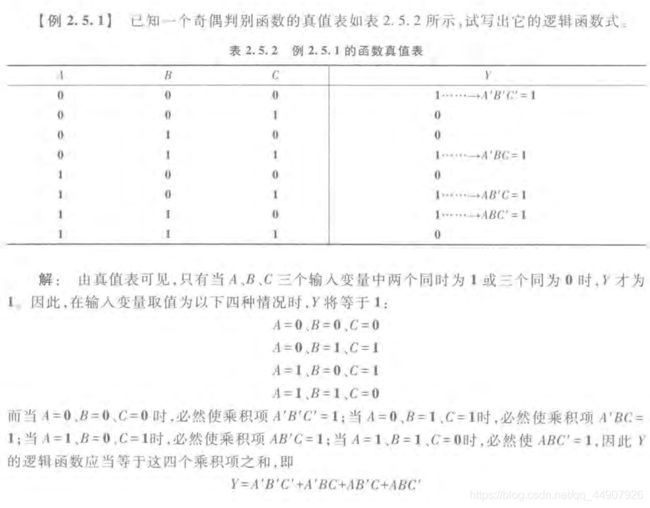 通过上例可总结出由真值表写出逻辑函数式的一般方式,这就是:
通过上例可总结出由真值表写出逻辑函数式的一般方式,这就是:
①找出真值表中使逻辑函数Y=1的那些输入变量取值的组合。
②每组输入变量取值的组合对应一个乘积项,其中取值为1的写入原变量,取值为0的写入反变量。
③将这些乘积项相加,即得Y的逻辑函数式。
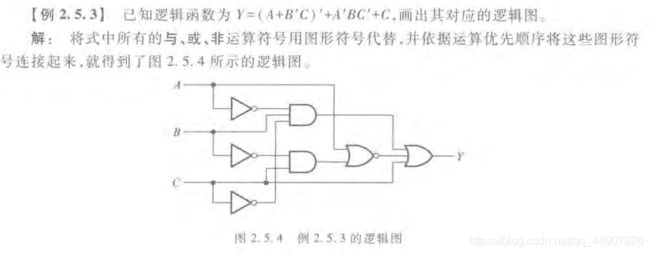
(2)逻辑函数式与逻辑图的相互转换
从给定的逻辑函数式转换为相应的逻辑图时,只要用逻辑图形符号代替逻辑函数式中的逻辑运算符号并按运算优先顺序将它们连接起来,就可以得到所求的逻辑图了。
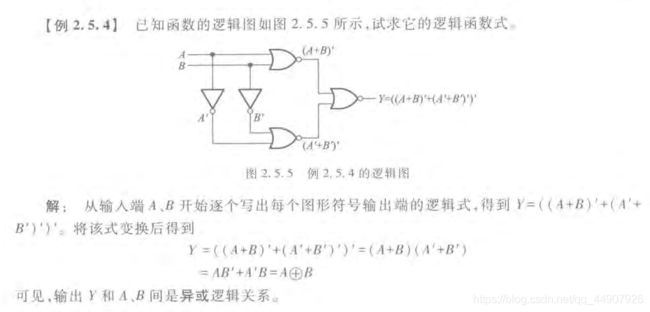
而在从给定的逻辑图转换为对应的逻辑函数式时,只要从逻辑图的输入端到输出端逐级写出每个图形符号的输出逻辑式,就可以在输出端得到所求的逻辑函数式了。
(3)波形图与真值表的相互转换
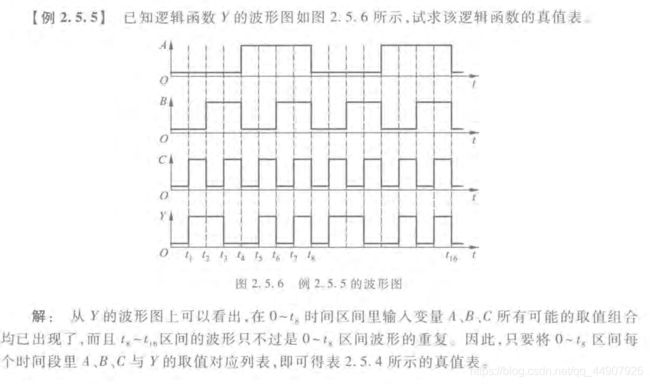
在从已知的逻辑函数波形图求对应的真值表时,首先需要从波形图上找出每个时间段里输入变量与函数输出的取值,然后将这些输入,输出取值对应列表,就得到了所求的真值表。
在将真值表转换为波形图时,只需将真值表中所有的输入变量与对应的输出变量取值依此排列画成以时间为横轴的波形,就得到了所求的波形图。
 +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
(1)逻辑函数的两种标准形式
在讲述逻辑函数的标准形式之前,先介绍一下最小项和最大项的概念,然后再介绍逻辑函数的“最小项之和”及“最大项之积”这两种标准形式。
1.最小项
在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。
例如:A,B,C三个变量的最小项有A’B’C’,A’B’C,A’BC’,A’BC,AB’C’,AB’C,ABC’,ABC共八个(即23个)。n变量的最小项应有2n个。
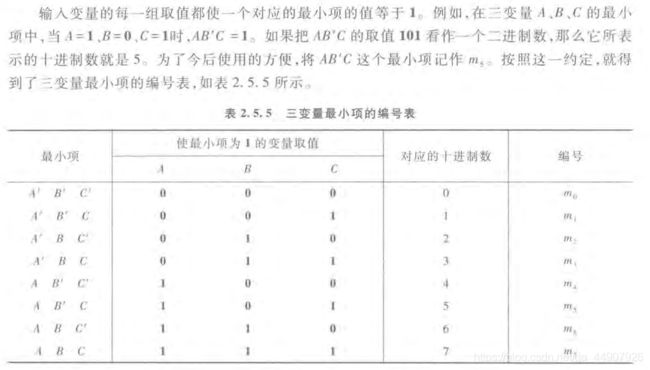 从最小项的定义出发可以证明它具有如下的重要性质:
从最小项的定义出发可以证明它具有如下的重要性质:
①在输入变量的任何取值下必有一个最小项,而且仅有一个最小项的值为1。
②全体最小项之和为1。
③任意两个最小项的乘积为0。
④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
若两个最小项只有一个因子不同,则称这两个最小项具有相邻性。
例如:A’BC’和ABC’两个最小项仅第一个因子不同,所以他们具有相邻性。这两个最小项相加时定能合并成一项并将一对不同的因子消去:
A’BC’ + ABC’ = (A’ + A)BC’ = BC’
2.最大项
在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现一次,则称M为该组变量的最大项。
例如:三变量A,B,C的最大项有(A’+B’+C’),(A’+B’+C),(A’+B+C’),(A’+B+C),(A+B’+C’),(A+B’+C),(A+B+C’),(A+B+C)共八个(即23个)。对于n个变量则有2n个最大项。可知:n变量的最大项数目和最小项数目是相等的。
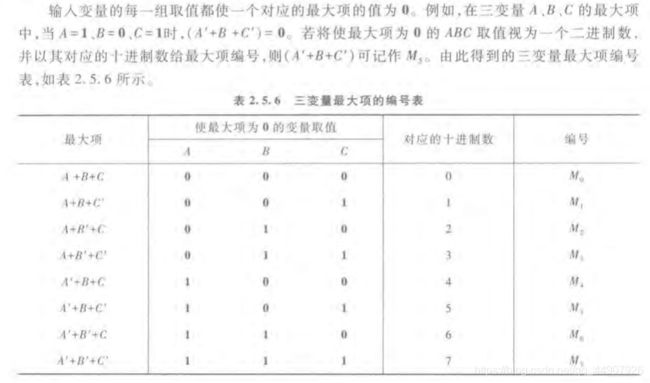
根据最大项的定义同样也可以得到它的主要性质:
①在输入变量的任何取值下必有一个最大项,而且只有一个最大项的值为0。
②全体最大项的乘积为0。
③任意两个最大项之和为1。
④只有一个比那里不同的两个最大项的乘积等于各相同变量之和。
如果将最大项和最小项的两张表对比,可以发现最小项和最大项存在如下关系:
例如:m0 = A’B’C’,则m0’=(A’B’C’)’ = A+B+C =M0
3.逻辑函数的最小项之和形式
首先,将给定的逻辑函数式化为若干乘积项之和的形式,亦称“积之和”形式。然后,再利用基本公式A+A’=1将每个乘积项中缺少的因子补全,这样就可以将与或的形式化为最小项之和的标准形式。
(4)逻辑函数的最大项之积形式
利用逻辑代数的基本公式和定理,首先我们一定能把任何一个逻辑函数式化成若干多项式相乘的或与形式(也称“和之积”形式)。然后再利用基本公式AA’=0将每个多项式中缺少的变量补齐,就可以将函数式的或与形式化成最大项之积的形式了。

2.6逻辑函数的化简方法
函数式中相加的乘积项不能再减少,而且每项中相乘的因子不能再减少时,则函数式为最简形式。
化简逻辑函数的目的就是要消去多余的乘积项和每个乘积项中多余的因子,以得到逻辑函数式的最简形式。常用的化简方法有公式化简法,卡诺图化简法以及适用于编制计算机辅助分析程序的Q-M法等。
1.公式化简法
公式化简法的原理就是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因子,以求得函数式的最简形式。
(1)并项法
利用公式AB+AB’=A可以将两项合并为一项,并消去B和B’这一对因子,而且,根据代入定理可知,A和B均可以是任何复杂的逻辑式。
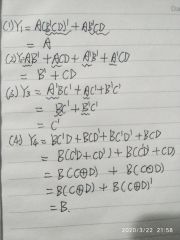
(2)吸收法
利用公式A+AB=A可将AB项消去。A和B同样也可以是任何一个复杂的逻辑式。
(3)消项法
利用公式AB+A’C+BC=AB+A’C及AB+A’C+BCD=AB+A’C将BC或BCD项消去。其中A,B,C,D均可以是任何复杂的逻辑式。
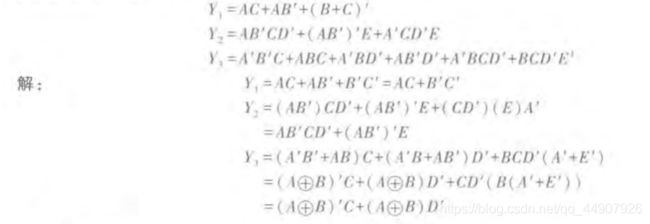
(4)消因子法
利用公式A+A’B=A+B可将A’B中的A’消去。A,B均可以是任何复杂的逻辑式。
(5)配项法
①根据基本公式中的A+A=A可以在逻辑函数式中重复写入某一项,有时能获得更加简单的化简方法。
 ②根据基本公式中的A+A’=1可以在函数式中的某一项上乘以(A+A’),然后拆分为两项分别与其他项合并,有时能得到更加简单的化简结果。
②根据基本公式中的A+A’=1可以在函数式中的某一项上乘以(A+A’),然后拆分为两项分别与其他项合并,有时能得到更加简单的化简结果。
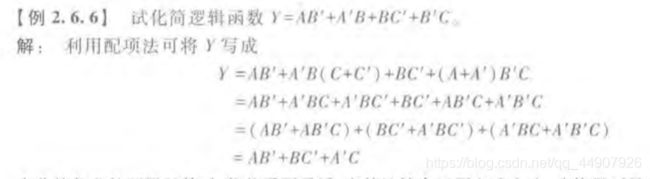 两者合起来综合使用:
两者合起来综合使用:

2.卡诺图化简法
思路:既然对任何逻辑函数都可以展开为最小项之和的形式,那么采用合并最小项的方法化简逻辑函数,就是一种对任何逻辑函数都适用的,而且具有固定操作步骤和方法的化简方法。
卡诺图化简法就是一种基于合并最小项的化简方法!!!
(1)卡诺图介绍:
定义:将n变量的全部最小项各用一个小方块表示,并使具有逻辑相邻性的最小项在几何位置上也相邻地排列起来,所得到的图形称为n变量最小项的卡诺图。
如下图:为二到五变量最小项的卡诺图。图形两侧标注的0和1表示使对应小方格内的最小项为1的变量取值。同时,这些0和1组成的二进制数所对应的十进制数大小也就是对应的最小项的编号。
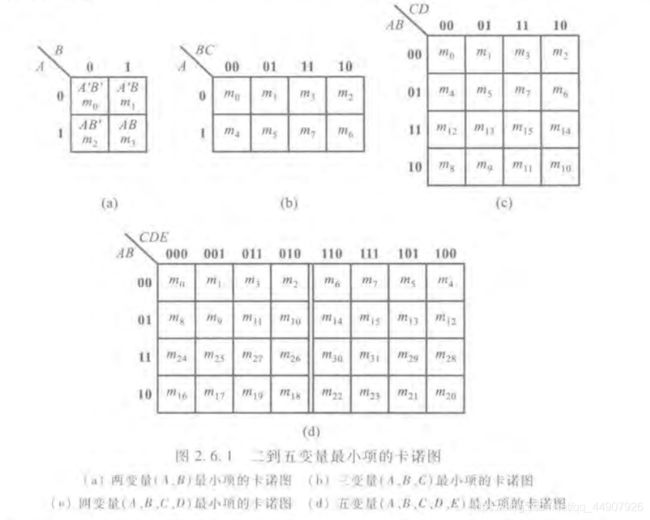
为了保证图中几何位置相邻的最小项在逻辑上也具有相邻性,这些数码不能按自然二进制数从小到大地顺序排列,而必须按照图中的方式排列,以确保相邻的两个最小项仅有一个变量是不同的。
从图中还可以看出,处在任何一行或一列两端的最小项也仅有一个变量不同,所以它们也具有逻辑相邻性。因此,从几何位置上应当将卡诺图看成是上下,左右闭合的图形。
在变量>=5以后,仅用几何图形在两维空间的相邻性来表示逻辑相邻性已经不够了。比如:图中d所示的五变量最小项的卡诺图中,除了几何位置相邻的最小线具有逻辑相邻性以外,以图中双竖线为轴左右对称位置上的两个最小项也具有逻辑相邻性。
既然任何一个逻辑函数都能表示为若干最小项之和的形式,那么自然也就可以设法用卡诺图来表示任意一个逻辑函数。具体的方法是:首先将逻辑函数化为最小项之和的形式,然后在卡诺图上与这些最小项对应的位置上填入1,在其余的位置上填入0,就得到了表示该逻辑函数的卡诺图。也就是说,任何一个逻辑函数都等于它的卡诺图中填入1的那些最小项之和。
(2)用卡诺图化简逻辑函数
利用卡诺图化简逻辑函数的方法称为卡诺图化简法或图形化简法。化简时依据的基本原理就是具有相邻性的最小项可以合并,并消去不同的因子。由于在卡诺图上几何位置相邻与逻辑上的相邻性是一致的,因而从卡诺图上能直观的找出那些具有相邻性的最小项并将其合并化简。
1.合并最小项的原则
若两个最小项相邻,则可合并为一项并消去一对因子。合并后的结果中只剩下公共因子。。
图中(a)和(b)中画出了两个最小项相邻的几种可能情况。例如:图(a)中A’BC(m1)和ABC(m7)相邻,故可合并为;
A’BC+ABC=(A’+A)BC=BC
合并后将A和A’一对因子消掉了,只剩下公共因子B和C。
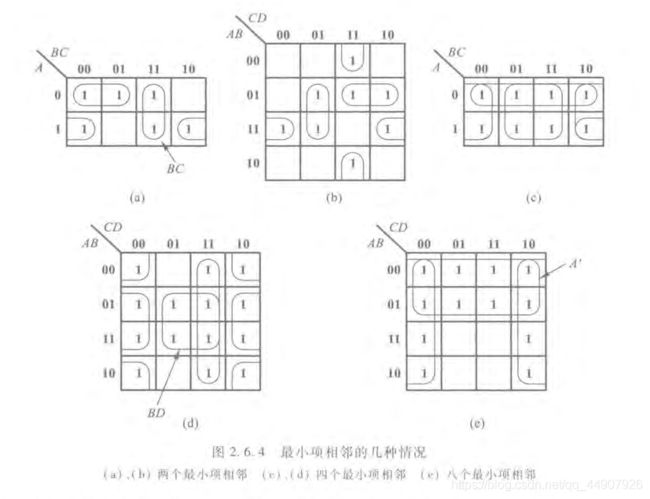 若四个最小项相邻并排列成一个矩形组,则可合并为一项并消去两对因子。合并后的结果中只包含公共因子。
若四个最小项相邻并排列成一个矩形组,则可合并为一项并消去两对因子。合并后的结果中只包含公共因子。
例如:图(d)中,A’BC’D(m5),A’BCD(m7),ABC’D(m13)和ABCD(m15)相邻,故可合并。合并后得到:
A’BC’D+A’BCD+ABC’D+ABCD
=A’BD(C+C’)+ABD(C+C’)
=BD(A+A’)=BD
可见,合并后消去了A,A’和C,C’两对因子,只剩下四个最小项的公共因子B和D。
总结:
合并最小项的一般规则:如果有2**n个最小项相邻(n=1,2,…)并排列成一个矩形组,则它们可以合并为一项,并消去n个因子。合并后的结果中仅包含这些最小项的公共因子。
2.卡诺图化简法的步骤:
(1)将函数化为最小项之和的形式
(2)画出表示该逻辑函数的卡诺图
(3)找出可以合并的最小项
(4)选取化简后的乘积项。选取的原则:
①这些乘积项应包含函数式中所有的最小项(应覆盖卡诺图中所有的1)
②所用的乘积项数目最少。也就是可合并的最小项组成的矩形组数目最少。
③每个乘积项包含的因子最少。也就是每个可合并的最小项矩形组中应包含尽量多的最小项。
3.具有无关项的逻辑函数及其化简
(1)约束项,任意项和逻辑函数式中的无关项
约束项:
第一种特殊情况输入变量的取值不是任意的,对输入变量取值的限制称为约束。我们把具有这种特点的逻辑函数称为具有约束的逻辑函数,同时把这一组输入变量称为具有约束的一组逻辑变量。
任意项:
第二种特殊情况是在输入变量的某些取值下函数值是1还是0皆可,并不影响电路的功能。在这些变量取值下,其值等于1的那些最小项称为任意项。存在任意项的逻辑函数也叫做不完全定义的逻辑函数。
注意:因为使约束项的取值等于1的输入变量取值是不允许出现的,所以约束项的值始终为0,;
而任意项则不同,在函数的运行过程中,有可能出现使任意项取值为1的输入变量取值。
逻辑函数式中的无关项:
我们将约束项和任意项统称为逻辑函数式中的无关项。这里所说的“无关”是指是否把这些最小项写入逻辑函数式无关紧要,可以写入也可以删除。

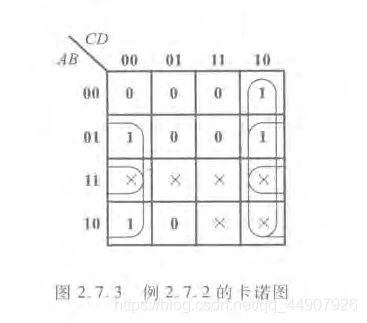
(2)无关项在化简逻辑函数式中的应用
注意:1.加入的无关项应与函数式中尽可能多的最小项(包括原有的最小项和已写入的无关项)具有逻辑相邻性。
2.合并最小项时,究竟把卡诺图中的无关项作为1(即认为函数式中包含了这个最小项)还是作为0(即认为函数式中不包含这个最小项)对待,应以得到的相邻最小项矩形组合最大,而且矩形组合数目最少为原则。
 通过画卡诺图解决这一问题:::
通过画卡诺图解决这一问题:::