tong'g###Cholesky分解
概念
Cholesky分解是指将一个正定埃尔米特矩阵分解成唯一一个下三角矩阵与其共轭转置之乘积。
正定 :当且仅当对于所有的非零实系数向量z,都有,M为正定矩阵。(半正定是)
- 所有特征值均为正;
- 所有顺序主子阵的行列式均为正;
- 存在唯一的下三角矩阵(其主对角线上的元素全是正的)满足:。
埃尔米特矩阵:每一个第i行第j列的元素都与第j行第i列的元素的复共轭。对于实矩阵,就是对称矩阵。
应用
Cholesky分解主要被用于求解Ax=b。。如果A是对称正定的,我们可以先求出A=LL',随后通过后向替代法 Ly=b求得y,再通过前向替代法L'x=y求得x。实际应用中,Cholesky分解及其LDL变形在求解线性方程组中的效率约两倍于LU分解。
代码及思路
主要通过公式1和公式2不断迭代求出每行的参数。
- 公式1求得对角参数;
- 公式2通过更新后的同列参数和对角参数求出。
公式:
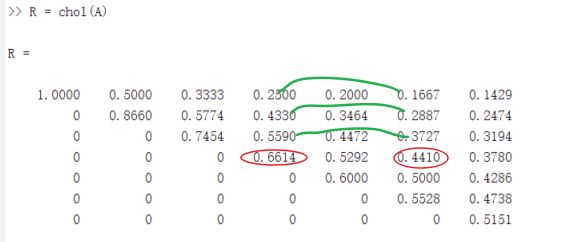
图片示意:
代码:
# include
# include
# include
# include
//定义矩阵和相量
typedef float f32_mat_t[7][7]; /**< a matrix */
typedef float f32_vec_t[7]; /**< a vector */
//Cholesky分解
bool chol_factor(const f32_mat_t* f_A, f32_mat_t* f_L, int n)
{
bool b_retVal = 1;
int i, j, k;
float sum;
const float *pA;
float *pL;
float *pL1;
float *pL2;
float fLii;
/** @llr - This function shall provide a lower triangular matrices for a given symmetric positive definite matrix using Cholesky decomposition.*/
/* Copying lower triangular matrix of f_A into f_L and fill the rest with 0 */
//相当于线性方程组迭代消元法
for (i = 0u; i < n; i++)
{
pL = &(*f_L)[i][0];
pA = &(*f_A)[i][0];
for (j = 0u; j <= i; j++)
{
(*pL) = (*pA);
pL++;
pA++;
}
for (j = i + 1u; j < n; j++)
{
(*pL) = 0.0f;
pL++;
}
}
for (i = 0u; i < n; i++)
{
fLii = (*f_L)[i][i];
for (j = i; j < n; j++)
{
sum = (*f_L)[j][i];
pL1 = &(*f_L)[i][0];
pL2 = &(*f_L)[j][0];
for (k = 0u; k < i; k++)
{
sum -= (*pL1) * (*pL2);
pL1++;
pL2++;
}
if (i == j)
{
if (sum <= 0.0f)
{
b_retVal = 0;
}
else
{
fLii = sqrt(sum);
(*f_L)[i][i] = fLii;
}
}
else
{
(*f_L)[j][i] = sum / fLii;
}
}
}
return b_retVal;
}/** @enddetails */
int main(void)
{
f32_mat_t B = { { 1, 0.500000000000000, 0.333333333333333, 0.250000000000000, 0.200000000000000, 0.166666666666667, 0.142857142857143 },
{ 0.500000000000000, 1, 0.666666666666667, 0.500000000000000, 0.400000000000000, 0.333333333333333, 0.285714285714286 },
{ 0.333333333333333, 0.666666666666667, 1, 0.750000000000000, 0.600000000000000, 0.500000000000000, 0.428571428571429 },
{ 0.250000000000000, 0.500000000000000, 0.750000000000000, 1, 0.800000000000000, 0.666666666666667, 0.571428571428571 },
{ 0.200000000000000, 0.400000000000000, 0.600000000000000, 0.800000000000000, 1, 0.833333333333333, 0.714285714285714 },
{ 0.166666666666667, 0.333333333333333, 0.500000000000000, 0.666666666666667, 0.833333333333333, 1, 0.857142857142857 },
{ 0.142857142857143, 0.285714285714286, 0.428571428571429, 0.571428571428571, 0.714285714285714, 0.857142857142857, 1 } };
const f32_mat_t *A = &B;
f32_mat_t C;
memset(C, 0, sizeof(f32_mat_t));
f32_mat_t *L;
bool ok;
L = &C;
ok = chol_factor(A, L, 7);
for (int i = 0;i < 7;i++) {
for (int j = 0;j < 7;j++)
printf("%f ", (*L)[i][j]);
printf("\n");
}
getchar();
return 0;
}
求线性方程组Ax=b
/**
* @brief Solve the f_L*fL'*f_x = f_b and save the result in f_x
*
* @param[in] f_L: matrix n*n
* @param[in] f_b: vector
* @param[in] n: size
*
* @param[out] f_x: vector to solve
*
* @return b_retVal: True
*
* @funcdetails
*/
bool_t chol_subtitute(const f32_mat_t* f_L, const f32_vec_t* f_b, f32_vec_t* f_x, u16_t n)
{
bool_t b_retVal = TRUE; /* Later may add some checks for b_retVal in this function */
u16_t i, j;
f32_t f_sum;
f32_t *pX;
f32_t *pXi;
f32_t *pXj;
const f32_t *pL;
const f32_t *pB;
f32_t fLii;
/** @llr - This function shall solve the unknown vector f_x given a matrix f_L and a vector f_b with the relation f_L*fL'*f_x = f_b.*/
pX = &(*f_x)[0];
pB = &(*f_b)[0];
/* Copy f_b into f_x */
for (i = 0u; i < n; i++)
{
(*pX) = (*pB);
pX++;
pB++;
}
/* Solve Ly = b for y */
pXj = &(*f_x)[0];
for (i = 0u; i < n; i++)
{
f_sum = (*f_x)[i];
fLii = (*f_L)[i][i];
pXi = &(*f_x)[0];
pL = &(*f_L)[i][0];
for (j = 0u; j < i; j++)
{
f_sum -= (*pL) * (*pXi);
pL++;
pXi++;
}
(*pXj) = f_sum / fLii;
pXj++;
}
/* Solve L'x = y for x */
for (i = 1u; i <= n; i++)
{
f_sum = (*f_x)[n - i];
pXj = &(*f_x)[n - i + 1u];
pL = &(*f_L)[n - i + 1u][n - i];
for (j = n - i + 1u; j < n; j++)
{
f_sum -= (*pL) * (*pXj);
pXj++;
pL += MATRIX_DIMENSION; /* PRQA S 0488 */
}
(*f_x)[n - i] = f_sum / (*f_L)[n - i][n - i];
}
return b_retVal;
}/** @enddetails */
求矩阵的逆
/**
* @brief Calculate the inverse of a matrix which should be symetric positive definite.
*
* @param[in] f_A: matrix n*n
* @param[in] n: size of matrix
*
* @param[out] f_invA: inverse matrix
*
* @return b_retVal: true if successful otherwise
*
* @funcdetails A=LL' LL'*Ainv=I LU=I L'*Ainv=U
*/
bool_t InvChol(const f32_mat_t* f_A, f32_mat_t* f_invA, u16_t n)
{
bool_t b_retVal;
f32_mat_t f_L;
f32_vec_t f_b, f_x;
u16_t i, j;
/** @llr - The function shall calculate the inverse matrix for a given symmetric positive definite matrix.*/
/* A = f_L*f_L' */
b_retVal = chol_factor(f_A, &f_L, n);
if (b_retVal == TRUE)
{
for (i = 0u; i < n; i++)
{
f_b[i] = 0.0f;
}
for (i = 0u; i < n; i++)
{
if (i != 0u)
{
f_b[i-1u] = 0.0f;
}
else
{
/* Do nothing */
}
f_b[i] = 1.0f;
b_retVal &= chol_subtitute((const f32_mat_t*)&f_L, (const f32_vec_t*)&f_b, &f_x, n);
for (j = 0u; j < n; j++)
{
(*f_invA)[j][i] = f_x[j];
}
}
}
else
{
/* Do nothing */
}
return b_retVal;
}/** @enddetails */