解决回溯问题,实际上就是一个决策树的遍历过程。
你只需要思考 3 个问题:
1. 路径:也就是已经做出的选择;
2. 选择列表:也就是你当前可以做的选择;
3. 结束条件:也就是到达决策树底层,无法再做选择的条件。
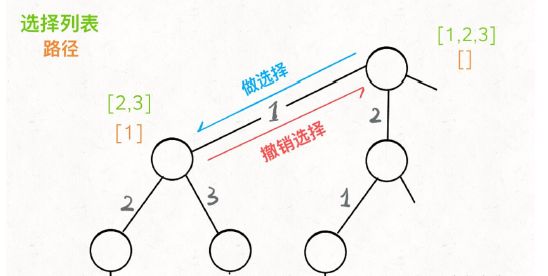
其核心就是 for 循环里的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
一、全排列问题
我们在高中的时候就做过排列组合的数学题,我们知道 n 个不重复的数,全排列共有 n! 个。
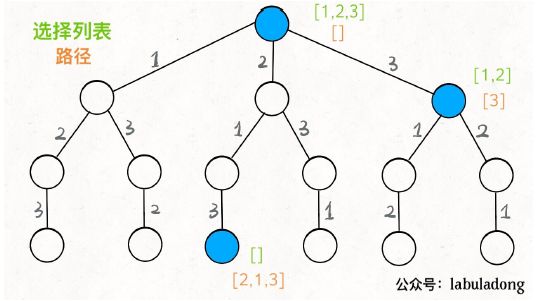
比如 1,2,3,它们的全排列共有 6 种,在我们不知道 n! 这个公式前,是通过枚举来计算的:第一个数选1,第二个数选2,第三个数选3——这是第一种;然后退回来,第二个数选3,第三个数选2——这是第二种……
其实这就是回溯算法。这棵决策树的所有全路径就是全排列。这棵树的每个节点分枝时,都在做决策——这里选1,选2,还是选3。(注意全排列问题有制约条件,路径之前已经排过的数字后面不能再排)
在这个问题种,已经选过的节点,就是「路径」,当前分支可选项就是「选择列表」,当可选列表为空时,就到了树的底层,称为「结束条件」。
我们定义的backtrack 函数就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
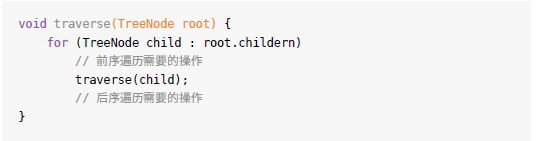
再进一步,如何遍历一棵树?多叉树的遍历框架:
因为做选择会改变状态,所以回溯算法在选择完一个分支,走完当前分支所有子树后,回到父节点时撤销掉上次选择分支对状态的影响,这样就可以利用前面已经做过的所有父选择,达到全排的目的。
值得注意的是,不管怎么优化,回溯问题都符合回溯框架,时间复杂度不可能低于O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
二、N皇后问题
N皇后问题非常经典,常见八皇后问题。
N * N 的棋盘,放置 N 个皇后,使它们不能相互攻击。【皇后攻击范围为同行、同列、同斜线(↖↙↗↘)】
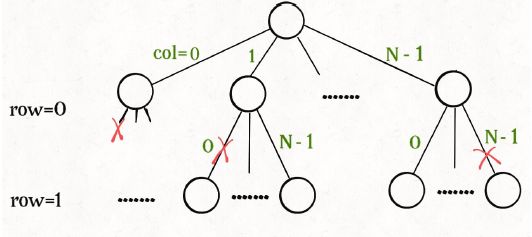
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的一行;每个节点可以做出的选择是,在改行的任意一列放置一个皇后。
直接套用框架:
这部分主要代码跟全排列问题差不多,isValisd函数的实现也很简单:
可以传入n=8进行验证,八皇后问题的答案是92。
函数backtrack依然像个在决策树上游走的指针,通过 row 和 col 就可以表示函数遍历到的位置,通过 isValid 函数可以将不符合条件的情况剪枝:
虽然有 valid 函数剪枝,但是最坏时间复杂度仍然是O(N^(N+1)),而且无法优化。如果 N = 10 的时候,计算就已经很耗时了。
三、总结
回溯算法就是个多叉树的遍历问题,关键就是再前序遍历和后续遍历的位置做的一些操作:算法框架如下:
实际上,回溯算法和动态规划也蛮像的,只不过,动态规划的高层节点依赖于低层节点的选择结果,并且伴随求极值问题;而回溯算法高层节点代表已经做出的选择,低层节点表示新的选择,直到到达叶节点表示完成一条选择通路,同时记录下符合条件的通路,最后返回所有可能的解。
动态规划的三个需要明确的点就是「状态」「选择」和「base case」,对应到回溯算法就是走过的「路径」「选择列表」和「结束条件」。
某种程度上说,动态规划的暴力求解阶段就是回溯算法。只是有的问题据有重叠子问题性质,可以用dp table 或 备忘录优化,将递归树大幅剪枝,这就编程了动态规划。而如上的两个问题,都没有重叠子问题,也就是回溯算法问题,复杂度非常高是不可避免的。