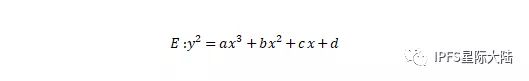【纯干货】量子计算机真的能摧毁区块链网络吗？

作者：Neo Ge

校验：Junkai Zeng

最近有很多朋友问到我关于量子计算机的问题，其中最大的隐忧是担心量子计算会凭借超强算力，使得加密货币不再加密，甚至摧毁区块链网络。先说答案：不会。不过要想明白这一点，就要了解什么是量子计算和区块链的密码算法。

本文特别鸣谢Junkai Zeng提供的技术支持，他不仅是我的老同学，同时还是弗吉尼亚理工物理学博士，研究方向便是量子计算，目前在LA一家红杉投资的量子公司就职。

量子计算

要想明白量子计算，我们就要了解什么是经典计算。我们要知道经典计算机发展道路上遇到的一个瓶颈叫做摩尔定律Moore’s Law，即集成电路上可容纳的晶体管数量，每隔两年便会增加一倍。

这就导致晶体管的体积越来越小，当它小到约2nm的时候，由于2nm级别上的晶体管只能容纳10个原子，电子的行为将不再服从传统的半导体理论，而是遵循量子力学。而随着晶体管集成度的提高，芯片产生的热量也会越来越高。

这些负面的影响都严重阻碍了经典计算机的发展。在这种担忧之下，人们想出了诸如光子计算机、生物计算机、量子计算机等解决方法。

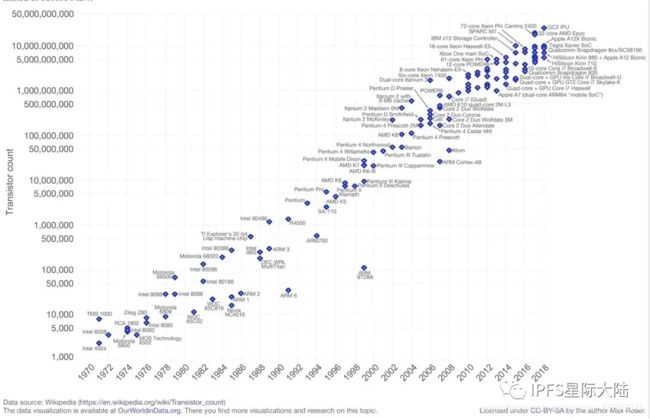摩尔定律 - 集成电路芯片上晶体管的数量 (1971-2018)

人们为什么这么看重量子计算机？

首先，我们要知道经典计算机的运算是通过逻辑电路来完成的，二进制的1和0在计算机中代表逻辑运算，又叫布尔代数。

1代表真（高电平），0代表假（低电平）。

最常见的逻辑运算是与、或、非这三种。举个例子，真与真结果是真，真与假结果是假；非真即假，非假即真。这些运算都是通过一个个逻辑门来完成的，其中这些逻辑门有可逆的也有不可逆的。比如非门输入一个1（比特真），输出为一个0（比特假），所以非门就是可逆门，因为我们可以通过输出0（比特假）倒推出输入1（比特真）。但如果一个与门的输出是0（比特假），那么输入的比特有三种可能，分别是00、01、10，我们无法明确的一对一映射回输入，所以与门就是不可逆门。本来两个比特的信息通过与门之后变为一个比特的信息，这里丢掉了一个比特的信息。

Landauer原理

Rolf Landauer

1961年，IBM工程师Rolf Landauer发现每擦除一个比特的信息需要热力学成本，即产生至少kTln2的热量，而写入信息则不需要热力学成本。其中，k是玻尔兹曼常数，T是环境温度。这就是大名鼎鼎的Landauer原理，通过这个原理我们知道信息同样具备物理性质。而经典计算机中基本上都是不可逆操作，所以经典计算机会产生越来越多的热量。

这是Landauer在思考麦克斯韦妖的问题上得出来的结论：因为处理信息是要付出代价的，而小妖的记忆不可能是无限的，它总会删除一些记忆导致熵增，所以小妖不能存在。

于是人们就想如果将经典计算机中的不可逆操作转换成可逆操作，那问题不就解决了嘛。理论上，一个称为幺正变换的操作 – 对量子态的一种处理手段，放在经典计算机上刚好能解决散热的问题。然而，经典计算机虽然擅长微分方程类问题，即模拟经典物理系统。但如果仍用微分方程来描述量子物理系统，经典计算机难以担此重任。所以后来费曼等物理学家提出直接将经典比特转换成量子比特，直接使用量子来模拟量子系统。（我们在文章开头视频中听到的就是理查德·费曼的声音）

量子的天然优势 – 并行计算

在经典计算机中，我们使用二进制来提高计算效率。假如你想让经典计算机计算100+100，首先要将十进制的100转换成二进制的1100100。在经典计算机中，需要使用7个不同状态的晶体管来表示二进制的1100100。通俗来讲，一个晶体管就是一个比特位，且只能表示1或0（高电平或低电平）。量子计算机不同，一个量子的双态系统就是一个比特位，叫量子比特qubit。

双态系统就像是电子的自旋、光子的偏振，最通俗的解释是薛定谔的猫。薛定谔的猫在没有进行观测的时候，从量子力学角度来看，它既死又活，处于死和活的叠加态，这种状态遵循的是量子的态叠加原理。假如我们把经典计算机中的晶体管换成薛定谔的猫，一个薛定谔的猫可以同时代表1和0，而不是经典计算机中的1或0了。两个薛定谔的猫可以表示00、01、10、11四种状态，而经典计算机中两个比特位只能取这4种状态之一。

那么对于n个比特位，经典比特只能表示1个数，而量子比特在理论上可以同时表示2^{n次方个数，这就是经典计算机和量子计算机的最大区别。2}n这种呈指数增长的碾压式诱惑使得人们对于量子计算机有了这么大的兴趣 – 也就是天然并行计算的好处。

薛定谔的猫

如何实现量子计算机

难点1：拿什么来做量子比特？

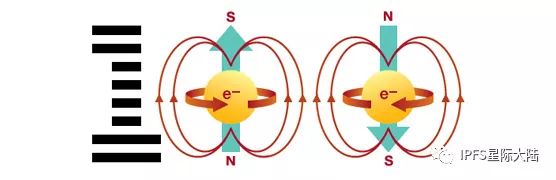
从物理学家的角度来说，理论上两能级量子体系都可以作为量子比特。比如电子的自旋在没有进行测量的时候处于既上又下的叠加态，一旦测量就会出现要么朝上要么朝下的本征态。

电子的自旋

难点2：量子计算机的算法？

由于算法是计算机的灵魂，而经典算法只适用于经典比特，就算做好量子芯片，经典算法也不能在量子芯片上使用。1994年贝尔实验室的彼得·秀尔发表了可以进行大数质因数分解的秀尔算法。

彼得·秀尔

质因数分解问题是一个NP问题，也就是在经典算法中它的复杂度不能够在多项式时间内完成。一般的算法进行质因数分解复杂度是O即e^n，n指这个数用二进制表示的位数。目前使用最快的经典超算进行一个300位数（十进制）的质因数分解，需要花费约15万年的时间。这也是为什么大数的质因数分解可以用来进行加密的原因，因为几乎没有可能通过经典计算机暴力算出哪两个质数相乘来解密。

但秀尔算法可以将复杂度降到 (logN)^3，也就是说秀尔算法将一个NP问题变成了P类问题。使用秀尔算法同样进行300位数的质因数分解，理论上需要不到1分钟的时间。

除此之外，秀尔还解决了一个困扰物理学家十几年的问题，假如用秀尔算法使用量子比特进行计算，结果仍是一堆量子比特，我们需要对结果进行测量。然而薛定谔的猫告诉我们，测量猫死活的概率各占50%，所以理论上测得的结果还是随机的。

秀尔告诉我们，通过使用秀尔算法，需要的数据会相干相长，不需要的数据相干相消。最后的测量正确结果的概率是1。由于如今银行乃至政府的保密资料都是基于质数的RSA算法进行加密的，所以自从1994年秀尔算法公布后，量子计算就引发了世界各国政府的强烈兴趣。就连美国国防高级研究计划局DARPA也加入了这场争夺（DARPA曾经提出并投资了互联网、Unix系统和全球定位系统GPS等）。

2001年IBM的华裔研究员艾萨克·庄他们的研究团队，通过核磁共振进行了秀尔算法演示，即5个氟原子和两个碳原子组成的一个分子，用每个原子的核自旋来做量子比特，7个qubit相当于2^7也就是128个经典比特。用这台迷你量子计算机使用秀尔算法进行了15的质因数分解，给出的结果是3和5，成功证明了秀尔算法是可行的。后来证明，秀尔算法也可以用于离散对数问题上的求解。量子计算机的算法，除了秀尔算法还有Grover、QAOA、VQE算法等，后面我们还会再次提到Grover算法。

难点3：如何保持量子的相干性？

量子的相干性很难保持，就算不对处于叠加态的量子进行测量，它也会和周围的环境发生量子纠缠然后变成确定的状态，即变成经典的，也就是俗称的波函数坍缩，这个过程叫做量子退相干。为了抵抗量子退相干带来的影响，我们主要有两种方法：

量子纠缠

量子纠错；和经典计算机类似，以牺牲资源为代价，比如使用8个量子比特位当1个用，有一两个退相干没关系，将少数退相干的量子纠正过来。使用纠错码存在两个问题：一个是量子计算每一步的操作必须低于某个比例，这样错误才可以被纠正，比如错误率低于1%；另一个是纠错码需要用大量物理层面的量子比特来编码一个逻辑层面的量子比特，这些都给在硬件层面实现量子计算带来了极大的障碍。

更好的技术操控量子系统：因为量子力学的一些性质，即使是实现同样的操作，物理层面上用不同的方式去控制量子比特也将会带来截然不同的保真度。通过使用更好的方式去优化这些操作，可以将错误率控制在量子纠错的阈值之下，为实现更通用的量子纠错铺路。

至此，量子计算机在理论上就不存在什么难题了。至于物理层面，量子芯片怎么做、用什么做。这就是目前各大机构的主要研究方向，要保证量子比特在保持相干性的同时做到集成化。典型实现量子比特的硬件实现方案，主要包括光学系统、半导体量子点、超导电路、冷原子、离子井等等。谷歌、IBM和阿里达摩院等业界研究机构致力于的便是通过超导电路实现量子芯片。

今年9月，谷歌公司宣布成功使用包含53个有效量子比特的处理器实现了“量子霸权”（Quantum Supremacy）。需要指出的是，“量子霸权”指的是实现了在某些问题上面量子计算可以做到用经典计算机无法做到的事情，实现了“量子”对“经典”的霸权，也就是一个新技术对旧技术的霸权，而非某个企业或者研究机构在国际上领先，从对其他企业和研究机构产生了霸权。

区块链的加密算法

这里，我们以比特币为例子向大家介绍区块链的加密算法。比特币的加密算法有两类三种，分别是椭圆曲线算法、SHA256哈希算法和RIPEMD160哈希算法。大致流程如下：

私钥 -> 椭圆曲线算法 -> 公钥 -> SHA256 -> RIPEMD -> SHA256 -> SHA256 -> 地址

其中单向箭头意味着经典计算中算法不可逆推，从地址逆推不了公钥，公钥逆推不了私钥。由于量子计算就是将经典计算中的不可逆变为可逆，为了方便阐述，我们从地址开始向回逆推。

哈希算法

比特币运用的两种哈希算法中，SHA256是SHA-2下细分出的一种算法，它是一种密码散列函数算法标准，由美国国家安全局研发；RIPEMD (RIPE Message Digest) 也是一种哈希函数。对于对称加密与哈希函数，存在量子攻击，但危险性较小。Grover算法只能将经典计算下2^{256的难度降低到依然是天文数字的2}128，而从公钥到地址需要进行1次RIPEMD和3次SHA256哈希运算，所以在针对对称加密颠覆性量子算法诞生之前，我们不必过多担心。

由于比特币挖矿采用的是SHA256算法，今后如果有一种远优于Grover算法的量子算法诞生，且随着时间的推移，量子计算机的速度越来越快、价格越来越低，那么量子计算机的确会在比特币挖矿方面超越经典计算机。但这个进程就像是从CPU挖矿到GPU挖矿再到ASIC挖矿一样，我们完全不必担心。

椭圆曲线算法

从公钥逆推回私钥的壁垒只有一个—椭圆曲线密码学（Elliptic curve cryptography），简称ECC，这是一种建立公开秘钥加密的算法，也就是非对称加密。从数学角度来看，椭圆曲线可以这样表示：

比特币基于secp256k1曲线的椭圆曲线数字签名算法（ECDSA）便是椭圆曲线其中的一种。由于椭圆曲线算法依赖于离散对数困难问题，而上文提到的秀尔算法又可以被用为离散对数的求解，所以理论上拥有一定有效量子比特的量子计算机会对比特币的椭圆曲线算法造成威胁。

然而secp256k1曲线的安全性是2^128 ，所以就算秀尔算法将其复杂度降低到 128^3，理论上攻击secp256k1曲线的量子计算机也至少要有1500个逻辑量子比特。考虑到要使用量子纠错，实际上需要的物理量子比特将远远高于这个数字。

今年9月份谷歌宣布的迄今为止最大的通用量子计算机也只有53个物理量子比特，错误率极高不说，并且只能在接近绝对零度的实验室条件下运行。与此同时，谷歌使用的超导芯片在扩展性上天然存在很多问题，所以如何在保持可以操控的基础上增加更多的量子比特在可预见的将来都将是一个非常大的挑战。虽然不能完全预测量子计算将以何种速度发展，但预计比特币的256位ECDSA密钥至少在2040年之前是安全的。

比特币本身已经具有一些内置的抗量子特质，如果你有一个好的比特币使用习惯，即一个钱包地址只使用一次，那么你的公钥只有当你花费比特币时才会被广播到全网。这时，量子计算机将只有极短的时间来破解你的私钥，即从交易发送到交易信息被添加到区块中的这段时间。

让我们假设你并没有一个好的比特币使用习惯，量子计算机发展也突飞猛进，所有常用的公钥算法都被破坏了。比特币还有一个杀手锏，那就是升级它的加密算法。众所周知，如果技术手段能够破解一种密码，它就必然可以再制造出一种破解不了的密码。当前，在针对量子安全的公钥加密算法之中，比特币专家倾向于偏爱基于Lamport签名的加密系统。虽然Lamport签名的计算速度非常快，但也主要有两个缺点：

签名会非常大，至少数个kB（比现在大40-170倍），这对比特币的整体可扩展性将是非常不利的。

在创建每个秘钥对时，你需要设置可使用此秘钥签名的有效最大数量。若签名超过此数目将变得不再安全。但如果你每个地址只是用一次，这并不是一个大问题。

除此之外，在密码学家对后量子密码学的研究中，超奇异椭圆曲线同源密钥交换（SIDH）也有望取代当前的常规椭圆曲线密钥交换（ECDH）。基于高维度向量空间的密码学，即格密码学也会将破译难度再提升一个宇宙量级，足以对抗量子计算。新的公钥算法将作为软分叉添加到比特币，比特币用户只需将其比特币发送到新创建的地址即可实现量子安全。

密码学与计算机科学

我们研究量子计算机对于区块链的挑战时，很难不去反复思考密码学与计算机科学的关系。历史的事实总是惊人的纠缠相似，破译密码，本是计算机诞生的源动力。

第二次世界大战期间，计算机科学与人工智能之父 – 艾伦·图灵受雇于英国皇家海军从事对德国机密军事密码的破译工作。当时的纳粹军方拥有一套复杂而精密的通讯安全系统 – Enigma密码机。它由一系列不断随机变化的转子组成，其复杂性高达1京即1亿亿，以当时的破译手段极难攻克。图灵利用他设计的破译机bombe先是破译了Enigma，接着破译了Tunny密码在内的当时纳粹军方使用的几乎所有等级的通信加密系统。这使得盟军对德国的军事指挥和计划了如指掌，硬生生帮助盟军提前至少两年战胜了纳粹德军，结束了第二次世界大战。

艾伦·图灵

图灵提出一种将人的计算行为抽象掉的数学逻辑机，即图灵机。后来现代计算机之父冯诺依曼运用冯诺依曼结构完成了图灵机的实现。以他名字命名的图灵测试，作为一种用于判定机器是否具有智能的测试方法被广泛使用。图灵在数学和逻辑方面的辉煌成就也为计算机和整个数字时代的发展制定了宏伟的蓝图。为了表彰他的开创性贡献，以其名字命名的计算机界的诺贝尔奖 – 图灵奖作为该领域最高的奖项于1966年被正式成立。

对于即将到来的量子时代，作为区块链从业者的我们应该怀着敬畏与期待的心情，迎接它的到来。量子计算机的价值在于解决典型的NPC问题和其他如三体、七桥、蛋白质折叠、地震预测、天气预报等问题。量子计算机不是万能的，它并不能取代经典计算机。

参考资料

[1] Martin Roetteler, Michael Naehrig, Krysta M. Svore, and Kristin Lauter. “Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms” Microsoft Research, USA (2017): 1706.06752

[2] Matthew Amy, Olivia Di Matteo, Vlad Gheorghiu, Michele Mosca, Alex Parent, and John Schanck. “Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3” Quantum Physics (2016): 1603.09383

[3] 孙昌璞, 全海涛. “麦克斯韦妖与信息处理的物理极限” 物理·42卷11期 (2013): 10.7693

[4] Craig Gentry. “Fully Homomorphic Encryption Using Ideal Lattices” Stanford University and IBM Watson (2009): cs.cmu.edu

[5] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C. Bardin, Rami Barends et al. “Quantum supremacy using a programmable superconducting processor” Nature 574, no. 7779 (2019): 505-510

[6] I. Stewart, D. Ilie, A. Zamyatin, S.Werner, M. F. Torshizi and W. J. Knottenbelt. “Committing to quantum resistance: a slow defence for Bitcoin against a fast quantum computing attack” Royal Society Open Science 5, no. 6 (2018): 180410

[7] Divesh Aggarwal, Gavin K. Brennen, Troy Lee, Miklos Santha, and Marco Tomamichel. “Quantum attacks on Bitcoin, and how to protect against them” Quantum Physics (2017): 1710.10377

[8] Zhe Zhou. “MommyTalk” YouTube (2019): https://youtu.be/OHTqCYCQJe0