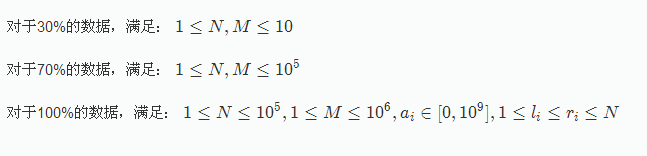由希儿
由希儿

考前的板子硬邦邦

最长公共子序列

  • 题目描述

给出1-n的两个排列P1和P2，求它们的最长公共子序列。

  • 输入输出格式

输入格式：

第一行是一个数n，
接下来两行，每行为n个数，为自然数1-n的一个排列。

输出格式：

一个数，即最长公共子序列的长度

  • 输入输出样例

输入样例#1：

5
3 2 1 4 5
1 2 3 4 5

输出样例#1：

3

说明

【数据规模】
对于50%的数据，n≤1000
对于100%的数据，n≤100000

转化成最长上升子序列然后 nlogn 解决。

#include 
#include 
#include 
#include 
#define MAXN 1000005
#define INF 233333333
using namespace std;
int n,a[MAXN],b[MAXN],f[MAXN],cnt;
int main() {
    scanf("%d",&n);
    for(int i=1,gg;i<=n;i++) {
        scanf("%d",&gg);
        a[gg]=i;
    }
    for(int i=1,gg;i<=n;i++) {
        scanf("%d",&gg);
        if(a[gg]>0) b[cnt++]=a[gg];
    }
    fill(f,f+n,INF);
    for(int i=0;i

最小（最大）生成树

  • 题目描述

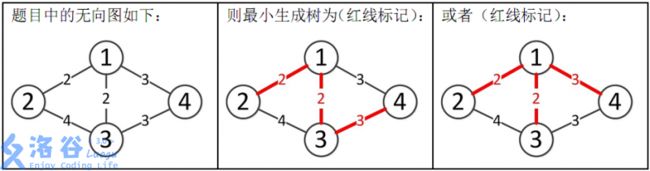
如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

  • 输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）
接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

  • 输入输出样例

输入样例#1：

1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例#1：

7

  • 说明

时空限制：1000ms,128M
数据规模：
对于20%的数据：N<=5，M<=20
对于40%的数据：N<=50，M<=2500
对于70%的数据：N<=500，M<=10000
对于100%的数据：N<=5000，M<=200000
样例解释：


考前的板子硬邦邦_第1张图片

所以最小生成树的总边权为2+2+3=7

kruskal不断加小边，直到加到n-1条边图就变成了树。

#include 
#include 
#include 
#include 
#define MAXN 200005
using namespace std;
struct edge {
    int u,v,w;
}e[MAXN];
int n,m,tot;
int fa[MAXN];
bool comp(edge a,edge b) {
    return a.w

并查集

  • 题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

  • 输入输出格式

输入格式：

第一行包含两个整数N、M，表示共有N个元素和M个操作。
接下来M行，每行包含三个整数Zi、Xi、Yi
当Zi=1时，将Xi与Yi所在的集合合并
当Zi=2时，输出Xi与Yi是否在同一集合内，是的话输出Y；否则话输出N

输出格式：

如上，对于每一个Zi=2的操作，都有一行输出，每行包含一个大写字母，为Y或者N

  • 输入输出样例

输入样例#1：

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

输出样例#1：

N
Y
N
Y

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据，N<=10，M<=20；
对于70%的数据，N<=100，M<=1000；
对于100%的数据，N<=10000，M<=200000。

#include 
#include 
#include 
#define MAXN 10005
using namespace std;
int n,m,fa[MAXN];
int find(int x) {
    if(fa[x]!=x) return fa[x]=find(fa[x]);
}
void merge(int x,int y) {
    fa[find(x)]=fa[find(y)];
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++) {
        int opt,x,y;
        scanf("%d%d%d",&opt,&x,&y);
        if(opt==1) {
            if(find(x)!=find(y)) merge(x,y);
        }
        else {
            if(find(x)==find(y)) puts("Y");
            else puts("N");
        }
    }
    return 0;
}

单源最短路

  • 题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

  • 输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

  • 说明

时空限制：1000ms,128M
数据规模：
对于20%的数据：N<=5，M<=15
对于40%的数据：N<=100，M<=10000
对于70%的数据：N<=1000，M<=100000
对于100%的数据：N<=10000，M<=500000
样例说明：


考前的板子硬邦邦_第2张图片

SPFA

#include 
#include 
#include 
#define maxn 1001000
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct queue {
    int Q[500005],head,tail;
    queue() {
        head=0,tail=0;
    }
    void push(int a) {
        Q[++tail]=a;
        return ;
    }
    void pop() {
        head++;
        return ;
    }
    bool empty() {
        return head>=tail;
    }
    int front() {
        return Q[head+1];
    }
    int size() {
        if(head<=tail) return tail-head; 
    } 
};
struct Edge {
    int next,to,cost;
}e[maxn];
int num,head[maxn<<1],dist[maxn],vis[maxn],n,m,s;
void insert(int u,int v,int w) {
    num++;
    e[num].to=v;
    e[num].cost=w;
    e[num].next=head[u];
    head[u]=num;
}
void clearlove(){
    for(int i=0;i<=10010;i++)dist[i]=2147483647;
}
void spfa(int s) {
    clearlove();
    queue q;
    dist[s]=0;
    vis[s]=1;
    q.push(s);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=head[u];i;i=e[i].next) {
            int to=e[i].to;
            if(dist[to]>dist[u]+e[i].cost) {
                dist[to]=dist[u]+e[i].cost;
                if(!vis[to]) {
                    vis[to]=1;
                    q.push(to);
                }
            }
        }
    }
}
int main() {
    n=read(),m=read(),s=read();
    for(int i=1;i<=m;i++) {
        int u=read(),v=read(),w=read();
        insert(u,v,w);
    }
    spfa(s);
    for(int i=1;i<=n;i++)
    printf("%d ",dist[i]);
    return 0;
}

最近公共祖先（LCA）

  • 题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

  • 输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。
接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

  • 输入输出样例

输入样例#1：

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出样例#1：

4
4
1
4
4

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=10，M<=10
对于70%的数据：N<=10000，M<=10000
对于100%的数据：N<=500000，M<=500000
样例说明：
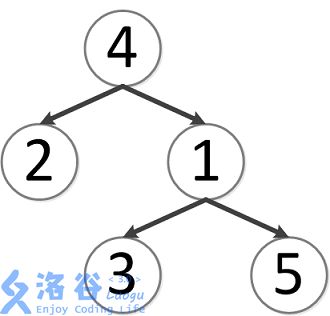
该树结构如下：

考前的板子硬邦邦_第3张图片

第一次询问：2、4的最近公共祖先，故为4。
第二次询问：3、2的最近公共祖先，故为4。
第三次询问：3、5的最近公共祖先，故为1。
第四次询问：1、2的最近公共祖先，故为4。
第五次询问：4、5的最近公共祖先，故为4。
故输出依次为4、4、1、4、4。
倍增 

#include 
#include 
#include 
#include 
#define MAXN 5000500
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge {
    int u,v,next;
}e[MAXN];
int num,head[MAXN],n,m,s;
int fa[MAXN][30],deep[MAXN];
void insert(int u,int v) {
    num++;
    e[num].v=v;
    e[num].next=head[u];
    head[u]=num;
}
void dfs(int x) {
    deep[x]=deep[fa[x][0]]+1;
    for(int i=0;fa[x][i];i++) fa[x][i+1]=fa[fa[x][i]][i];
    for(int i=head[x];i;i=e[i].next) {
        if(!deep[e[i].v]) {
            fa[e[i].v][0]=x;
            dfs(e[i].v);
        }
    }
}
int lca(int x,int y) {
    if(deep[x]>deep[y]) swap(x,y);
    for(int i=20;i>=0;i--) {
        if(deep[fa[y][i]]>=deep[x]) y=fa[y][i];
    }
    if(x==y) return x;
    for(int i=20;i>=0;i--) {
        if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
    }
    return fa[x][0];
}
int main() {
    n=read(),m=read(),s=read();
    for(int i=1;i

树链剖分

#include 
#include 
#include 
#include 
#include 
#define MAXN 500005
using namespace std;
int n,m,s,fa[MAXN],deep[MAXN],size[MAXN],top[MAXN];
vector vec[MAXN];
void dfs(int x) {
    size[x]=1;
    deep[x]=deep[fa[x]]+1;
    for(int i=0; isize[s])s=vec[x][i];
    }
    if(s) {
        top[s]=top[x];
        Get_heavy_edge(s);
    }
    for(int i=0;ideep[y]) swap(x,y);
    return x;
}
int main() {
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=n-1;i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        vec[u].push_back(v);
        vec[v].push_back(u);
    }
    dfs(s);
    Get_heavy_edge(s);
    for(int i=1;i<=m;i++) {
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));
    }
    return 0;
}

负环

  • 题目描述

暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索

  • 输入输出格式

输入格式：

第一行一个正整数T表示数据组数，对于每组数据：
第一行两个正整数N M，表示图有N个顶点，M条边
接下来M行，每行三个整数a b w，表示a->b有一条权值为w的边（若w<0则为单向，否则双向）

输出格式：

共T行。对于每组数据，存在负环则输出一行"YE5"(不含引号)，否则输出一行"N0"(不含引号)。

  • 输入输出样例

输入样例#1：

2
3 4
1 2 2
1 3 4
2 3 1
3 1 -3
3 3
1 2 3
2 3 4
3 1 -8

输出样例#1：

N0
YE5

说明

N,M,|w|≤200 000；1≤a,b≤N；T≤10 建议复制输出格式中的字符串。
此题普通Bellman-Ford或BFS-SPFA会TLE

#include 
#include 
#include 
#include 
#define MAXN 200005
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge {
    int u,v,w,next;
}e[MAXN<<1];
int n,m,t;
int num,head[MAXN<<1];
int vis[MAXN],dis[MAXN];
void insert(int u,int v,int w) {
    num++;
    e[num].v=v;
    e[num].next=head[u];
    e[num].w=w;
    head[u]=num;
}
void clear() {
    num=0;
    memset(e,0,sizeof(e));
    memset(head,0,sizeof(head));
    memset(dis,0,sizeof(dis));
    memset(vis,0,sizeof(vis));
}
bool spfa_dfs(int u) {
    vis[u]=1;
    for(int k=head[u];k;k=e[k].next) {
        int v=e[k].v,w=e[k].w;
        if(dis[u]+w

缩点

  • 题目背景

缩点+DP

  • 题目描述

给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

  • 输入输出格式

输入格式：

第一行，n,m
第二行，n个整数，依次代表点权
第三至m+2行，每行两个整数u,v，表示u->v有一条有向边

输出格式：

共一行，最大的点权之和。

  • 输入输出样例

输入样例#1：

2 2
1 1
1 2
2 1

输出样例#1：

2

  • 说明

n<=104,m<=105,|点权|<=1000 算法：Tarjan缩点+DAGdp

#include 
#include 
#include 
#include 
#include 
#define MAXN 10005
#define MAXM 500005
using namespace std;
struct edge {
    int u,v,next;
}e[MAXM<<1];
int num,head[MAXN<<1];
void ins(int u,int v) {
    num++;
    e[num].u=u;
    e[num].v=v;
    e[num].next=head[u];
    head[u]=num;
}
int cnt,DFN[MAXN],LOW[MAXN],Time,belong[MAXN],stack[MAXN],top;
bool inst[MAXN];
vector bcc[MAXN];
int n,m,w[MAXN],gg[MAXN];
void tarjan(int u) {
    LOW[u]=DFN[u]=++Time;
    inst[u]=true;
    stack[top++]=u;
    for(int i=head[u];i;i=e[i].next) {
        int v=e[i].v;
        if(inst[v]) {
            LOW[u]=min(LOW[u],DFN[v]);
        }
        else if(!DFN[v]) {
            tarjan(v);
            LOW[u]=min(LOW[u],LOW[v]);
        }
    }
    if(LOW[u]==DFN[u]) {
        int now;
        cnt++;
        do {
            now=stack[--top];
            inst[now]=false;
            belong[now]=cnt;
            bcc[cnt].push_back(now);
            w[cnt]+=gg[now];
        } while(now!=u);
    }
}
vector G[MAXN];
int du[MAXN];
void Shrinking_point() {
    for(int i=1;i<=m;i++) {
        int u=belong[e[i].u],v=belong[e[i].v];
        if(u!=v) G[u].push_back(v),du[v]++;
    }
}
struct queue {
    int Q[500005],head,tail;
    queue() {
        head=0,tail=0;
    }
    void push(int a) {
        Q[++tail]=a;
        return ;
    }
    void pop() {
        head++;
        return ;
    }
    bool empty() {
        return head>=tail;
    }
    int front() {
        return Q[head+1];
    }
    int size() {
        if(head<=tail) return tail-head; 
    } 
    void clear() {
        head=tail=0;
        memset(Q,0,sizeof(Q));
    }
};
int dist[MAXN],ans;
bool vis[MAXN];
void clearlove() {
    for(int i=0;i<=cnt;i++) dist[i]=0;
    fill(vis,vis+cnt+1,false);
}

int SPFA(int s) {
    int res=0;
    clearlove();
    queue q;
    dist[s]=w[s];
    vis[s]=1;
    q.push(s);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=0;i

割点

  • 题目背景

割点

  • 题目描述

给出一个n个点，m条边的无向图，求图的割点。

  • 输入输出格式

输入格式：

第一行输入n,m
下面m行每行输入x,y表示x到y有一条边

输出格式：

第一行输出割点个数
第二行按照节点编号从小到大输出节点，用空格隔开

  • 输入输出样例

输入样例#1：

6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6

输出样例#1：

1
5

  • 说明

n,m均为100000
tarjan 图不一定联通！！！

#include 
#include 
#include 
#include 
#define MAXN 100005
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge {
    int u,v,next;
}e[MAXN<<1];
int head[MAXN<<1],num;
void ins(int u,int v) {
    num++;
    e[num].u=u;
    e[num].v=v;
    e[num].next=head[u];
    head[u]=num;
}
int n,m,ans;
int dfn[MAXN],low[MAXN],Time;
bool cut[MAXN],in[MAXN];
int root,child;
void tarjan(int u,int fa) {
    int child=0;
    dfn[u]=low[u]=++Time;
    in[u]=true;
    for(int i=head[u];i;i=e[i].next) {
        int v=e[i].v;
        if(in[v] && v!=fa) {
            low[u]=min(low[u],dfn[v]);
        }
        else if(!dfn[v]) {
            tarjan(v,u);
            child++;
            low[u]=min(low[u],low[v]);
            if((fa!=root && dfn[u]<=low[v]) || (fa==root && child>1)) {
                if(!cut[u]) ans++;
                cut[u]=true;
            }
        }
    }
}
int main() {
    n=read(),m=read();
    for(int i=1;i<=m;i++) {
        int u=read(),v=read();
        ins(u,v);
        ins(v,u);
    }
    root=-1;
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,root);
    printf("%d\n",ans);
    for(int i=1;i<=n;i++) if(cut[i]) printf("%d ",i);
    return 0;
}

网络最大流

  • 题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

  • 输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

  • 输入输出样例

输入样例#1：

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1：

50

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=10，M<=25
对于70%的数据：N<=200，M<=1000
对于100%的数据：N<=10000，M<=100000
样例说明：


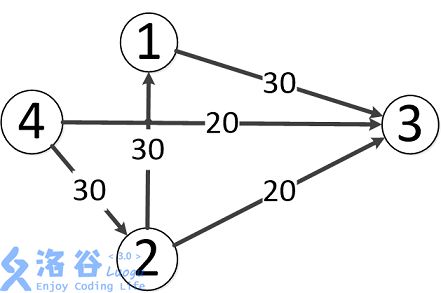
考前的板子硬邦邦_第4张图片
image

题目中存在3条路径：
4-->2-->3，该路线可通过20的流量
4-->3，可通过20的流量
4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）
故流量总计20+20+10=50。输出50。

#include 
#include 
#include 
#include 
#define MAXN 200005
#define MAXM 500005
#define INF 0x7fffffff
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge {
    int u,v,f,next;
}e[MAXN<<1];
int head[MAXN<<1],num;
void ins(int u,int v,int f) {
    num++;
    e[num].u=u;
    e[num].v=v;
    e[num].f=f;
    e[num].next=head[u];
    head[u]=num;
}
int n,m,S,T,ans;
int qu[MAXN<<1],deep[MAXN<<1];
bool bfs() {
    int h=0,t=1;
    memset(deep,-1,sizeof(deep));
    qu[h]=S;
    deep[S]=0;
    while(h

二分图匹配

  • 题目背景

二分图

  • 题目描述

给定一个二分图，结点个数分别为n,m，边数为e，求二分图最大匹配数

  • 输入输出格式

输入格式：

第一行，n,m,e
第二至e+1行，每行两个正整数u,v，表示u,v有一条连边

输出格式：

共一行，二分图最大匹配

  • 输入输出样例

输入样例#1：

1 1 1
1 1

输出样例#1：

1

  • 说明

网络流算法

#include 
#include 
#include 
#include 
#include 
#define MAXN 550000
using namespace std;
inline int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge {
    int to,next,v;
}e[550000];
int head[MAXN<<1],ne=1,q[MAXN<<1],h[MAXN<<1],ans,n,m,S,T,ee;
inline void ins(int u,int v,int f) {
    ne++;
    e[ne].to=v;
    e[ne].next=head[u];
    e[ne].v=f;
    head[u]=ne;
}
inline void insert(int u,int v,int f) {
    ins(u,v,f);ins(v,u,0);
}
bool bfs() {
    int t=0,w=1;
    memset(h,-1,sizeof(h));
    q[t]=S;h[S]=0;
    while(tm) continue;
        insert(u,v+n,1);
    }
    S=0,T=n+m+1;
    for(int i=1;i<=n;i++) insert(S,i,1);
    for(int i=1;i<=m;i++) insert(i+n,T,1);
    dinic();
    printf("%d",ans);
    return 0;
}

树状数组

  • 题目描述

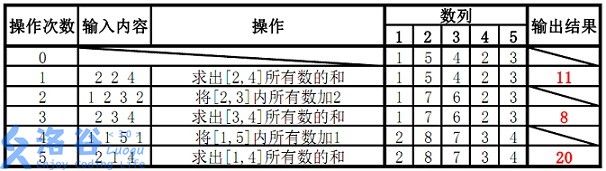
如题，已知一个数列，你需要进行下面两种操作：
1.将某一个数加上x
2.求出某区间每一个数的和

  • 输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数，表示一个操作，具体如下：
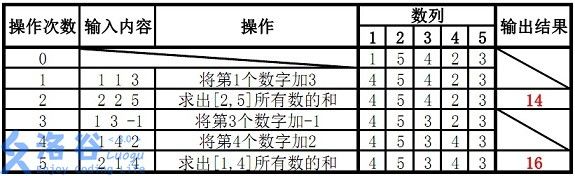
操作1： 格式：1 x k 含义：将第x个数加上k
操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

  • 输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出样例#1：

14
16

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=10000，M<=10000
对于100%的数据：N<=500000，M<=500000
样例说明：


考前的板子硬邦邦_第5张图片
image

故输出结果14、16

#include 
#include 
#include 
#define MAXN 500005
using namespace std;
int a[MAXN],c[MAXN],n,m;
int lowbit(int x) {
    return x&(-x);
}
void modify(int p,int x) {
    while(p<=n) {
        c[p]+=x;
        p+=lowbit(p);
    }
    return ;
}
int sum(int p) {
    int sum=0;
    while(p) {
        sum+=c[p];
        p-=lowbit(p);
    }
    return sum;
}
int query(int l,int r) {
    return sum(r)-sum(l-1);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),modify(i,a[i]);
    for(int i=1;i<=m;i++) {
        int id,x,y;
        scanf("%d%d%d",&id,&x,&y);
        if(id==1) modify(x,y); 
        else printf("%d\n",query(x,y));
    }
    return 0;
}

  • 题目描述

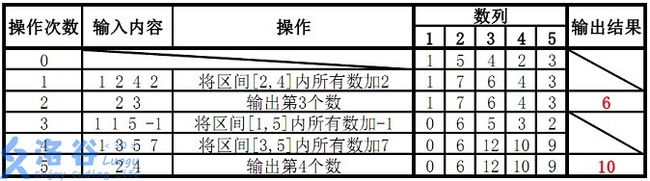
如题，已知一个数列，你需要进行下面两种操作：
1.将某区间每一个数数加上x
2.求出某一个数的和

  • 输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含2或4个整数，表示一个操作，具体如下：
操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k
操作2： 格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

  • 输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7

2 4

输出样例#1：

6
10

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=10000，M<=10000
对于100%的数据：N<=500000，M<=500000
样例说明：


考前的板子硬邦邦_第6张图片
image

故输出结果为6、10

#include 
#include 
#define maxn 500000+5
using namespace std;
int n,m,pre,c[maxn];
int lowbit(int x) {
    return x&(-x);
}
void modify(int pos,int x) {
    while(pos<=n) {
        c[pos]+=x;
        pos+=lowbit(pos);
    }
    return ;
}
int query(int pos) {
    int ans=0;
    while(pos>0) {
        ans+=c[pos];
        pos-=lowbit(pos);
    }
    return ans;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++) {
        int x;
        scanf("%d",&x);
        modify(i,x-pre);
        pre=x;
    }
    while(m--) {
        int id;
        scanf("%d",&id);
        if(id==1) {
            int l,r,k;
            scanf("%d%d%d",&l,&r,&k);
            modify(l,k);
            modify(r+1,-k);
        } else {
            int pos;
            scanf("%d",&pos);
            printf("%d\n",query(pos));
        }
    }
    return 0;
}

线段树

  • 题目描述

如题，已知一个数列，你需要进行下面两种操作：
1.将某区间每一个数加上x
2.求出某区间每一个数的和

  • 输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k
操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

  • 输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=1000，M<=10000
对于100%的数据：N<=100000，M<=100000
（数据已经过加强_，保证在int64/long long数据范围内）
样例说明：

考前的板子硬邦邦_第7张图片
image 

#include 
#include 
#include 
#include 
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define maxn 1000005
#define ll long long
using namespace std;
inline ll read() {
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
ll a[maxn],sum[maxn<<2],col[maxn<<2];
void update(ll rt) {
    sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void color(ll l,ll r,ll rt,ll c) {
    col[rt]+=c;
    sum[rt]+=c*(r-l+1);
}
void push_col(ll l,ll r,ll rt) {
    if(col[rt]) {
        ll m=(l+r)>>1;
        color(lson,col[rt]);
        color(rson,col[rt]);
        col[rt]=0;
    }
}
void build(ll l,ll r,ll rt) {
    if(l==r) {
        sum[rt] = a[l];
        return ;
    }
    ll m=(l+r)>>1;
    build(lson);
    build(rson);
    update(rt);
}
ll query(ll l,ll r,ll rt,ll L,ll R) {
    if(L<=l && R>=r)return sum[rt];
    push_col(l,r,rt);
    ll ret=0;
    ll m=(l+r)>>1;
    if(L<=m) ret+=query(lson,L,R);
    if(m=r) {
        color(l,r,rt,v);
        return ;
    }
    push_col(l,r,rt);
    ll m=(l+r)>>1;
    if(L<=m) modify(lson,L,R,v);
    if(m

  • 题目描述

如题，已知一个数列，你需要进行下面两种操作：
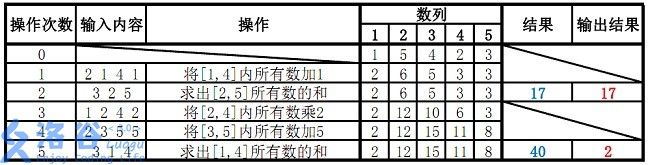
1.将某区间每一个数加上x
2.将某区间每一个数乘上x
3.求出某区间每一个数的和

  • 输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k
操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k
操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

  • 输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=8，M<=10
对于70%的数据：N<=1000，M<=10000
对于100%的数据：N<=100000，M<=100000
（数据已经过加强_）
样例说明：

考前的板子硬邦邦_第8张图片
image

故输出应为17、2（40 mod 38=2） 

#include 
using namespace std;
const long long maxn=1000000*4+10;
long long sum[maxn],add[maxn],mul[maxn];
#define root 1,n,1
#define ls l,m,o<<1
#define rs m+1,r,o<<1|1
inline void read(long long& x) {
    char c=getchar();
    long long p=1,n=0;
    while(c<'0'||c>'9') {
        if(c=='-')p=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9') {
        n=n*10+c-'0';
        c=getchar();
    }
    x=p*n;
}
long long ql,qr,val;
long long n,m,MOD;
inline void pushup(long long o) {
    sum[o]=(sum[o<<1]+sum[o<<1|1])%MOD;
}
inline void pushdown(long long o,long long m) {
    if(add[o]||mul[o]!=1) {
        long long ad=add[o],mu=mul[o];
        sum[o<<1]=(sum[o<<1]*mu+ad*(m-(m>>1)))%MOD;
        sum[o<<1|1]=(sum[o<<1|1]*mu+ad*(m>>1))%MOD;
        add[o<<1]=(add[o<<1]*mu+ad)%MOD;
        add[o<<1|1]=(add[o<<1|1]*mu+ad)%MOD;
        mul[o<<1]=(mul[o<<1]*mu)%MOD;
        mul[o<<1|1]=(mul[o<<1|1]*mu)%MOD;
        add[o]=0;
        mul[o]=1;
    }
}
void build(long long l,long long r,long long o) {
    add[o]=0;
    mul[o]=1;
    if(l==r) {
        read(sum[o]);
        sum[o]=sum[o]%MOD;
        return;
    }
    long long m=l+(r-l)/2;
    build(ls);
    build(rs);
    pushup(o);
}
void update_plus(long long l,long long r,long long o) {
    pushdown(o,r-l+1);
    if(ql<=l&&r<=qr) {
        add[o]+=val;
        add[o]=add[o]%MOD;
        sum[o]+=(r-l+1)*val;
        sum[o]=sum[o]%MOD;
        return;
    }
    long long m=l+(r-l)/2;
    if(ql<=m)update_plus(ls);
    if(qr>m)update_plus(rs);
    pushup(o);
}
void update_mul(long long l,long long r,long long o) {
    pushdown(o,r-l+1);
    if(ql<=l&&r<=qr) {
        mul[o]=mul[o]*val;
        mul[o]=mul[o]%MOD;
        sum[o]=sum[o]*val;
        sum[o]=sum[o]%MOD;
        return;
    }
    long long m=l+(r-l)/2;
    if(ql<=m)update_mul(ls);
    if(qr>m)update_mul(rs);
    pushup(o);
}
long long query(long long l,long long r,long long o) {
    pushdown(o,r-l+1);
    if(ql<=l&&r<=qr) {
        return sum[o];
    }
    long long m=l+(r-l)/2;
    long long ret=0;
    if(ql<=m)ret+=query(ls),ret=ret%MOD;
    if(qr>m)ret+=query(rs),ret=ret%MOD;
    return ret%MOD;
}
int main() {
    read(n);
    read(m);
    read(MOD);
    build(root);
    for(long long i=1; i<=m; i++) {
        long long op;
        read(op);
        if(op==1) {
            read(ql);
            read(qr);
            read(val);
            update_mul(root);
        }
        if(op==2) {
            read(ql);
            read(qr);
            read(val);
            update_plus(root);
        }
        if(op==3) {
            read(ql);
            read(qr);
            printf("%lld\n",query(root)%MOD);
        }
    }
    return 0;
}

ST表

  • 题目背景

这是一道ST表经典题——静态区间最大值
请注意最大数据时限只有0.8s，数据强度不低，请务必保证你的每次查询复杂度为O（1）

  • 题目描述

给定一个长度为N的数列，和M次询问，求出每一次询问的区间内数字的最大值。

  • 输入输出格式

输入格式：

第一行包含两个整数N,M，分别表示数列的长度和询问的个数。第二行包含N
个整数（记为ai​ ），依次表示数列的第i项。
接下来M 行，每行包含两个整数li​,ri​ ，表示查询的区间为[li​,ri​]

输出格式：

输出包含M 行，每行一个整数，依次表示每一次询问的结果。

输入输出样例

输入样例#1：

8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8

输出样例#1：

9
9
7
7
9
8
7
9

  • 说明

考前的板子硬邦邦_第9张图片
image.png 
#include 
#include 
#include 
#include 
#define MAXN 1000005
using namespace std;
int read() {
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m;
int st[MAXN][30],a[MAXN],log_2[MAXN];
inline void ini_st() {
    log_2[1]=0;
    for(int i=2;i<=n;++i) {
        log_2[i]=log_2[i-1];
        if((1<

矩阵快速幂

  • 题目背景

矩阵快速幂

  • 题目描述

给定n*n的矩阵A，求A^k

  • 输入输出格式

输入格式：

第一行，n,k
第2至n+1行，每行n个数，第i+1行第j个数表示矩阵第i行第j列的元素

输出格式：

输出A^k
共n行，每行n个数，第i行第j个数表示矩阵第i行第j列的元素，每个元素模10^9+7

  • 输入输出样例

输入样例#1：

2 1
1 1
1 1

输出样例#1：

1 1
1 1

  • 说明

n<=100, k<=10^12, |矩阵元素|<=1000 算法：矩阵快速幂

普通快速幂同理

#include 
#include 
#include 
#include 
#define ll long long
#define maxn 100+5
#define mod 1000000007
using namespace std;
ll n,m;
struct Matrix {
    ll a[maxn][maxn];
    void clear() {
        memset(a,0,sizeof(a));
    }
    Matrix() {
        this->clear();
    }
    Matrix operator *(const Matrix &b)const {
        Matrix c;
        for(ll i=0; i>=1,k=k*k)
        if (n&1) ret=ret*k;
    return ret;
}
int main() {
    Matrix x;
    cin>>n>>m;
    for(ll i=0; i>x.a[i][j];
    x=fastm(x,m);
    for(ll i=0; i

线性筛素数

  • 题目描述

如题，给定一个范围N，你需要处理M个某数字是否为质数的询问（每个数字均在范围1-N内）

  • 输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示查询的范围和查询的个数。
接下来M行每行包含一个不小于1且不大于N的整数，即询问该数是否为质数。

输出格式：

输出包含M行，每行为Yes或No，即依次为每一个询问的结果。

  • 输入输出样例

输入样例#1：

100 5
2
3
4
91
97

输出样例#1：

Yes
Yes
No
No
Yes

  • 说明

时空限制：500ms 128M
数据规模：
对于30%的数据：N<=10000，M<=10000
对于100%的数据：N<=10000000，M<=100000
样例说明：
N=100，说明接下来的询问数均不大于100且不小于1。
所以2、3、97为质数，4、91非质数。
故依次输出Yes、Yes、No、No、Yes。

#include 
#include 
#include 
#include 
using namespace std;
const int maxn=10000000;
int prime[maxn],n,tot,m;
bool vis[maxn];
bool is_prime(int x) {
    int k=sqrt(x+0.5);
    for(int i=2; i<=k; i++)
        if(x%i==0) return false;
    return true;
}
void Eratosthenes() { 
    int m=sqrt(n+0.5);
    vis[1]=true;
    for(int i=2; i<=m; i++)
        if(vis[i]==false)
            for(int j=i*i; j<=n; j+=i)
                vis[j]=true;
    return;
}
void GetPrime() { 
    for(int i=2; i<=n; i++) {
        if(vis[i]==false) prime[++tot]=i;
        for(int j=1; j<=tot&&i*prime[j]<=n; j++) {
            vis[i*prime[j]]=true;
            if(i%prime[j]==0) break;
        }
    }
    return;
}
void solve() {
    GetPrime();
    for(int i=1; i<=tot; i++)
        printf("%d ",prime[i]);
    return;
}
int main() {
    cin>>n>>m;
    Eratosthenes();
    while(m--) {
        int a;
        cin>>a;
        if(!vis[a]) cout<<"Yes"<

乘法逆元

  • 题目背景

这是一道模板题

  • 题目描述

给定n,p求1~n中所有整数在模p意义下的乘法逆元。

  • 输入输出格式

输入格式：
一行n,p

输出格式：
n行,第i行表示i在模p意义下的逆元。

  • 输入输出样例

输入样例#1：
10 13

输出样例#1：
1
7
9
10
8
11
2
5
3
4

  • 说明

image.png

线性 

#include
#define N 3000010
typedef long long ll;
using namespace std;
int inv[N],n,p;
int main() {
    cin>>n>>p;
    inv[1]=1;
    puts("1");
    for(int i=2; i<=n; i++) {
        inv[i]=(ll)(p-p/i)*inv[p%i]%p;
        printf("%d\n",inv[i]);
    }
    return 0;
}

扩展欧几里得

#include 
#include 
using namespace std;
int ex_gcd(int a,int b,int &x,int &y) {  
    if (a==0&&b==0) return -1;  
    if (b==0){x=1;y=0;return a;}  
    int d=ex_gcd(b,a%b,y,x);  
    y-=a/b*x;  
    return d;  
}  
  
int inv(int a,int n) {  
    int x,y;  
    int d = ex_gcd(a,n,x,y);  
    return (x%n+n)%n;  
}  
int main() {
    int a,p;
    scanf("%d%d",&a,&p);
    for(int i=1;i<=a;i++)
        printf("%d\n",inv(i,p));
    return 0;
}

扩展欧几里得（EXGCD）

  • 题目描述

求关于 x 的同余方程 ax ≡ 1 (mod b)的最小正整数解。

  • 输入输出格式

输入格式：

输入只有一行，包含两个正整数 a, b，用一个空格隔开。

输出格式：

输出只有一行，包含一个正整数 x0，即最小正整数解。输入数据保证一定有解。

  • 输入输出样例

输入样例#1：

3 10

输出样例#1：

7

  • 说明

【数据范围】
对于 40%的数据，2 ≤b≤ 1,000；
对于 60%的数据，2 ≤b≤ 50,000,000；
对于 100%的数据，2 ≤a, b≤ 2,000,000,000。

#include   
#include  
using namespace std;
int a,b,x,y,k;
void exgcd(int a,int b) {
    if(b==0) {
        x=1;
        y=0;
        return;
    }
    exgcd(b,a%b);
    k=x;
    x=y;
    y=k-a/b*y;
    return;
}
int main() {
    cin>>a>>b;
    exgcd(a,b);
    cout<<(x+b)%b;
    return 0;
}

字符串哈希

  • 题目描述

如题，给定N个字符串（第i个字符串长度为Mi，字符串内包含数字、大小写字母，大小写敏感），请求出N个字符串中共有多少个不同的字符串。
友情提醒：如果真的想好好练习哈希的话，请自觉，否则请右转PJ试炼场:)

  • 输入输出格式

输入格式：

第一行包含一个整数N，为字符串的个数。
接下来N行每行包含一个字符串，为所提供的字符串。

输出格式：

输出包含一行，包含一个整数，为不同的字符串个数。

  • 输入输出样例

输入样例#1：

5
abc
aaaa
abc
abcc
12345

输出样例#1：

4

  • 说明

时空限制：1000ms,128M
数据规模：
对于30%的数据：N<=10，Mi≈6，Mmax<=15;
对于70%的数据：N<=1000，Mi≈100，Mmax<=150
对于100%的数据：N<=10000，Mi≈1000，Mmax<=1500
样例说明：
样例中第一个字符串(abc)和第三个字符串(abc)是一样的，所以所提供字符串的集合为{aaaa,abc,abcc,12345}，故共计4个不同的字符串。

#include 
#include 
#include 
#include 
#define MAXN 10005
#define seed 20020207
#define ULL unsigned long long
using namespace std;
int n;
long long h[MAXN];
string s[MAXN];
ULL hash(string s) {
    ULL value=0;
    int x=1;
    for(int i=0;i>s[i];
        h[i]=hash(s[i]);
    }
    int ans=0;
    sort(h+1,h+n+1);
    for(int i=1;i<=n;i++) {
        if(h[i]!=h[i+1]) ans++;
    }
    printf("%d",ans);
    return 0;
}

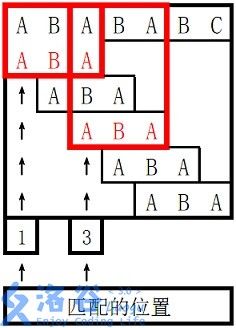
KMP

  • 题目描述

如题，给出两个字符串s1和s2，其中s2为s1的子串，求出s2在s1中所有出现的位置。
为了减少骗分的情况，接下来还要输出子串的前缀数组next。

  • 输入输出格式

输入格式：

第一行为一个字符串，即为s1
第二行为一个字符串，即为s2

输出格式：

若干行，每行包含一个整数，表示s2在s1中出现的位置
接下来1行，包括length(s2)个整数，表示前缀数组next[i]的值。

  • 输入输出样例

输入样例#1：

ABABABC
ABA

输出样例#1：
1
3
0 0 1

  • 说明

时空限制：1000ms,128M
数据规模：
设s1长度为N，s2长度为M
对于30%的数据：N<=15，M<=5
对于70%的数据：N<=10000，M<=100
对于100%的数据：N<=1000000，M<=1000000
样例说明：


考前的板子硬邦邦_第10张图片
image

所以两个匹配位置为1和3，输出1、3

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn=1001;
int Next[maxn];
vector Ans;
inline void Get_Next(string s) {
    int l=s.length(),t;
    Next[0]=-1;
    for(int i=1;i=0)
            t=Next[t];
        if(s[t+1]==s[i])
            Next[i]=t+1;
        else
            Next[i]=-1;
    }
}
inline void KMP(string s1,string s2) {
    Get_Next(s2);
    int l1=s1.length();
    int l2=s2.length();
    int i=0,j=0;
    while(j>s1>>s2;
    l=s2.length();
    KMP(s1,s2);
    for(int i=0;i

AC自动机

  • 题目背景

这是一道简单的AC自动机模板题。
用于检测正确性以及算法常数。
管理员提示：本题数据内有重复的单词，且重复单词应该计算多次，请各位注意

  • 题目描述

给定n个模式串和1个文本串，求有多少个模式串在文本串里出现过。

  • 输入输出格式

输入格式：

第一行一个n，表示模式串个数；
下面n行每行一个模式串；
下面一行一个文本串。

输出格式：

一个数表示答案

  • 输入输出样例

输入样例#1：

2
a
aa
aa

输出样例#1：

2

  • 说明

subtask1[50pts]:∑length(模式串)<=106,length(文本串)<=106,n=1；
subtask2[50pts]:∑length(模式串)<=106,length(文本串)<=106；

#include 
#include 
#include 
#include 
using namespace std;
struct Trie {
    int ch[26];
    int end;
    int fail;
}AC[1000000];
int cnt=0;
int index(char c) {
    return c-'a';
} 
void Build_Trie(string s) {
    int l=s.length();
    int now=0;
    for(int i=0;i q;
    for(int i=0;i<26;i++) {
        if(AC[0].ch[i]!=0) {
            AC[AC[0].ch[i]].fail=0;
            q.push(AC[0].ch[i]);
        }
    }
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        for(int i=0;i<26;i++) {
            if(AC[u].ch[i]!=0) {
                AC[AC[u].ch[i]].fail=AC[AC[u].fail].ch[i];
                q.push(AC[u].ch[i]);
            }
            else 
              AC[u].ch[i]=AC[AC[u].fail].ch[i];
        }
    }
}
int AC_work(string s) {
    int l=s.length();
    int now=0,ans=0;
    for(int i=0;i>s;
        Build_Trie(s);
    }
    Get_fail();
    cin>>s;
    printf("%d",AC_work(s));
    return 0;
}

  • 题目描述

有N个由小写字母组成的模式串以及一个文本串 T 。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串 T 中出现的次数最多。

  • 输入输出格式

输入格式：

输入含多组数据。
每组数据的第一行为一个正整数 N ，表示共有 N 个模式串， 1≤N≤150 。接下去 N 行，每行一个长度小于等于 70 的模式串。下一行是一个长度小于等于 106 的文本串 T 。
输入结束标志为 N=0 。

输出格式：

对于每组数据，第一行输出模式串最多出现的次数，接下去若干行每行输出一个出现次数最多的模式串，按输入顺序排列。

输入输出样例

输入样例#1：

2
aba
bab
ababababac
6
beta
alpha
haha
delta
dede
tata
dedeltalphahahahototatalpha
0

输出样例#1：

4
aba
2
alpha
haha

#include
#include
#include
#include
#include
#include
#include
using namespace std;
struct Tree {
    int fail;
    int vis[26];
    int end;
} AC[100000];
int cnt;
struct Result {
    int num;
    int pos;
} Ans[100000];
bool operator <(Result a,Result b) {
    if(a.num!=b.num)
        return a.num>b.num;
    else
        return a.pos Q;
    for(int i=0; i<26; ++i) {
        if(AC[0].vis[i]!=0) {
            AC[AC[0].vis[i]].fail=0;
            Q.push(AC[0].vis[i]);
        }
    }
    while(!Q.empty()) {
        int u=Q.front();
        Q.pop();
        for(int i=0; i<26; ++i) {
            if(AC[u].vis[i]!=0) {
                AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
                Q.push(AC[u].vis[i]);
            } else
                AC[u].vis[i]=AC[AC[u].fail].vis[i];
        }
    }
}
int AC_Query(string s) {
    int l=s.length();
    int now=0,ans=0;
    for(int i=0; i>n;
        if(n==0)break;
        cnt=0;
        Clean(0);
        for(int i=1; i<=n; ++i) {
            cin>>s[i];
            Ans[i].num=0;
            Ans[i].pos=i;
            Build(s[i],i);
        }
        AC[0].fail=0;
        Get_fail();
        cin>>s[0];
        AC_Query(s[0]);
        sort(&Ans[1],&Ans[n+1]);
        cout<

高精度

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define MAX_L 2005 //最大长度，可以修改
using namespace std;
class BN {
    public:
        int len, s[MAX_L];//数的长度，记录数组
//构造函数
        BN();
        BN(const char*);
        BN(int);
        bool sign;//符号 1正数 0负数
        string toStr() const;//转化为字符串，主要是便于输出
        friend istream& operator>>(istream &,BN &);//重载输入流
        friend ostream& operator<<(ostream &,BN &);//重载输出流
//重载复制
        BN operator=(const char*);
        BN operator=(int);
        BN operator=(const string);
//重载各种比较
        bool operator>(const BN &) const;
        bool operator>=(const BN &) const;
        bool operator<(const BN &) const;
        bool operator<=(const BN &) const;
        bool operator==(const BN &) const;
        bool operator!=(const BN &) const;
//重载四则运算
        BN operator+(const BN &) const;
        BN operator++();
        BN operator++(int);
        BN operator+=(const BN&);
        BN operator-(const BN &) const;
        BN operator--();
        BN operator--(int);
        BN operator-=(const BN&);
        BN operator*(const BN &)const;
        BN operator*(const int num)const;
        BN operator*=(const BN&);
        BN operator/(const BN&)const;
        BN operator/=(const BN&);
//四则运算的衍生运算
        BN operator%(const BN&)const;//取模（余数）
        BN factorial()const;//阶乘
        BN Sqrt()const;//整数开根（向下取整）
        BN pow(const BN&)const;//次方
//一些乱乱的函数
        void clean();
        ~BN();
};
#define max(a,b) a>b ? a : b
#define min(a,b) a>(istream &in, BN &num) {
    string str;
    in>>str;
    num=str;
    return in;
}
ostream &operator<<(ostream &out, BN &num) {
    out<= 0; i--)
        if (s[i] != num.s[i])
            return sign ? (s[i] < num.s[i]) : (!(s[i] < num.s[i]));
    return !sign;
}
bool BN::operator>(const BN&num)const {
    return num < *this;
}
bool BN::operator<=(const BN&num)const {
    return !(*this>num);
}
bool BN::operator>=(const BN&num)const {
    return !(*this num || *this < num;
}
bool BN::operator==(const BN&num)const {
    return !(num != *this);
}
BN BN::operator+(const BN &num) const {
    if (sign^num.sign) {
        BN tmp = sign ? num : *this;
        tmp.sign = 1;
        return sign ? *this - tmp : num - tmp;
    }
    BN result;
    result.len = 0;
    int temp = 0;
    for (int i = 0; temp || i < (max(len, num.len)); i++) {
        int t = s[i] + num.s[i] + temp;
        result.s[result.len++] = t % 10;
        temp = t / 10;
    }
    result.sign = sign;
    return result;
}
BN BN::operator++() {
    *this = *this + 1;
    return *this;
}
BN BN::operator++(int) {
    BN old = *this;
    ++(*this);
    return old;
}
BN BN::operator+=(const BN &num) {
    *this = *this + num;
    return *this;
}
BN BN::operator-(const BN &num) const {
    BN b=num,a=*this;
    if (!num.sign && !sign) {
        b.sign=1;
        a.sign=1;
        return b-a;
    }
    if (!b.sign) {
        b.sign=1;
        return a+b;
    }
    if (!a.sign) {
        a.sign=1;
        b=BN(0)-(a+b);
        return b;
    }
    if (a= 0) g = 0;
        else {
            g = 1;
            x += 10;
        }
        result.s[result.len++] = x;
    }
    result.clean();
    return result;
}
BN BN::operator * (const BN &num)const {
    BN result;
    result.len = len + num.len;
    for (int i = 0; i < len; i++)
        for (int j = 0; j < num.len; j++)
            result.s[i + j] += s[i] * num.s[j];
    for (int i = 0; i < result.len; i++) {
        result.s[i + 1] += result.s[i] / 10;
        result.s[i] %= 10;
    }
    result.clean();
    result.sign = !(sign^num.sign);
    return result;
}
BN BN::operator*(const int num)const {
    BN x = num;
    BN z = *this;
    return x*z;
}
BN BN::operator*=(const BN&num) {
    *this = *this * num;
    return *this;
}
BN BN::operator /(const BN&num)const {
    BN ans;
    ans.len = len - num.len + 1;
    if (ans.len < 0) {
        ans.len = 1;
        return ans;
    }
    BN divisor = *this, divid = num;
    divisor.sign = divid.sign = 1;
    int k = ans.len - 1;
    int j = len - 1;
    while (k >= 0) {
        while (divisor.s[j] == 0) j--;
        if (k > j) k = j;
        char z[MAX_L];
        memset(z, 0, sizeof(z));
        for (int i = j; i >= k; i--)
            z[j - i] = divisor.s[i] + '0';
        BN dividend = z;
        if (dividend < divid) {
            k--;
            continue;
        }
        int key = 0;
        while (divid*key <= dividend) key++;
        key--;
        ans.s[k] = key;
        BN temp = divid*key;
        for (int i = 0; i < k; i++)
            temp = temp * 10;
        divisor = divisor - temp;
        k--;
    }
    ans.clean();
    ans.sign = !(sign^num.sign);
    return ans;
}
BN BN::operator/=(const BN&num) {
    *this = *this / num;
    return *this;
}
BN BN::operator%(const BN& num)const {
    BN a = *this, b = num;
    a.sign = b.sign = 1;
    BN result, temp = a / b*b;
    result = a - temp;
    result.sign = sign;
    return result;
}
BN BN::pow(const BN& num)const {
    BN result = 1;
    for (BN i = 0; i < num; i++)
        result = result*(*this);
    return result;
}
BN BN::factorial()const {
    BN result = 1;
    for (BN i = 1; i <= *this; i++)
        result *= i;
    return result;
}
void BN::clean() {
    if (len == 0) len++;
    while (len > 1 && s[len - 1] == '\0')
        len--;
}
BN BN::Sqrt()const {
    if(*this<0)return -1;
    if(*this<=1)return *this;
    BN l=0,r=*this,mid;
    while(r-l>1) {
        mid=(l+r)/2;
        if(mid*mid>*this)
            r=mid;
        else
            l=mid;
    }
    return l;
}
BN::~BN() {
}
int main() {return 0;}

目前想到的只有这些啦
如果有遗漏考场上现yy吧

预祝NOIp2017 RP++ 頑張って！
flag：拿了1=我就女装给你们看

你可能感兴趣的:(考前的板子硬邦邦)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • 情绪觉察日记第37天 露露_e800
    今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
  • 芦花鞋一四 许叶晗
    又是在一个寒冷的夏日里，青铜和葵花决定今天一起去卖芦花鞋，奶奶亲手给他们做了一碗热乎乎的粥对他们说:“就靠你们两挣生活费了这碗粥赶紧趁热喝了吧！”于是青铜和葵花喝完了奶奶给她们做的粥，就准备去镇上卖卢花鞋，这回青铜和葵花穿着新的芦花鞋来到了镇上。青铜这回看到了很多人都在卖，用手势表达对葵花说:“这回有好多人在抢我们生意呢！我们必须得吆喝起来。”葵花点了点头。可是谁知他们也大声的叫，卖芦花喽！卖芦花
  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 关于沟通这件事，项目经理不需要每次都面对面进行 流程大师兄
    很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 铭刻于星（四十二） 随风至
    69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
  • 底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说 造命者说
    底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说我叫吴起，生于公元前440年的战国初期，正是群雄并起、天下纷争不断的时候。后人说我是军事家、政治家、改革家，是兵家代表人物。评价我一生历仕鲁、魏、楚三国，通晓兵家、法家、儒家三家思想，在内政军事上都有极高的成就。周安王二十一年（公元前381年），因变法得罪守旧贵族，被人乱箭射死。我出生在卫国一个“家累万金”的富有家庭，从年轻时候起就不甘平凡
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 随笔 | 仙一般的灵气 海思沧海
    仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
  • 想家 爆米花机
    也许不同于大家对家乡的思念，我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福，我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女，我贪恋家的安逸。刚刚踏出大学校门，初出茅庐，无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气，是无法适应工作的节奏，是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志，选择再次踏上征程。图片发自App
  • 【iOS】MVC设计模式 Magnetic_h iosmvc设计模式objective-c学习ui
    MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
  • OC语言多界面传值五大方式 Magnetic_h iosui学习objective-c开发语言
    前言在完成暑假仿写项目时，遇到了许多需要用到多界面传值的地方，这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值，简单地说就是通过访问后一个视图控制器的属性来为它赋值，通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • UI学习——cell的复用和自定义cell Magnetic_h ui学习
    目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
  • element实现动态路由+面包屑 软件技术NINI vue案例vue.js前端
    el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
  • 10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
    本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
  • C语言宏函数 南林yan C语言c语言
    一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
  • 地推话术，如何应对地推过程中家长的拒绝 校师学
    相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务java架构
    在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • 瑶池防线 谜影梦蝶
    冥华虽然逃过了影梦的军队，但他是一个忠臣，他选择上报战况。败给影梦后成逃兵，高层亡尔还活着，七重天失守......随便一条，即可处死冥华。冥华自然是知道以仙界高层的习性此信一发自己必死无疑，但他还选择上报实情，因为责任。同样此信送到仙宫后，知道此事的人，大多数人都认定冥华要完了，所以上到仙界高层，下到扫大街的，包括冥华自己，全都准备好迎接冥华之死。如果仙界现在还属于两方之争的话，冥华必死无疑。然而
  • 爬山后遗症 璃绛
    爬山，攀登，一步一步走向制高点，是一种挑战。成功抵达是一种无法言语的快乐，在山顶吹吹风，看看风景，这是从未有过的体验。然而，爬山一时爽，下山腿打颤，颠簸的路，一路向下走，腿部力量不够，走起来抖到不行，停不下来了！第二天必定腿疼，浑身酸痛，坐立难安！
  • ztree异步加载 3213213333332132 JavaScriptAjaxjsonWebztree
    相信新手用ztree的时候,对异步加载会有些困惑，我开始的时候也是看了API花了些时间才搞定了异步加载，在这里分享给大家。 我后台代码生成的是json格式的数据，数据大家按各自的需求生成，这里只给出前端的代码。 设置setting，这里只关注async属性的配置 var setting = { //异步加载配置
  • thirft rpc 具体调用流程 BlueSkator 中间件rpcthrift
    Thrift调用过程中，Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类，这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作：         （1）     将客户端程序调用的函数名和参数传递给协议层（TProtocol），协议
  • 异或运算推导, 交换数据 dcj3sjt126com PHP异或^
    /* * 5 0101 * 9 1010 * * 5 ^ 5 * 0101 * 0101 * ----- * 0000 * 得出第一个规律: 相同的数进行异或, 结果是0 * * 9 ^ 5 ^ 6 * 1010 * 0101 * ---- * 1111 * * 1111 * 0110 * ---- * 1001
  • 事件源对象 周华华 JavaScript
    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&q
  • MySql配置及相关命令 g21121 mysql
            MySQL安装完毕后我们需要对它进行一些设置及性能优化，主要包括字符集设置，启动设置，连接优化，表优化，分区优化等等。           一 修改MySQL密码及用户      
  • [简单]poi删除excel 2007超链接 53873039oycg Excel
          采用解析sheet.xml方式删除超链接，缺点是要打开文件2次,代码如下:      public void removeExcel2007AllHyperLink(String filePath) throws Exception { OPCPackage ocPkg = OPCPac
  • Struts2添加 open flash chart 云端月影
    准备以下开源项目： 1. Struts 2.1.6 2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009) 3. jofc2，这东西不知道是没做好还是什么意思，好像和ofc2不怎么匹配，最好下源码，有什么问题直接改。 4. log4j 用eclipse新建动态网站，取名OFC2Demo，将Struts2 l
  • spring包详解 aijuans spring
    下载的spring包中文件及各种包众多，在项目中往往只有部分是我们必须的，如果不清楚什么时候需要什么包的话，看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包，关于发布包下面会详细进行说明。 docs&nb
  • 网站推广之seo概念 antonyup_2006 算法Web应用服务器搜索引擎Google
       持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时，准备了解下网站的推广分析策略。     所谓网站推广，目的在于让尽可能多的潜在用户了解并访问网站，通过网站获得有关产品和服务等信息，为最终形成购买决策提供支持。     网站推广策略有很多，seo，email，adv
  • 单例模式,sql注入,序列 百合不是茶 单例模式序列sql注入预编译
      序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时 需要使用序列创建一个自增长的字段  居然不会了,所以将序列写在本篇的前面    1,序列是一个保存数据连续的增长的一种方式; 序列的创建; CREATE SEQUENCE seq_pro 2 INCREMENT BY 1 -- 每次加几个 3
  • Mockito单元测试实例 bijian1013 单元测试mockito
    Mockito单元测试实例： public class SettingServiceTest { private List<PersonDTO> personList = new ArrayList<PersonDTO>(); @InjectMocks private SettingPojoService settin
  • 精通Oracle10编程SQL(9)使用游标 bijian1013 oracle数据库plsql
    /* *使用游标 */ --显示游标 --在显式游标中使用FETCH...INTO语句 DECLARE CURSOR emp_cursor is select ename,sal from emp where deptno=1; v_ename emp.ename%TYPE; v_sal emp.sal%TYPE; begin ope
  • 【Java语言】动态代理 bit1129 java语言
      JDK接口动态代理 JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式，为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联   package com.tom; import com.tom.model.User; import com.tom.service.IUserService;
  • Java通信之URL通信基础 白糖_ javajdkwebservice网络协议ITeye
    java对网络通信以及提供了比较全面的jdk支持，java.net包能让程序员直接在程序中实现网络通信。 在技术日新月异的现在，我们能通过很多方式实现数据通信，比如webservice、url通信、socket通信等等，今天简单介绍下URL通信。 学习准备：建议首先学习java的IO基础知识   URL是统一资源定位器的简写，URL可以访问Internet和www，可以通过url
  • 博弈Java讲义 - Java线程同步 (1) boyitech java多线程同步锁
      在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件，共用数据库连接，全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。    同步不仅可以阻止一个线程看到对象处于不一致的状态，它还可以保证进入同步方法或者块的每个线程，都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件（cri
  • java-给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 bylijinnan java
    public class DeleteExtraSpace { /** * 题目：给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 * 方法1.用已有的String类的trim和replaceAll方法 * 方法2.全部用正则表达式，这个我不熟 * 方法3.“重新发明轮子”，从头遍历一次 */ public static v
  • An error has occurred.See the log file错误解决！ Kai_Ge MyEclipse
    今天早上打开MyEclipse时，自动关闭！弹出An error has occurred.See the log file错误提示！ 很郁闷昨天启动和关闭还好着！！！打开几次依然报此错误，确定不是眼花了！ 打开日志文件！找到当日错误文件内容： --------------------------------------------------------------------------
  • [矿业与工业]修建一个空间矿床开采站要多少钱? comsci
           地球上的钛金属矿藏已经接近枯竭...........        我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床.....        那么,现在要编制一个预算,提交给财政部门..
  • 解析Google Map Routes dai_lm google api
    为了获得从A点到B点的路劲，经常会使用Google提供的API，例如 [url] http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false [/url] 从返回的结果上，大致可以了解应该怎么走，但
  • SQL还有多少“理所应当”？ datamachine sql
    转贴存档，原帖地址：http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html！ ------------------------------------华丽的分割线--------------------------------
  • Yii使用Ajax验证时，如何设置某些字段不需要验证 dcj3sjt126com Ajaxyii
    经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如: $form=$this->beginWidget('CActiveForm', array(        'id'=>'usuario-form',&
  • 使用git同步网站代码 dcj3sjt126com crontabgit
    转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com   管理一网站，最开始使用的虚拟空间，采用提供商支持的ftp上传网站文件，后换用vps，vps可以自己搭建ftp的，但是懒得搞，直接使用scp传输文件到服务器，现在需要更新文件到服务器，使用scp真的很烦。发现本人就职的公司，采用的git+rsync的方式来管理、同步代码，遂
  • sql基本操作 蕃薯耀 sqlsql基本操作sql常用操作
    sql基本操作 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年6月1日 17:30:33 星期一     &
  • Spring4+Hibernate4+Atomikos3.3多数据源事务管理 hanqunfeng Hibernate4
    Spring3+后不再对JTOM提供支持，所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考：http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站：http://www.atomikos.com/   一.pom.xml <dependency> <
  • jquery中两个值得注意的方法one()和trigger()方法 jackyrong trigger
      在jquery中，有两个值得注意但容易忽视的方法，分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍 1） one方法     one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数，格式为    one(type,${data},fn) &nb
  • 拿工资不仅仅是让你写代码的 lampcy 工作面试咨询
    这是我对团队每个新进员工说的第一件事情。这句话的意思是，我并不关心你是如何快速完成任务的，哪怕代码很差，只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。 这个说法其实很合理：我们的工作是思考客户提出的问题，然后制定解决方案。思考第一，代码第二，公司请我们的最终目的不是写代码，而是想出解决方案。 话粗理不粗。 付你薪水不是让你来思考的，也不是让你来写代码的，你的目的是交付产品
  • 架构师之对象操作----------对象的效率复制和判断是否全为空 nannan408 架构师
    1.前言。   如题。 2.代码。 (1)对象的复制，比spring的beanCopier在大并发下效率要高，利用net.sf.cglib.beans.BeanCopier Src src=new Src(); BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
  • ajax 被缓存的解决方案 Rainbow702 JavaScriptjqueryAjaxcache缓存
    使用jquery的ajax来发送请求进行局部刷新画面，各位可能都做过。 今天碰到一个奇怪的现象，就是，同一个ajax请求，在chrome中，不论发送多少次，都可以发送至服务器端，而不会被缓存。但是，换成在IE下的时候，发现，同一个ajax请求，会发生被缓存的情况，只有第一次才会被发送至服务器端，之后的不会再被发送。郁闷。 解决方法如下： ① 直接使用 JQuery提供的 “cache”参数，
  • 修改date.toLocaleString()的警告 tntxia String
      我们在写程序的时候，经常要查看时间，所以我们经常会用到date.toLocaleString()，但是date.toLocaleString()是一个过时 的API，代替的方法如下：   package com.tntxia.htmlmaker.util; import java.text.SimpleDateFormat; import java.util.
  • 项目完成后的小总结 xiaomiya js总结项目
    项目完成了，突然想做个总结但是有点无从下手了。 做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。 先说说项目主要实现的功能吧 1，按键精灵 2，获取行情数据 3，各种input输入条件判断 4，发送数据（有json格式和string格式） 5，获取预警条件列表和预警结果列表， 6，排序， 7，预警结果分页获取 8，导出文件（excel，text等） 9，修
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他