树(Tree)的基本概念
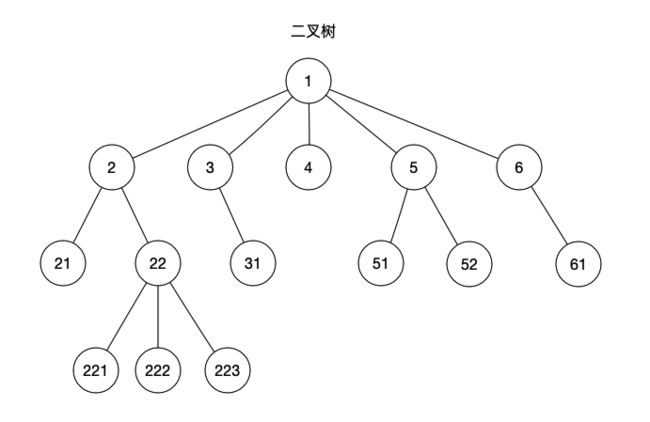
首先来介绍一些树的基本概念,二叉树的结构如下图所示:
- 节点:图中的每一个圆形都是节点;
- 根节点:1是当前二叉树的根节点,一棵树最多只有一个根节点;
- 父节点:1是2,3,4,5,6的父节点,2是21,22的父节点;
- 子节点:2,3,4,5,6是1的子节点;
- 兄弟节点:同一个父节点的节点之间是兄弟节点,2,3,4,5,6是兄弟节点;
- 一棵树可以没有任何节点,称之为空树;
- 一棵树可以只有一个节点,也就是只有根节点;
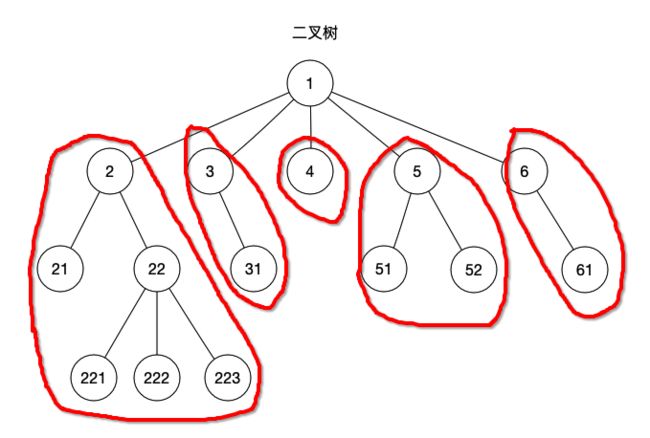
- 子树:红圈圈出来的是节点1的5个子树;
- 左子树:节点2下面的21是属于左子树;
- 右子树:节点2下面的22是属于右子树;
- 节点的度(degree):子树的个数;节点2有两个子树,则其度为2,节点3只有一个子树,则其度为1;节点4没有子树,则其度为0;
- 树的度:所有节点度中的最大值,如图易知树的度为5;
- 叶子节点(leaf):度为0的节点;4,21,31,51,52,61,221,222,223都是叶子节点;
- 层数(level):根节点在第一层,根节点的子节点在第二层,以此类推;
- 节点的深度(depth):从根节点到当前节点的唯一路径上的节点总数;31节点从根节点开始路径为1-3-31,其深度为3;223节点从根节点开始路径为1-2-22-223,其深度为4;
- 节点的高度(height):从当前节点到最远叶子节点的路径上的节点总数;2节点到最远的叶子节点有221,222,223,到221的路径为2-22-221,则其高度为3;
- 树的深度:所有节点深度中的最大值;易知此树的深度为4;
- 树的高度:所有节点高度中的最大值;易知此树的高度为4;
- 树的深度 等于 树的高度;
- 有序树:树中任意节点的子节点之间有顺序关系;
- 无序树:树中任意节点的子节点之间没有顺序关系,也可称为自由树;
- 森林:由m(m >= 0)棵互不相交的树组成的集合;
二叉树及其性质
- 二叉树的每个节点的度最大为2,即最多拥有2棵子树;
- 二叉树的左子树与右子树是有顺序的;
- 二叉树即使某个节点只有一棵子树,也要区分左右子树;
- 非空二叉树的第i层,最多有2^(i-1)个节点(i >=1);
- 在高度为h的二叉树上,最多有2^h-1个节点(h >=1);
- 对于任何一棵非空二叉树,如果叶子节点个数为n0,度为2的节点个数为n2,则有n0 = n2 + 1;
- 假设度为1的节点个数为n1,那么二叉树的节点总数n = n0 + n1 + n2;
- 二叉树的总边数T = n1 + n2 * 2 = n - 1 = n0 + n1 + n2 - 1,所以有n0 = n2 + 1;(边是指箭头指向联系父节点与子节点)
- 真二叉树(Proper Binary Tree):所有节点的度要么为0,要么为2;如下图所示:
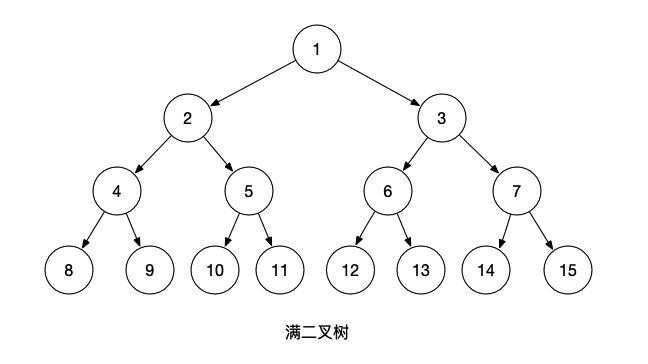
- 满二叉树(Full Binary Tree):所有节点的度要么为0,要么为2,且所有叶子节点都在最后一层;如下图所示:
在同样高度的二叉树中,满二叉树的叶子节点数量最多,总节点数量最多;
满二叉树一定是真二叉树,真二叉树不一定是满二叉树;
假设满二叉树的高度为h(h >= 1),那么第i层的节点数量为2^(i-1); 叶子节点数量为:2^(h-1), 叶子节点肯定在第h层;总节点数量为(2^h -1)
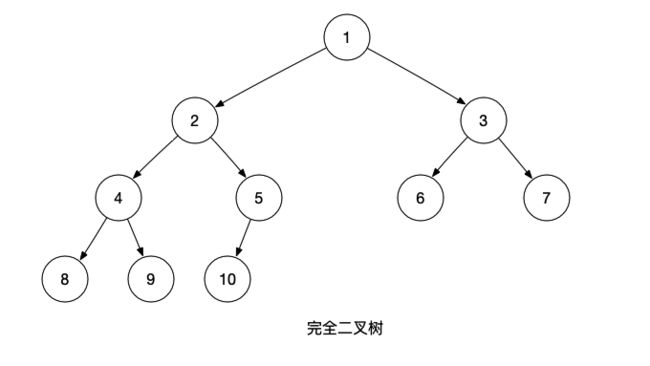
完全二叉树(Complete Binary Tree):叶子节点只会出现在最后两层,且最后一层的叶子节点都靠左对齐;如下图所示:
- 完全二叉树的节点从上往下,从左到右排列;
- 完全二叉树从根节点至倒数第二层是一棵满二叉树;
- 满二叉树一定是一棵完全二叉树,完全二叉树不一定是满二叉树;
完全二叉树的性质
- 度为1的节点只有左子树;
- 度为1的节点要么是1个,要么是0个;
- 同样节点数量的二叉树,完全二叉树的高度最小,与完全二叉树节点的排列有关;
- 假设完全二叉树的高度为h(h >= 1),
- 那么至少有2^(h-1)个节点, (2^0 + 2^1 + 2^2 +...+ 2^(h-2) +1);
- 最多有2^h-1(满二叉树);
- 若总节点数量为n,那么 2^(h-1) <= n < 2^h,取对数则有:(h-1) <= log2(n) < h,由于h只能是整数,那么n = log2(n)向下取整+1,即n = floor(log2(n)) + 1;
- floor函数是向下取整,ceiling函数是向上取整;
- 一棵有n个节点的完全二叉树(n>0),从上到下,从左到右从节点1开始进行编号,对任意第i个节点:
- 如果i = 1,它是根节点;
- 如果i > 1,它的父节点编号为floor(i/2);
- 如果2i <= n,那么它的左子节点编号为2i;
- 如果2i + 1 <= n,那么它的右子节点编号为2i+1;
- 如果2i + 1 > n,那么它没有右子节点;
面试题
第一道:如果一棵完全二叉树有768个节点,求其叶子节点的个数。
- 对于任何一棵非空二叉树,如果叶子节点个数为n0,度为2的节点个数为n2,则有n0 = n2 + 1;
- 假设度为1的节点个数为n1,那么总节点数n = n0 + n1 + n2 ;
- 那么 n = n0 + n1 +n0 - 1 = 2n0 + n1 - 1
- 又因为完全二叉树 度为1的节点要么是1个,要么是0个;
- 当n1 = 0时,n = 2n0 - 1,则n为奇数,不符合条件;
- 当n1 = 1时,n = 2n0,则n为偶数符合条件,所以叶子节点n0 = 384
根据上面的推断进行总结:
- 一棵完全二叉树有n个节点,
- 若n为奇数,那么叶子节点的数量n0 = (n + 1)/2
- 若n为偶数,那么叶子节点的数量n0 = n/2
- 叶子节点数量n0 = floor((n + 1)/2) = ceiling(n/2)
- 非叶子节点个数为 n1 + n2 = floor(n/2) = ceiling((n - 1)/2)
二叉树的遍历
根据节点访问顺序的不同,二叉树的常见遍历方式有4种:
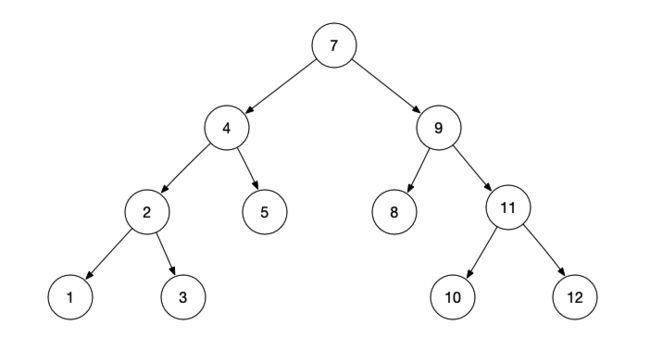
二叉树如下所示:
1.前序遍历:Preorder Traversal
- 访问顺序为:先访问根节点,然后遍历左子树,最后遍历右子树,递归的过程;
- 上面二叉树前序遍历的顺序为:7->4->2->1->3->5->9->8->11->10->12
2.中序遍历:Inorder Traversal
- 访问顺序为:先遍历左子树,然后访问根节点,最后遍历右子树,递归的过程;
- 上面二叉树前序遍历的顺序为:1->2->3->4->5->7->8->9->10->11->12
3. 后序遍历:Postorder Traversal
- 访问顺序为:先遍历左子树,然后遍历右子树,最后访问根节点,递归的过程;
- 上面二叉树 后序遍历的顺序为:1->3->2->5->4->8->10->12->11->9->7
4. 层序遍历:Level Order Traversal
- 访问顺序为:从上到下,从左到右,依次访问每一个节点;使用队列Queue
- 将根节点入队;
- 循环执行一下操作,直到队列为空;
- 将队头节点A出队,进行访问;
- 将A的左子节点入队;
- 将A的右子节点入队。
- 上面二叉树 后序遍历的顺序为:7->4->9->2->5->8->11->1->3->10->12
重构二叉树
- 前序遍历+中序遍历 确定唯一的二叉树;
- 前序遍历+后序遍历,如果二叉树是真二叉树,结果是唯一的;否则结果不唯一;
- 后序遍历+中序遍历 确定唯一的二叉树。
前驱节点
- 中序遍历时,当前节点node的前一个节点;
- 寻找node的前驱节点,逻辑如下:
-
当node左子节点不为空时,即node.left != null:- node = node.left.right.right....,不断的去取node的左子节点的右节点,赋值给node;
- 终止条件:当node = null时,找到其前驱节点,preNode = node;
-
当node左子节点为空且父节点不为空时,即node.left = null && node.parent != null- node = node.parent.parent.parent....,不断的去取node的父节点,并赋值给node;
- 终止条件:当node是其父节点parent的右节点时终止;找到其前驱节点,preNode = node;
当node.left == null && node.parent == null- 此节点没有前驱节点
后继节点
- 中序遍历时,当前节点的后一个节点
- 寻找后继节点,逻辑如下:
-
当node的右子节点不为空时,即node.right != null:- node = node.right.left.left.left....,不断的去取node的右子节点的左节点,赋值给node;
- 终止条件:当node = null,找到其后继节点,succeedNode = node;
-
当node右子节点为空且父节点不为空时,即node.right == null && node.parent != null:- node = node.parent.parent.parent..., 不断的去取node的父节点,并赋值给node,
- 终止条件:当node是其父节点parent的左节点时终止;找到其后继节点,succeedNode = node.parent;
-
当node.right == null && node.parent == null:- 此节点没有后继节点
二叉树的接口设计
- 存储元素的数量;
- 是否为空;
- 添加元素;
- 删除元素;
- 清空元素;
- 是否包含某个元素;
- 遍历节点元素;
代码实现如下:
import java.util.LinkedList;
import java.util.Queue;
public class YYBinaryTree {
/**
* 元素数量
*/
protected int size;
/**
* 根节点
*/
protected Node root;
/**
* 内部类 -- 节点
* @param
*/
protected static class Node{
/**
* 数据元素
*/
E element;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
/**
* 父节点
*/
Node parent;
public Node(E element, Node parent) {
this.element = element;
this.parent = parent;
}
/**
* 是否是叶子节点
* @return
*/
public boolean isLeaf(){
return left == null && right == null;
}
/**
* 拥有左右两个子节点
* @return
*/
public boolean hasTwoNode(){
return left != null && right != null;
}
/**
* 判断当前节点是否是父节点的左子节点
* @return
*/
public boolean isLeftChild(){
return parent != null && this == parent.left;
}
/**
* 判断当前节点是否是父节点的右子节点
* @return
*/
public boolean isRightChild(){
return parent != null && this == parent.right;
}
}
/**
* 抽象类
*/
public static abstract class Visitor{
boolean stop;
public abstract boolean visit(E element);
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
/**
* 前序遍历
*/
public void preorderTraversal(Visitor visitor){
if (visitor == null) return;
preorderTraversal(root,visitor);
}
private void preorderTraversal(Node node, Visitor visitor){
if (node == null || visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorderTraversal(node.left,visitor);
preorderTraversal(node.right,visitor);
}
/**
* 中序遍历
*/
public void inorderTraversal(YYBinarySearchTree.Visitor visitor){
if (visitor == null) return;
inorderTraversal(root,visitor);
}
private void inorderTraversal(Node node, YYBinarySearchTree.Visitor visitor){
if (node == null) return;
inorderTraversal(node.left,visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorderTraversal(node.right,visitor);
}
/**
* 后序遍历
*/
public void postorderTraversal(Visitor visitor){
if (visitor == null) return;
postorderTraversal(root,visitor);
}
private void postorderTraversal(Node node, YYBinarySearchTree.Visitor visitor){
if (node == null || visitor.stop) return;
postorderTraversal(node.left,visitor);
postorderTraversal(node.right,visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
/**
* 层序遍历
* visitor --
* @param visitor
*/
public void levelOrderTraversal(YYBinarySearchTree.Visitor visitor){
if (root == null || visitor == null) return;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
//根据外界条件 -- 中止遍历
if (visitor.visit(node.element)) return;
//当前节点的左右子节点入队
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null){
queue.offer(node.right);
}
}
}
/**
* 计算二叉树的高度
* @return
*/
public int height(){
return height(root);
}
public int height(Node node){
if (node == null) return 0;
return 1 + Math.max(height(node.left),height(node.right));
}
/**
* 使用层序遍历 计算二叉树的高度
* @return
*/
public int calHeight(){
if (root == null) return 0;
int height = 0;
//存储着每一层的节点数量
int levelSize = 1;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
levelSize--;
//当前节点的左右子节点入队
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null){
queue.offer(node.right);
}
if (levelSize == 0){//意味着即将要访问下一层
levelSize = queue.size();
height++;
}
}
return height;
}
/**
* 判断是否是完全二叉树
* @return
*/
public boolean isComplete(){
if (root == null) return false;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
boolean isLeaf = false;
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
if (isLeaf && !node.isLeaf()) return false;
if (node.hasTwoNode()){
queue.offer(node.left);
queue.offer(node.right);
}else if (node.left == null && node.right != null){
return false;
}else {//要求后面的节点必须为叶子节点
isLeaf = true;
if (node.left != null){
queue.offer(node.left);
}
}
}
return true;
}
public boolean isCompleteTree(){
if (root == null) return false;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
boolean isLeaf = false;
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
if (isLeaf && !node.isLeaf()) return false;
//当前节点的左右子节点入队
if (node.left != null) {
queue.offer(node.left);
}else if (node.right != null){
return false;
}
if (node.right != null){
queue.offer(node.right);
}else {
isLeaf = true;
}
}
return true;
}
/**
* 返回当前节点的前驱节点
* @param node
* @return
*/
protected Node preNode(Node node){
if (node == null) return null;
Node p = node.left;
if (p != null){
while (p.right != null){
p = p.right;
}
return p;
}
while (node.parent != null && node.parent.left == node){
node = node.parent;
}
return node.parent;
}
/**
* 返回当前节点的后继节点
* @param node
* @return
*/
protected Node succeedNode(Node node){
if (node == null) return null;
Node p = node.right;
if (p != null){
while (p.left != null){
p = p.left;
}
return p;
}
while (node.parent != null && node.parent.right == node){
node = node.parent;
}
return node.parent;
}
public void elementNotNullCheck(E element){
if (element == null){
throw new IllegalArgumentException("element can not is null");
}
}
protected Node createNode(E element,Node parent){
return new Node<>(element,parent);
}
}
-
Node,有left(左子节点),right(右子节点),parent(父节点)三个属性;是节点模型 - 二叉搜索树右root(根节点),comparator(比较器),size(元素数量)三个属性,其中comparator比较器是指节点元素之间的比较规则,是必须要存在的,只有存在比较规则才能确定节点在二叉树中的位置;
- Visitor
是一个抽象类,其提供了在二叉树内部遍历节点元素时的外部处理逻辑,将节点元素传递给外界进行处理; -
public void preorderTraversal(Visitor:前序遍历 -- 递归实现visitor) -
public void inorderTraversal(YYBinarySearchTree.Visitor:中序遍历 -- 递归实现visitor) -
public void postorderTraversal(Visitor:后序遍历 -- 递归实现visitor) -
public void levelOrderTraversal(YYBinarySearchTree.Visitor:层序遍历 -- 迭代+队列实现visitor) -
public int height():使用递归的方式计算二叉树的高度,代码实现如下:
public int height(){
return height(root);
}
public int height(Node node){
if (node == null) return 0;
return 1 + Math.max(height(node.left),height(node.right));
}
- 计算二叉树的高度本质就是
计算根节点的高度,节点的高度是其左右子树高度的最大值;
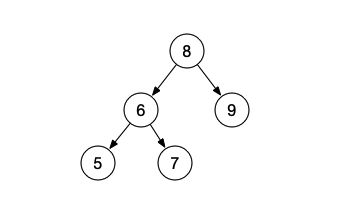
现举例论证,如下图所示的二叉树,利用上述递归计算其高度:
首先传入根节点8即height(8) = 1 + Max(height(6),height(9))
height(6) = 1 + Max(height(5),height(7))
height(5) = 1 + Max(null,null) = 1 + Max(0,0) = 1
height(7) = 1 + Max(null,null) = 1 + Max(0,0) = 1
可以得到 height(6) = 1 + Max(height(5),height(7)) = 1 + Max(1,1) = 2
height(9) = 1 + Max(null,null) = 1 + Max(0,0) = 1
最终得到height(8) = 1 + Max(height(6),height(9)) = 1 + Max(2,1) = 1 + 2 = 3
所以此二叉树的高度height = 3
public int calHeight():使用层序遍历计算二叉树的高度,代码实现如下:
/**
* 使用层序遍历 计算二叉树的高度
* @return
*/
public int calHeight(){
if (root == null) return 0;
int height = 0;
//存储着每一层的节点数量
int levelSize = 1;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
levelSize--;
//当前节点的左右子节点入队
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null){
queue.offer(node.right);
}
if (levelSize == 0){//意味着即将要访问下一层
levelSize = queue.size();
height++;
}
}
return height;
}
我们知道层序遍历,是从上到下,从左到右,一层一层的去遍历二叉树,用变量levelSize记录每一层的节点数量,当当前层的节点出队时,levelSize--,
levelSize == 0时,表明当前层已经遍历完成,马上进入下一层的遍历,这时height+1;循环迭代,最终可得到二叉树的高度。
public boolean isCompleteTree():判断是否为完全二叉树,代码实现如下:
/**
* 判断是否是完全二叉树
* @return
*/
public boolean isCompleteTree(){
if (root == null) return false;
//使用队列 -- Java自带的
Queue> queue = new LinkedList<>();
//根节点入队
queue.offer(root);
//当遇到度为1或0的节点,那么之后的节点必须为叶子节点
boolean needLeaf = false;
while (!queue.isEmpty()){
//队头节点出队
Node node = queue.poll();
if (needLeaf && !node.isLeaf()) return false;
//当前节点的左右子节点入队
if (node.left != null) {
queue.offer(node.left);
}else if (node.right != null){
return false;
}
if (node.right != null){
queue.offer(node.right);
}else {//遇到度为0或1的节点
needLeaf = true;
}
}
return true;
}
- 完全二叉树从上到下,从左到右依次排满,若当前节点出现左节点为空,右节点存在的情况,此二叉树肯定不是完全二叉树;
- 层序遍历二叉树时,若遇到度为0或1的节点,那么之后的节点都是叶子节点,若出现非叶子节点,此二叉树肯定不是完全二叉树。
-
protected Node:获取当前节点的前驱节点,代码实现如下:preNode(Node node)
/**
* 返回当前节点的前驱节点
* @param node
* @return
*/
protected Node preNode(Node node){
if (node == null) return null;
//当node左子节点不为空时,一直获取node的左子节点的右节点,赋值给node,直到node的右节点为空时结束
Node p = node.left;
if (p != null){
while (p.right != null){
p = p.right;
}
return p;
}
//当node左子节点为空且父节点不为空时,即node.left = null && node.parent != null
//一直获取node的父节点,赋值给node,直到node是其父节点的右节点时结束
while (node.parent != null && node.parent.left == node){
node = node.parent;
}
return node.parent;
}
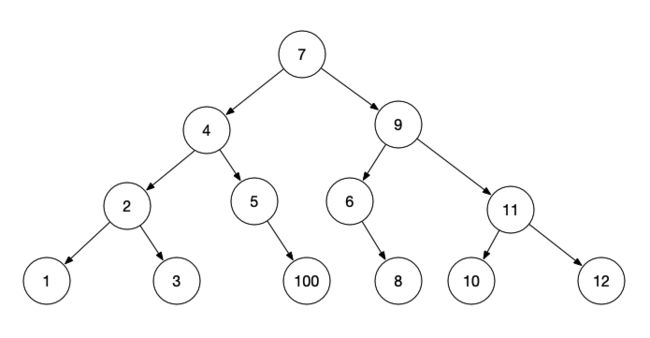
- 举例说明,见下面的二叉树:
易知此二叉树的中序遍历顺序为:1,2,3,4,5,100,7,6,8,9,10,11,12
现在来获取节点7的前驱节点,逻辑如下:
首先节点7的左子节点为4,然后一直取节点4的右子节点,直到右节点为空,最终得到前驱节点为100,完全正确;
再来获取6的前驱节点,逻辑如下:
首先节点6的左子节点为空,父节点为9,node = 6,此时node是父节点9的左子节点,需向上遍历获取9的父节点7,此时将node = 9,node=9是其父节点7的右子节点,遍历结束,最终得到前驱节点为7,完全正确;
protected Node:获取当前节点的后继节点,代码实现如下:succeedNode(Node node)
/**
* 返回当前节点的后继节点
* @param node
* @return
*/
protected Node succeedNode(Node node){
if (node == null) return null;
//当node的右子节点不为空时,不断的去取node的右子节点的左节点,赋值给node;
//直到node为空时截止
Node p = node.right;
if (p != null){
while (p.left != null){
p = p.left;
}
return p;
}
//当node右子节点为空且父节点不为空时,不断的去取node的父节点,并赋值给node
//当node是其父节点parent的左节点时终止
while (node.parent != null && node.parent.right == node){
node = node.parent;
}
return node.parent;
}
- 依然使用上面获取前驱节点的二叉树为例;
- 获取节点100的后继节点,逻辑如下:
- 首先节点100的右子节点为空,父节点为5,由于其node = 100是其父节点5的右子节点,向上遍历,此时让node=5,node=5是其父节点4的右子节点,依然向上遍历,此时让node=4,由于node=4是其父节点7的左子节点,遍历结束,最终后继节点为node.parent = 7;
- 获取节点7的后继节点,逻辑如下:
- 首先节点7的右子节点为9,然后一直取节点9的左子节点,直到左子节点为空,最终获取的后继节点为6,完全正确。