←↑→↓↖↙↗↘↕⏤
unicode=Geometric Shapes
▶ 仅仅个别字不同的时候的对比标识
◆
◉ 着重强调
◆ 1、
◆ 2、
◆ 3、
Miscellaneous Symbols
☞
Dingbats
✍ 重点记忆,个人总结的点,或者知识。
✎✎
⟱
-
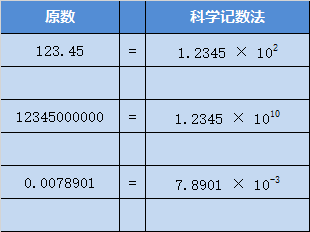
使用科学记数法来表示一个小数
首先来看10进制数如何使用科学记数法来表示:
假设小数的部分,现在只能存储3个10进制数:
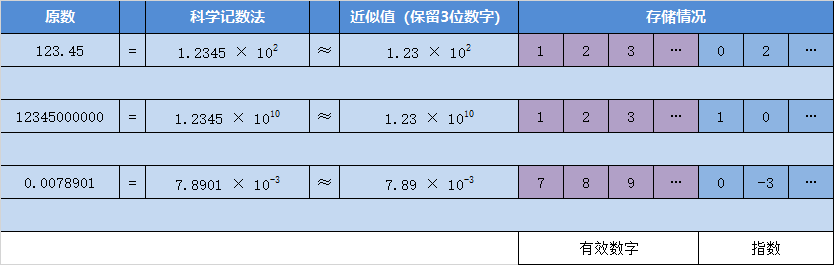
通过上图,可以发现:
1、3个近似值的小数点位置是固定的(在第一个数字之后)
2、指数的底数也是固定的(10)
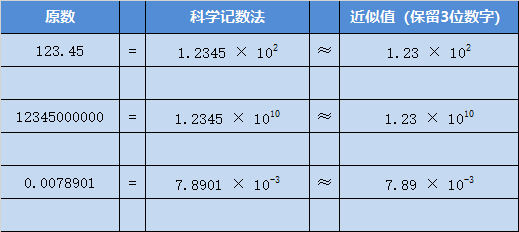
那么,在这个特定的情况下,其实只要知道有效数字的部分,和指数的部分,就可以完全还原这个近似值:
这么做的意义在哪?
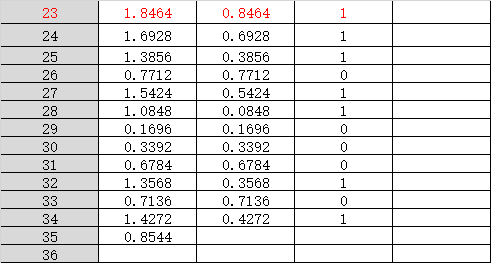
依照上图来说,在保留5个数字的情况下,表示出来的数字范围可从很小到很大(0.0078901-12345000000)。
缺点:不准确,损失了精度。如:
可见,使用这类方法,在精度方面尤其是整数的表示来说,损失是很大的。
-
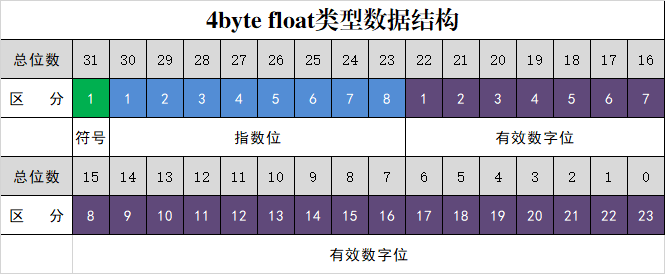
1 程序对浮点数的表示
便于观看,调整格式如下:
-
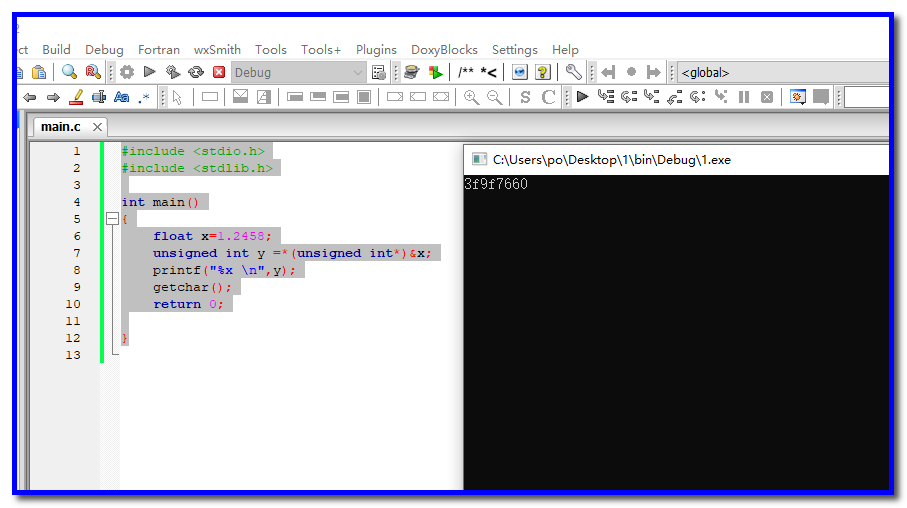
1-1 code::blocks
先看程序计算的结果如何,用作对比:
环境:win10+code::blocks
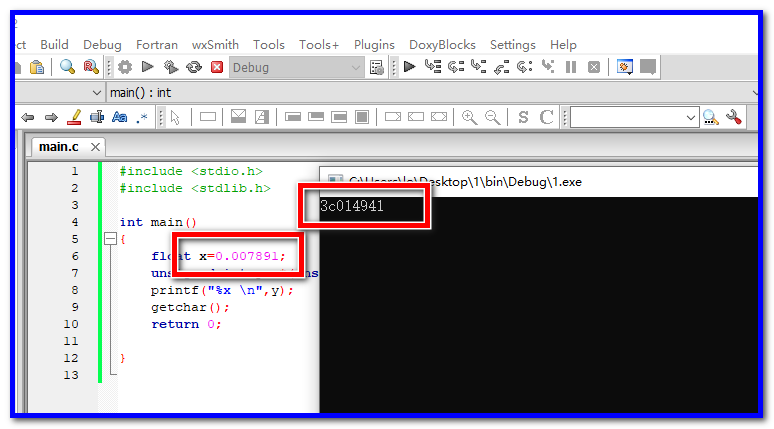
测试数值:float 1.2458
#include
#include
int main()
{
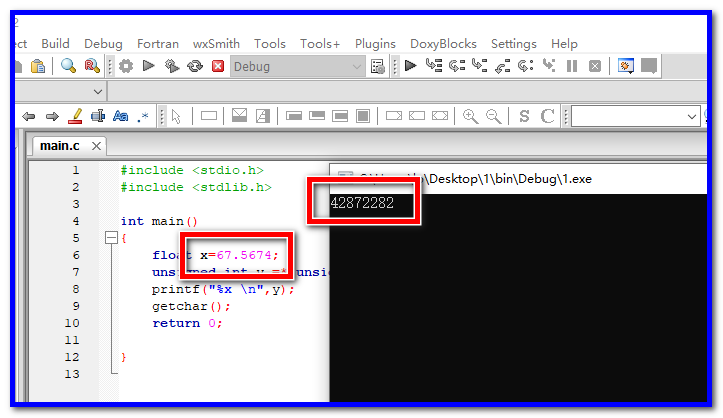
float x=1.2458;
unsigned int y =*(unsigned int*)&x;
printf("%x \n",y);
getchar();
return 0;
}
输出结果:
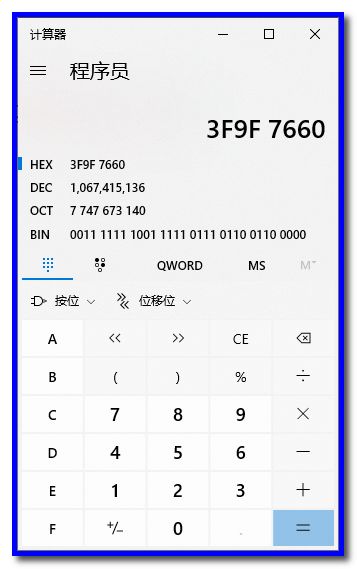
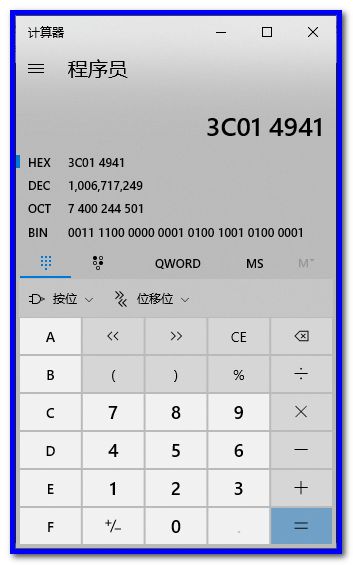
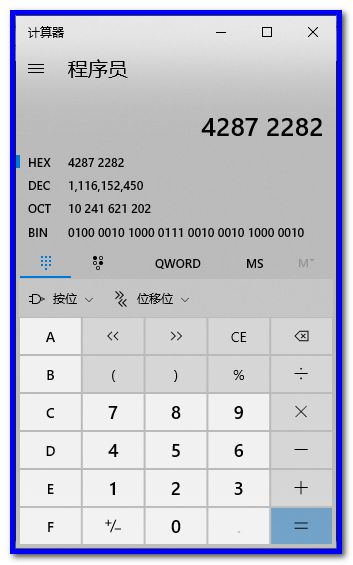
具体值为 3F9F7660。用计算器算一下二进制的值:
把二进制数值复制出来,留作下一步对比使用:
-
1-2 Visual Studio
环境:win10+Visual studio 2013
测试数值:float 1.2458
#include
#include
void main()
{
float x = 1.2458;
printf("%x \n", &x);
getchar();
return 0;
}
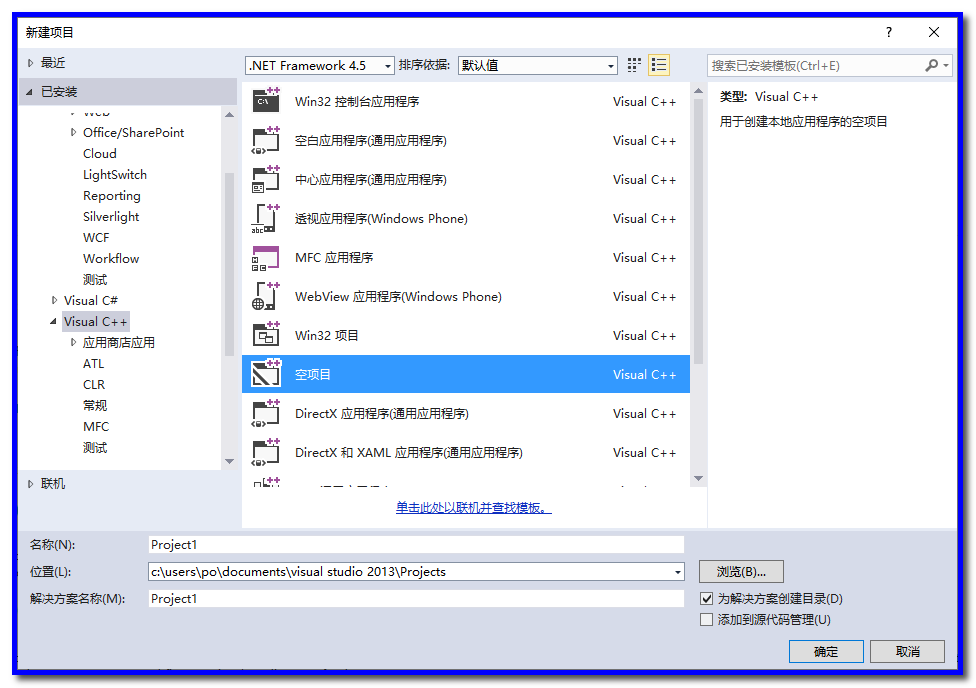
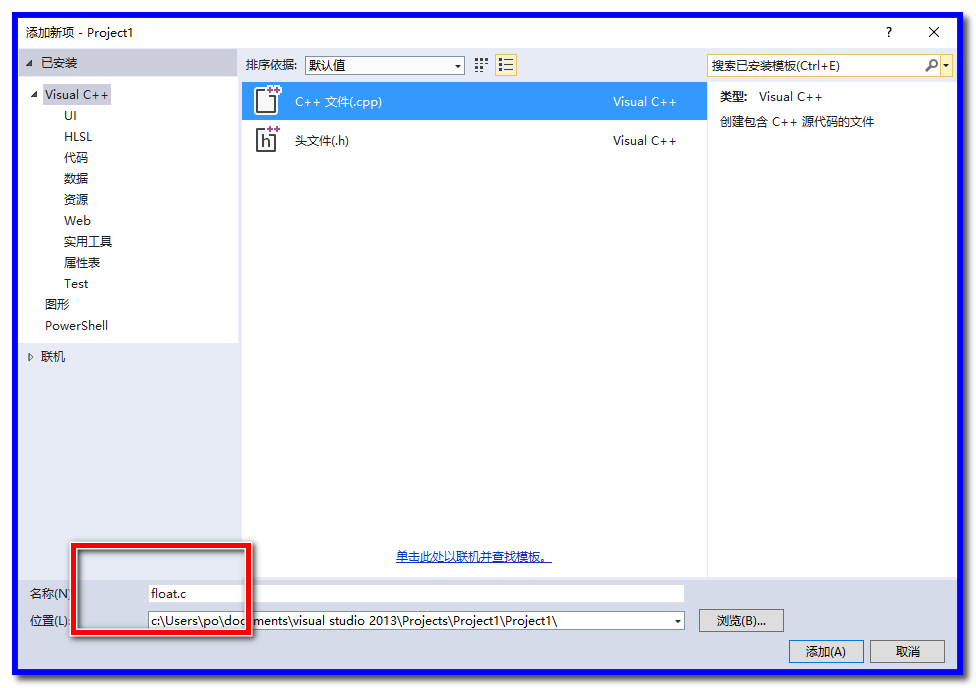
1、新建vc空项目
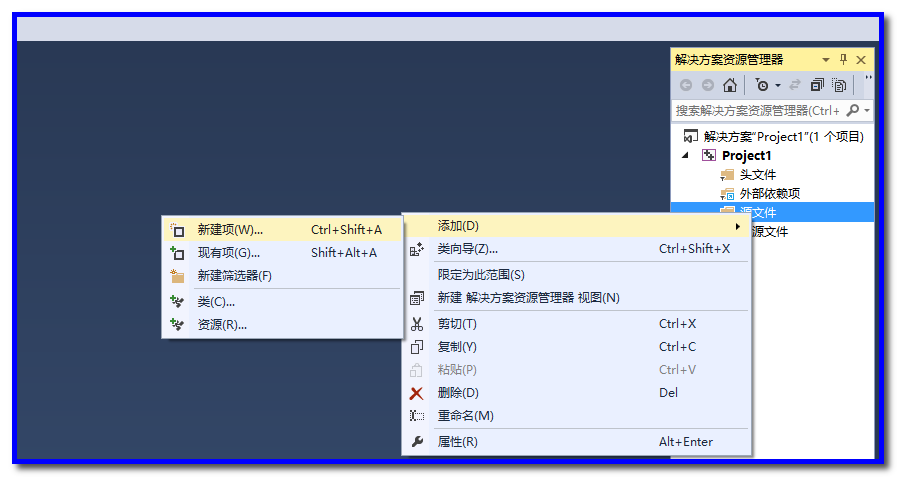
2、添加源文件
3、选择c++文件,并命名
4、打开地址调试(启动内存观测窗口)
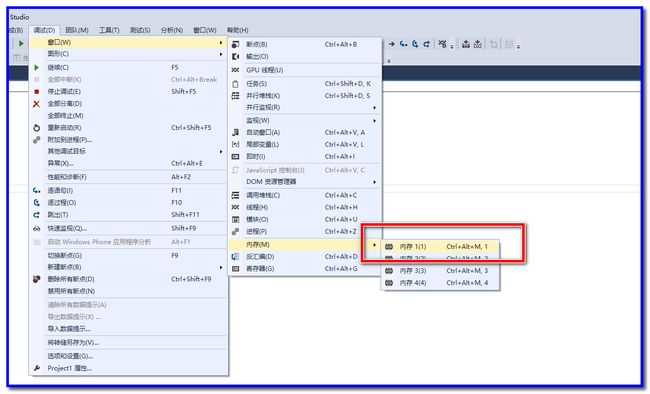
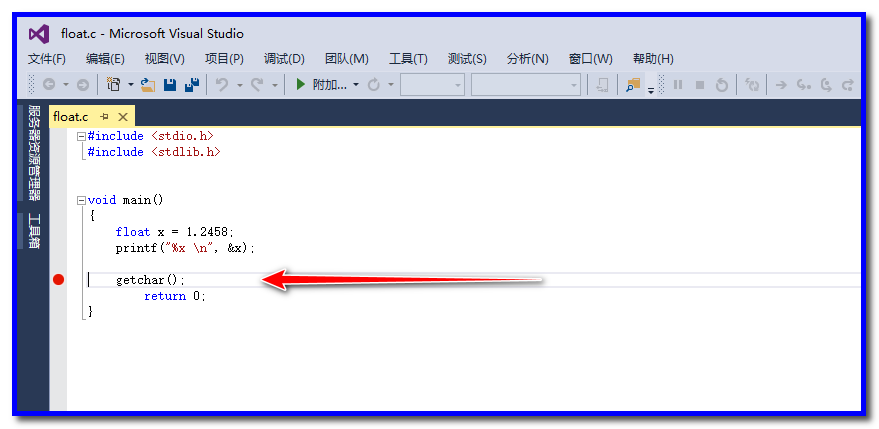
5、在getchar()下断点,让上一句printf能正常输出
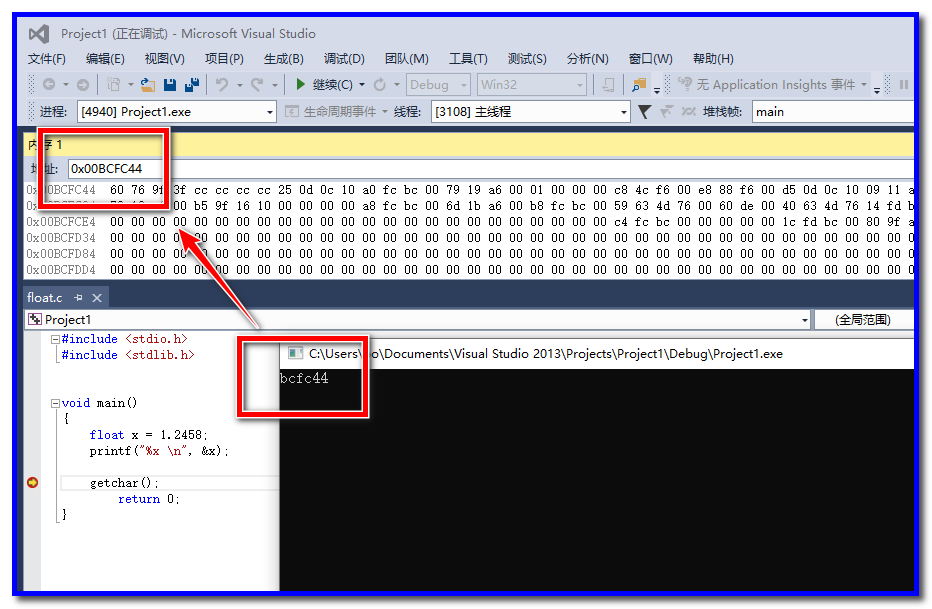
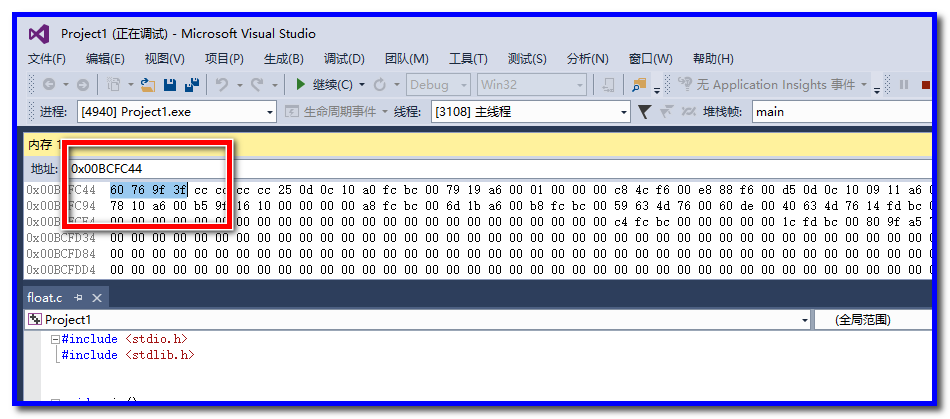
6、启动调试,把x的地址复制到内存窗口中,按下回车查询
7、找到0x00BCFC44处内存的值
因为intel采用的是小端字节序,所以实际的数值应该是3F9F7660,这和code::blocks的输出结果是一致的。
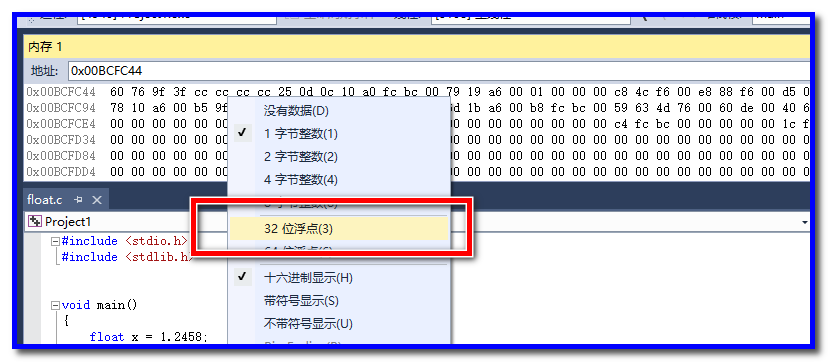
8、在内存窗口右键,选择32位浮点显示
9、可以看到我们定义的浮点数
-
2 10进制小数到2进制小数的转换
方法:
小数部分:乘2取整,顺序排列,直到乘积为0
整数部分:直接转换为2进制
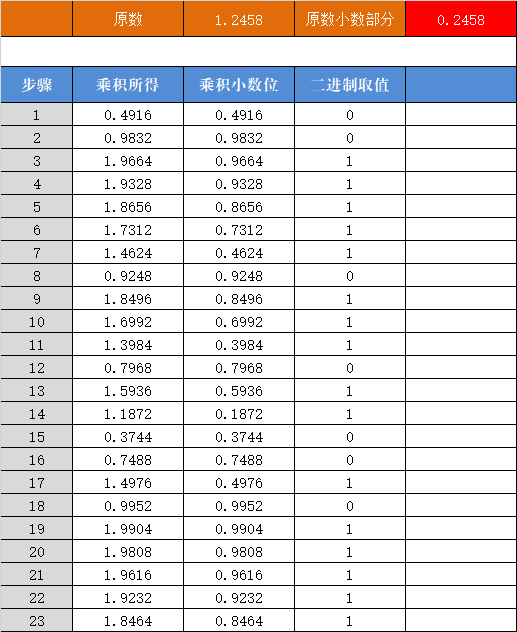
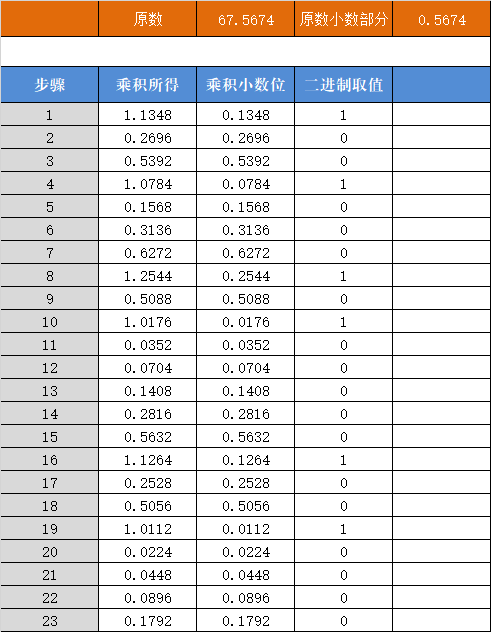
使用文字总是很抽象,下面来看具体分析计算过程。使用excel+vba进行简单计算得出小数部分:
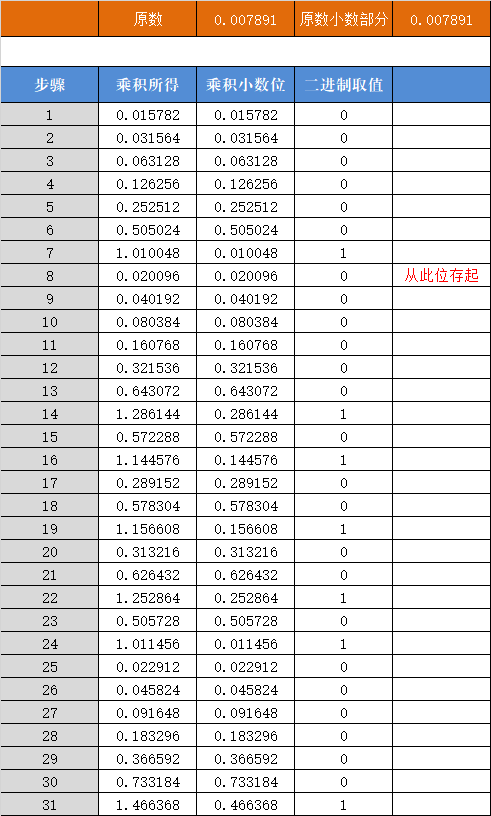
解释:0.2458是上例中1.2458的小数部分。
步骤1后的0.4916是0.2458x2
步骤2后的0.9832是0.4916x2
步骤3后的1.9664是0.9832x2。同时把整数位1放到二进制取值列中,继续用剩下的小数位0.9664参与计算。
以此类推。
因为整数部分为1,所以二进制转换整数部分也是1
所以1.2458的二进制小数应该为:
小数部分的取值,和上上图中的二进制取值列是一致的。
分析到此结束了吗?其实还差一些过程。首先,对比我们计算有效数值部分和程序显示的差异:
上图可以看到,从小数点之后的值,表计算的和程序显示的已经大部分趋同了。那么小数点之前的1去哪里了?
这是因为:浮点数的表示标准里面规定了,有效数值位的第一位必须是1,小数点 . 必须在1之后,这两个要素是约定好了的,所以只用从小数点后开始保存即可。
现在看到上表右起第六列,表计算值为0,程序计算值为1,自此后续的几个数值均不同。这是为什么?
在转换过程中,这个数的小数部分大概率是无穷尽的(没办法乘成一个整数),这样就必须要“四舍五入”。
所以:在计算无穷尽的情况下,看有效位数最后一位的下一位,如果是1,则向前进1。如果是0,则直接丢弃。
所以下面再来对比:
有效值部分已经完全符合。
下面分析指数部分:
由于这个小数的特殊性,正好转化为二进制的时候是:
1.00111110111011001100000
也就是说,这个小数似乎并不需要指数,就能和一个“规范的”二进制小数在形式上符合。
仔细看程序表示的指数部分,它是有值的,7F正好等于127。这又是为什么?
这是因为,这个字段的值等于:二进制小数的指数+127。
这就是说,从这个字段的值来看,二进制小数的指数=0,这正好和我们的分析是一样的。
一个纯小数的例子
先看表格计算的内容:
因为有效数字位不存储0开头的数字,所以实际存储时候从第八行开始。红色1表示要向前进位1位。
但是表的计算值和程序存储的值,是有差异的,具体就是小数点位置不同。为了两者保持一致,程序就必须要存储这个小数点移动的轨迹,也就是程序存储的浮点数的指数部分。程序把小数点向右移动了7位,那么在还原的时候,就要向左移动7位。
也就是说,指数是-7。这和我们使用程序内存表示的数值反推回来的结果是相符的。
一个整数大于1的例子
先看表的计算过程:
再把整数和表计算的小数位结合起来。因为有效数值位必须从1.开始,所有程序保存的数值为黄色部分(24位为0,直接丢弃)。
指数为6,表示在显示(取数据)的时候,小数点要向右移动6位。这是因为在存储的时候小数点向左移动了6位,这样一左一右,取出来的时候就保证了小数点位置的一致。
==================================================================